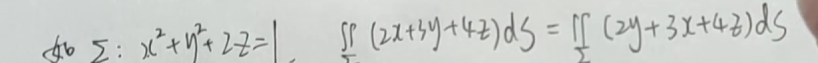临界点。
DP
DP_A AT_arc168_e [ARC168E] Subsegments with Large Sums
对 WQS 二分的理解中很重要的是理解其目的。
我们要对给出的 \(x\) 求 带 \(x\) 的限制的 某个东西的最值 \(f(x)\),但直接求较为困难。于是写成点 \((x,f(x))\),保证所有点 \((x,f(x))\) 形成一个凸壳,用一条斜率为 \(k\) 的直线去切凸壳,在交点(?)\((x,f(x))\) 处满足 \(f(x)=kx+b\),且 \(b\) 是最大/最小值。那么 \(b=f(x)-kx\) 我们不带限制,而是对一些东西的权值 \(-k\),求出 \(b\) 和对应的 \(x\),于是可以求出对应的 \(f(x)\)。但我们这里求出的 \(x\) 可能并不是想要的,于是利用凸性质去(二分)调整斜率,使得直线经过想要的 \(x\)。但不一定会得出 \(x\),不过直线的 \(k,b\) 都定了,自然可以用 \(x\) 在直线上 求出 \(f(x)\)。
总结:直接求点的纵坐标不好求,于是我们用直线信息推出点的纵坐标。
另一种理解:直接理解 \(k\) 对权值的改变,调整了。
恰好划分为 \(k\) 段,感觉二维状态的 DP 没啥前途,尝试使用 WQS 二分。
然而答案 \(f(k)\) 并没有凸性,比如可以先一段平再一段升再一段平。(?)
抓住其他性质,发现可以合并相邻区间,从而得到某种 单调性,从而互换 \(k\) 和 \(f(k)\)。
于是我们先利用答案的单调性(当答案 \(x\) 合法时,\(0\leq x'<x\) 的答案 \(x'\) 也合法),二分答案,判断是否合法。
此时我们又需要处理“恰好”了,再次考虑 WQS 二分。
记当前二分到的答案为 \(x\),那么要求 \(k\in[x,x+(n-len)]\),其中 \(len\) 是权值和 \(\geq s\) 的区间的长度之和。
之前二分的边界保证了 \(x\leq k\),那么现在可行的充要条件是 \(x+(n-len)\geq k\)。
\(n-k\) 是定值,现在要求恰好有 \(x\) 个 \(\geq s\) 的段的情况下,\(\sum(r-l)\) 最小。
注意到 \(\min \{ \sum (r-l) \}\)(自变量是 \(x\))是下凸的。(?)
感性理解:先选小区间。(?)
这样就可以 WQS 二分了,里面写一个 DP 来求这个 \(\min\) 即可。
DP 数组有二:\(f_i\) 表示前 \(i\) 个数的 \(\min{\sum(r-l-mid)}\),而 \(seg_i\) 表示 此时 最小的 \(x\)(这个最小使得斜率能够取到我们想要的(?),具体见代码,尤其是其中二分里判断的部分)。
具体转移见代码。
\(f\) 的写法可能导致和定义不同,不知道会不会不行。(?)
注意 \(\sum\) 里的不是所有段,而是 \(\geq s\) 的段。
时间复杂度为 \(O(n\log k\log n)\)。
有单 \(\log\) 做法,大概是合并两个二分,然后在直线上按顺序枚举点?见洛谷题解区,why 似乎也是写的这个做法。
具体写法和参考资料见代码。
DP_B CF1930G Prefix Max Set Counting
统计本质不同前缀最大值序列数,不需要关注方案数或每种方案,只需要关注每个前缀最大值序列是否出现,于是我们对每个前缀最大值序列,都尽量构造它出现的情况。
设 \(f_i\) 表示以 \(i\) 结尾的方案数,由 \(f_j\) 转移到 \(f_i\),表示 \(j,i\) 在前缀最大值序列上相邻。
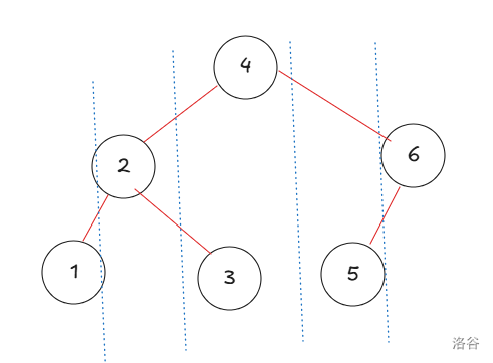
题目说的就是 DFS 序。另有一个关键观察:走过一个点就必须紧接着走完它的子树,这里对之后限制最严的是它的子树 \(\max\)。
画图分讨,仅考虑有用的点。丢进树状数组里,树状数组优化。
具体写法和参考资料见代码。
DP_F CF1874F Jellyfish and OEIS
极其困难!有一种《主旋律》(一道题)的美(细致考虑 DP 的过程中如何转移,用到未完成的 DP 值来转移)。
容斥,钦定不合法区间(只考虑被限制的区间),设钦定的区间构成的集合为 \(S\),则容斥系数是 \((-1)^{|S|}\)。尝试将容斥系数融入 DP。区间杂乱不好处理,尝试干掉相交但不包含的区间,变成类似树的结构(但好像不完全是)。
考虑相交的钦定区间,发现中间的相交部分一定也可被钦定,且如果钦定了两个大区间,它就会自然被钦定。于是此时它是否被钦定并不影响方案数,只会使容斥系数乘 \((-1)\),那么贡献(容斥系数乘对应方案数之和)就被抵消为 \(0\)。
于是干掉了相交但不包含的区间。现在得到类似树的结构,可以区间 DP 了。
设 \(f_{l,r}\) 为只考虑 \([l,r]\) 时的贡献之和(且不能钦定 \([l,r]\),即 \([l,r]\notin S\))。(\([l,r]\))
我们考量结构,发现一个大区间应该拆成若干个被钦定区间覆盖的子区间(再把它们拆成若干个钦定区间,当然每个钦定区间内可能还有其他更小的钦定区间),和若干未被钦定区间覆盖的点(称为“自由元”)。显然自由元可以自由地排列,它们的贡献就是自由元个数的阶乘。而对于钦定的区间,我们把它的贡献算好拿上来用。
于是从左往右填这个当前的大区间,类似背包,设 \(g_{l,r,i}\)(固定 \(l\))表示 “大区间” \([l,r]\) 中有 \(i\) 个自由元的贡献之和,用以辅助 \(f\) 的转移。\(g\) 的转移分两种情况(注意是 \(+=\) 而非 \(=\)):
- 填一个自由元:\(g_{l,r,i}+=g_{l,r-1,i-1}\)。初值是 \(g_{l,l-1,0}=1,g_{l,l-1,others}=0\)。
- 填一个钦定区间:\(g_{l,r,i}+=-\sum_{j=l+1}^{r}g_{l,j-1,i}\cdot f_{j,r}\)。
- 根据 \(f\) 的定义,\(f_{j,r}\) 原先并未钦定,于是 \(f_{j,r}\) 要在现在钦定,那么容斥系数会多乘一个 \((-1)\),于是有 \(-\)。
- 事实上还要添加 \(j=l\) 的情况,即整个区间都被钦定,此时要给 \(g_{l,r,0}\) 加上 \(-f_{l,r}\)(可以用之前的式子,结合 \(g_{l,l-1,0}=1,g_{l,l-1,others}=0\))。但是这里要先用 \(g_{l,r,i}\) 更新 \(f_{l,r}\),而 \(f_{l,r}\) 不允许钦定 \([l,r]\),于是应该先用上面的式子得到的 \(g_{l,r,i}\) 更新 \(f_{l,r}\),再用 \(f_{l,r}\) 更新 \(g_{l,r,0}\)。这样也不会产生转移形成环的问题。
- 很需要注意的一点:填一个钦定区间的两种转移(\(f\) 前,\(f\) 后)都要求式子里 \(f_{x,y}\) 的 \([x,y]\) 可以钦定,即 \(x \leq y \leq m_x\)。
从 \(g\) 转移到 \(f\):
于是我们从外到内第 \(1\) 层从大到小枚举 \(l\),第 \(2\) 层从小到大枚举 \(r\),第 \(3\) 层从小到大枚举 \(i\),第 \(4\) 层枚举 \(j\) 即可转移。
最后的答案,若 \([1,n]\) 可被钦定,即 \(m_1=n\),那就相当于要求整个排列不是排列,显然答案为 \(0\);否则 \([1,n]\) 不可被钦定,此时 \(f_{1,n}\) 就没有钦定 \([1,n]\),直接就是答案。
预处理阶乘。
时间复杂度貌似是 \(O(n^4)\),但似乎常数很小,或者 CF 机子快?
具体写法和参考资料见代码。
2025.3.24