E1. Canteen (Easy Version)E2 Cantee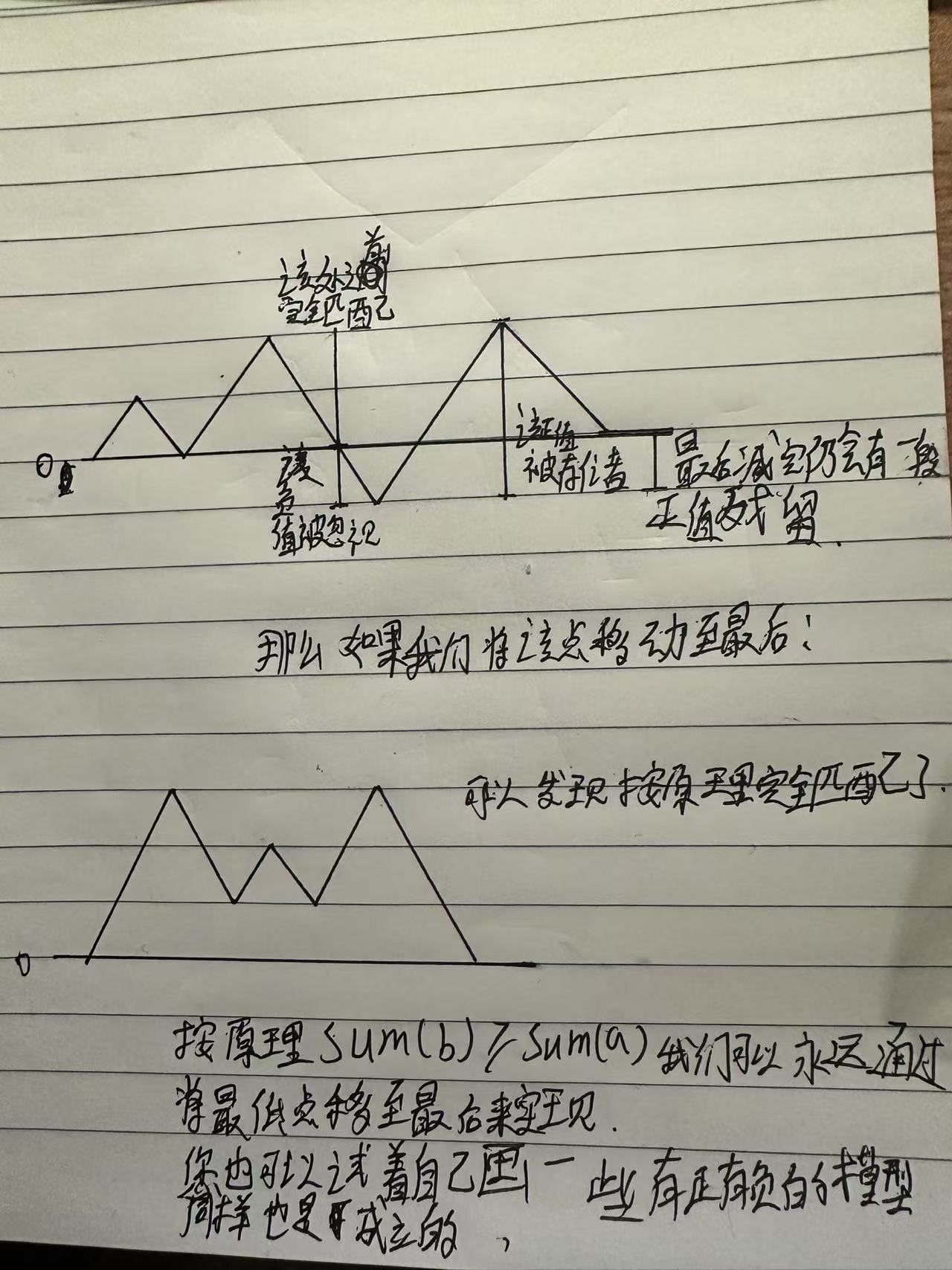n (Hard Version) 对于旋转操作的深入理解

E1. Canteen (Easy Version) 题解：二分查找 + 模拟

本文大量学习了jiangly的代码对其进行详细的解析并作图对其进行解释

题目链接

深入解析：前缀和最小值旋转的直观意义

---

一、前缀和曲线的数学本质

我们定义前缀和数组为：

pre[i+1] = pre[i] + a[i] - b[i]

这一公式的物理意义是：从起点到位置 i 的累积过程中，a 的总和比 b 少多少（若为负值，则说明 b 的总和超过 a）。
例如，假设 a = [1, 2, 3]，b = [4, 1, 4]，则前缀和为：

pre = [0, 0+1-4=-3, -3+2-1=-2, -2+3-4=-3]

此时 pre[1]=-3 是前缀和的最小值。

---

二、为何旋转到最小值位置？

通过循环左移，将前缀和的最小值位置 x 设为新起点，本质是将 b 的累积优势最大化区间对齐到数组开头。
以下通过图像化示例说明：

1. 前缀和曲线示意图

假设前缀和曲线形状如下（横轴为索引，纵轴为 pre[i]）：

pre: 0 → -3 → -5 → -2 → 0  (最小值在索引2)

• 负值区域：表示 b 的累积优势区（b 总和显著超过 a）。
• 正值区域：表示 a 的累积过剩区（需后续处理）。

2. 旋转后的效果

将最小值位置 x=2 设为新起点，前缀和曲线变为：

新 pre: -5 → -2 → 0 → -3 → 0

此时，曲线从最小值开始逐步上升，后续的 b 元素（如索引3的 b[3]=4）可以更高效地处理积压的 a 元素。

---

三、栈模拟与贪心抵消的直观演示

1. 栈的作用

栈中存储的是未被抵消的 a 元素的索引。例如：

• 初始时 a = [3,4,1,2]，b = [2,1,4,3]（旋转后）。
• 处理 b[2]=4 时，栈顶的 a[0]=3 和 a[1]=4 可被快速抵消。

2. 时间窗口限制

假设允许轮数 mid=2：

• 若当前处理到 i=2，栈顶元素 j=0，则 i-j=2 满足条件。
• b[2]=4 可抵消 a[0] 和 a[1]，无需计入 k 操作。

---

四、为何“正值累加不超过最小负值差”？

1. 数学原理
   前缀和的最小值为 pre_min，最终 pre[n]=0（因 sum(a) ≤ sum(b)）。
   从 pre_min 到 pre[n] 的累加为 -pre_min，即所有正值区域的累加不超过 -pre_min。
   物理意义：b 的累积优势足以覆盖所有 a 的过剩部分。

2. 图像验证
   从前缀和最小值开始，曲线逐步上升至终点。上升部分的累加值（正值区域）必然被初始的负值深度（pre_min）所限制。

---

五、动手画图理解

1. 步骤示例

   • 画横轴为索引，纵轴为 pre[i]。
   • 标记最小值点 x，旋转后曲线从 x 开始。
   • 观察旋转后的曲线是否满足“上升段总和 ≤ |pre_min|”。

2. 实例验证
   以样例输入中的第六个测试用例为例：

   a = [1,2,3,4], b = [4,3,2,1]
   pre = [0, -3, -4, -3, 0]
   

   旋转到 x=2 后，a 和 b 变为：

   a = [3,4,1,2], b = [2,1,4,3]
   

   此时 b[2]=4 和 b[3]=3 能高效处理栈中积压的 a 元素，减少轮数。

---

#include<bits/stdc++.h>
#define int long long
#define all(x) x.begin(),x.end()
#define rall(x) x.rbegin(),x.rend()
#define pb push_back
#define pii pair<int,int>
using namespace std;
const int mod=998244353;
int gcd(int a,int b){return b?gcd(b,a%b):a;};
int qpw(int a,int b){int ans=1;while(b){if(b&1)ans=ans*a%mod;a=a*a%mod,b>>=1;}return ans;}
int inv(int x){return qpw(x,mod-2);}
void solve(){int n,k; cin>>n>>k;vector<int>a(n),b(n);for (int i=0;i<n;i++)cin>>a[i];for (int i=0;i<n;i++)cin>>b[i];vector<int>pre(n+1);for (int i=0;i<n;i++) {pre[i+1]=pre[i]+a[i]-b[i];//因为题目中指出sum(b)>=sum(a)所以我们需要计算这个b的前缀-a的前缀的最大点 将其作为旋转使其可以实现完全匹配}// 可能有同学会不太理解为什么把b前缀减去a前缀的最大移动到最后就一定能够实现完全匹配 因为我们要实现一个类似于栈的移动匹配// 我们把优先b能够实现匹配的数放到前面这样栈里面就能够存储未实现匹配的a// 把匹配的压力优先放到后面 访问到后面的b时能够最大限度地对前面地a进行删除// 如果还是太过抽象 那么我们可以将其想象成一边是单调下降一边是单调上升的曲线// 对于曲线上升为正数的部分我们会进行保留即为被保存在栈中 为负数的部分我们会忽略// 那么见图可以得知该结论是正确的 具体原理为直线的正值累加是不可能超过最小负值点的差// 您也可以自己画着试试{int x=ranges::min_element(pre)-pre.begin();rotate(a.begin(),a.begin()+x,a.end());rotate(b.begin(),b.begin()+x,b.end());}vector<int>na,nb;auto check=[&](int x) {na=a,nb=b;int sum=0;stack<int>stk;for (int i=0;i<n;i++) {stk.push(i);while (!stk.empty()&&nb[i]>0) {int j=stk.top();if (i-j>=x) {sum+=na[j];stk.pop();}else {int t=min(na[j],nb[i]);na[j]-=t;nb[i]-=t;if (na[j]==0) {stk.pop();}}}}return sum<=k;};int l=0,r=n;int ans=0;while (l<=r) {int mid=(l+r)>>1;if (check(mid)) {ans=mid;r=mid-1;}else l=mid+1;}cout<<ans<<endl;
}
signed main(){ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr);int _=1;cin>>_;while(_--)solve();
}