二分图学习笔记

使用题单：二分图 - 从入门到入土。

二分图概念

对于一个图，如果能够把它的点集恰好分成两个部分，使得这第一个部分里面的点两两不连边，第二个部分里面的点也两两不连边，则该图是二分图。或者说每一条边都横跨了两个集合。

举个例子：

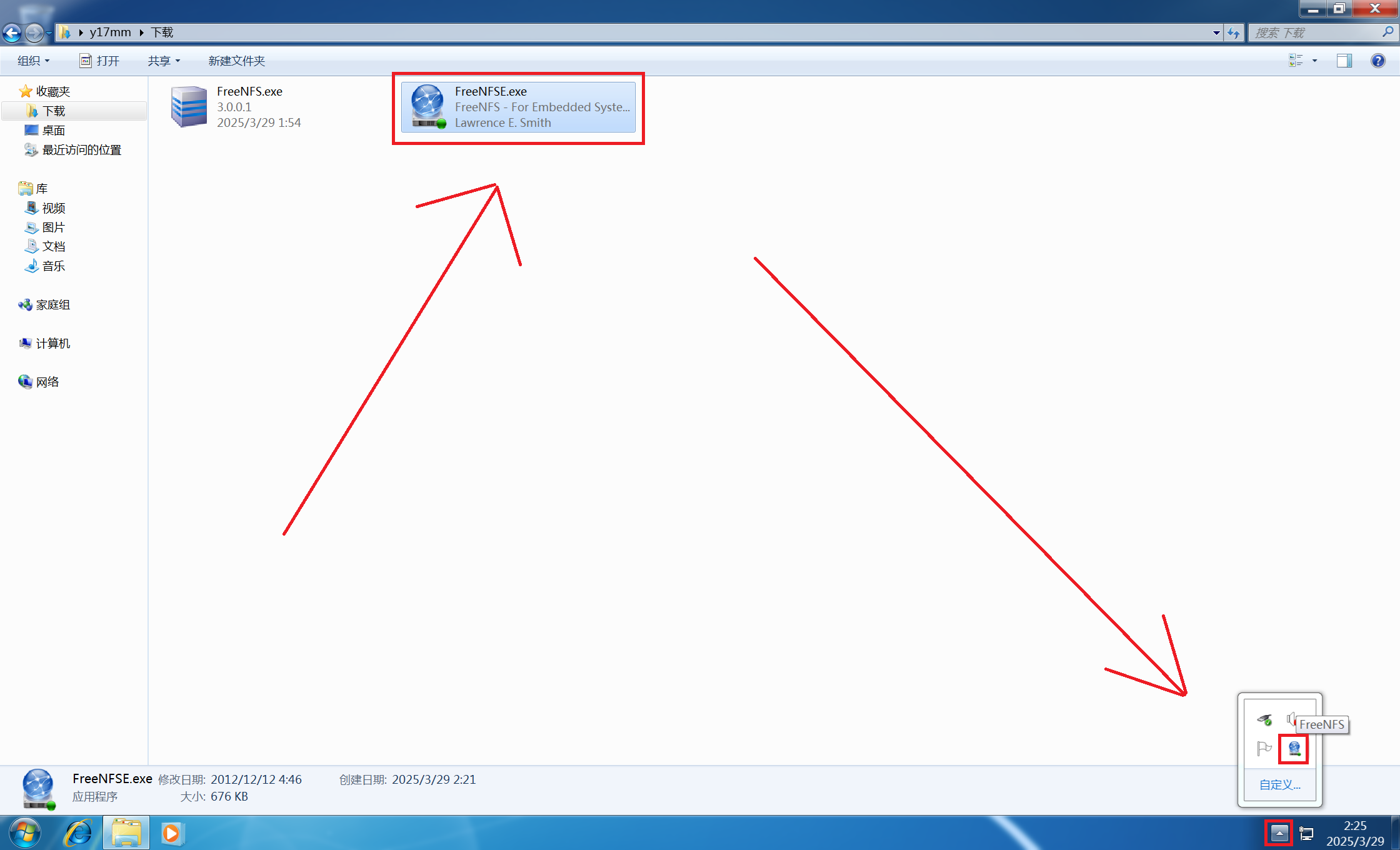
这个图是二分图，因为我们可以将它分成 \(\{1,3,5,7\}\) 和 \(\{2,4,6\}\) 两个点集：

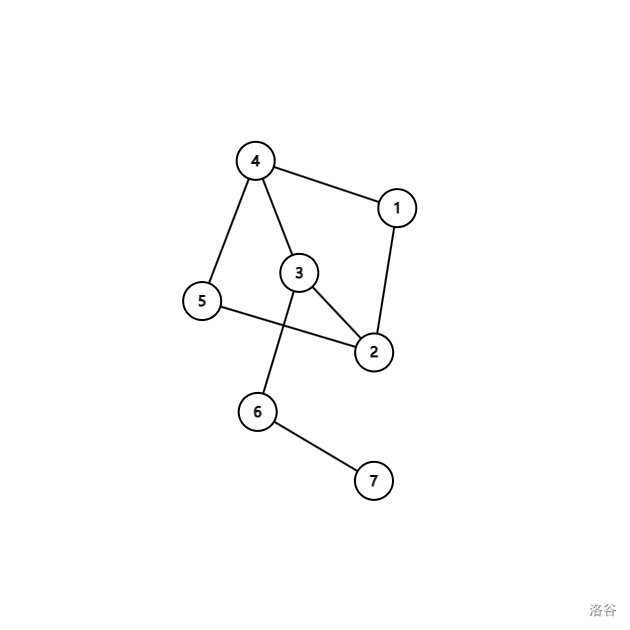
但是这个图：

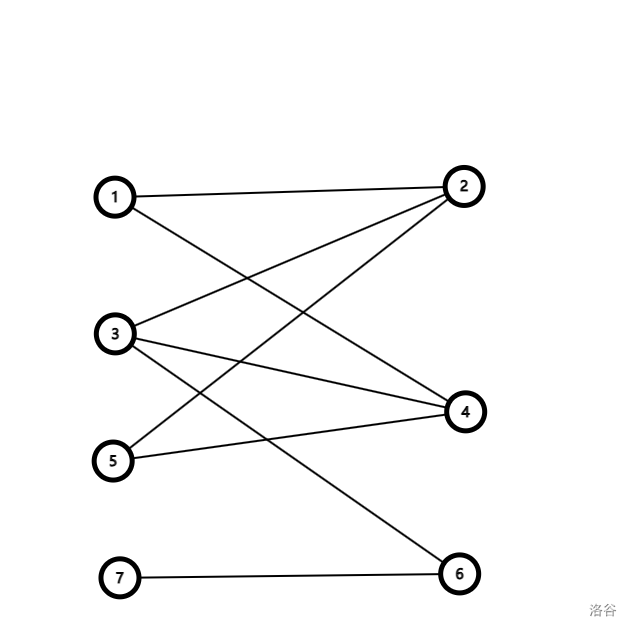
可以发现这个图无论如何也无法划分点集，所以这个图不是二分图。

还是给一下不说人话的形式化定义：

二分图：如果一张无向图 \((V,E)\) 存在点集 \(A,B\)，满足 \(|A|,|B| \ge 1\)，\(A \cap B = \emptyset\)，\(A \cup B = V\)，且对于任意 \(x,y \in A\) 或 \(x,y \in B\)，\((x,y) \not \in E\)，则称这张无向图为二分图，\(A,B\) 分别称为二分图的左部和右部。

注意，二分图可以不是连通图。

二分图判定

很容易想到一个小学奥数的知识：黑白染色。黑白染色之后若没有冲突的边则就是二分图。

黑白染色就是先任意指定一个点的颜色，然后对于每一条边，都要使两个端点的颜色不同（对应所属于的点集不同），所以每走一条边就变一下颜色。

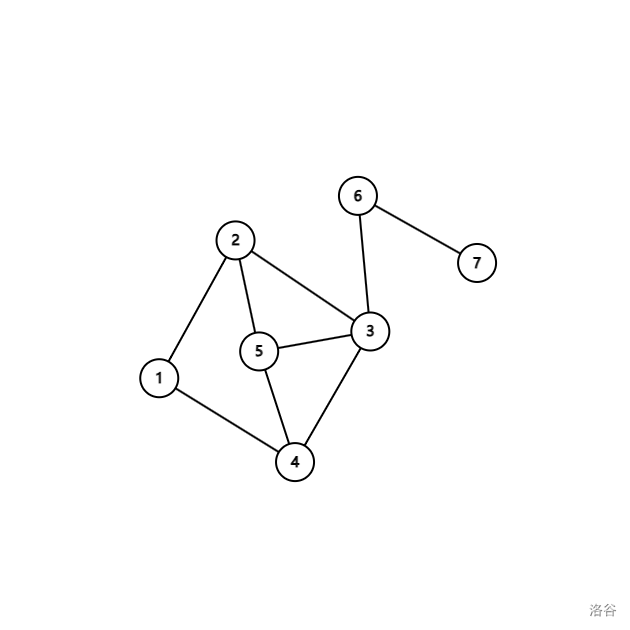
例如文章自上而下的第一个图黑白染色之后得到：

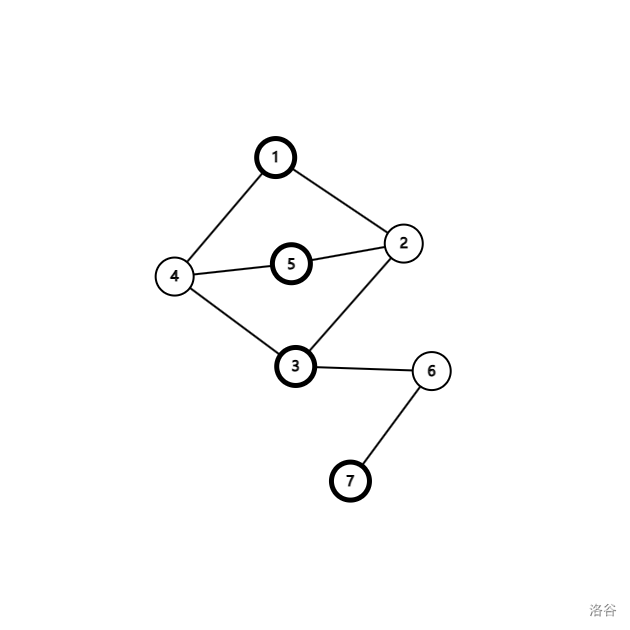
冲突的意思就是一条边的两个端点的颜色相同。因为在同一条边上面，所以这两个点不能在同一个点集。因为这两个点是因为其他边被迫的颜色相同，所以这两个点又不得不在同一个点集里面（如果不在又会发生其他问题）。所以矛盾，所以有冲突的边的图不是二分图。

别急，我们先不立即学二分图匹配，先来看一道题。

CF862B Mahmoud and Ehab and the bipartiteness

题意就是给定一棵树，求至多添加多少条边使得二分图的性质仍然成立。

显然对于这棵树染色，就可以得出无论加多少边二分图的点集一定是什么样子（如果不是这个样子就违背了最基本的树的条件）。

为了最大化边的数量，一定要让左右部尽可能地交叉连边。算出边的数量之后再减去 \(n-1\) 即可。

答案：\(左部点数量 \times 右部点数量 - (n-1)\)。

可以证明，这个值一定不小于 \(0\)。读者可以自己尝试证明一下。

二分图匹配

匹配的定义：在二分图中找到一些边，使得边与边之间没有公共点，那么这组边就是二分图的一种匹配。