4.1 CW 模拟赛 T1. 棋子

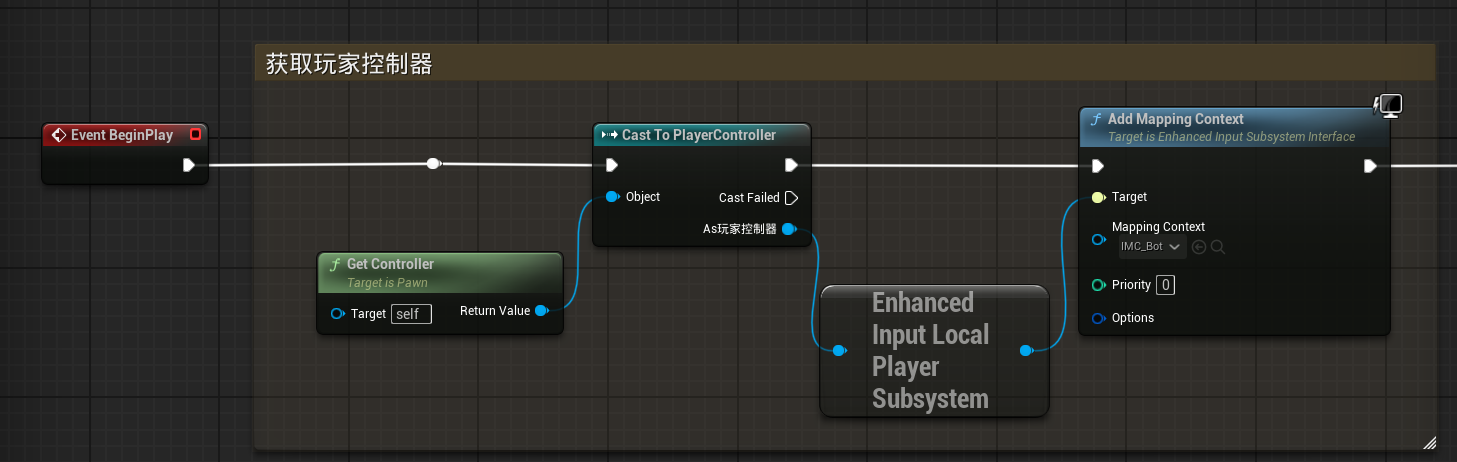
前言

赛时似乎一堆人都是猜的, 证明并不是显然的东西, 好好搞

思路

套路

• 概率与期望
  • 加法与乘法的结合本质上是穷举所有可能的独立组合
  • $\rm{dp}$ 特殊的点
    • 一定一定一定要分阶段
    • 可以先讨论那些更特殊的元素, 作为前阶段, 也就是说, 你可以在不影响概率的前提下处理阶段的优先级
    • 注意即使要求取 $\max, \min$, 也可以通过 $\rm{dp}$ 来处理, 实质即为通过改变操作序列来最值化一些东西, 不是真的对概率和期望进行取最值
  • 结束状态一定倒推, 开始状态一定正推
    • 按照规模 $\rm{dp}$
  • 期望 $\rm{dp}$
    • 全期望公式直接转移
    • 用期望定义
      • 可以求出每种情况的方案数，然后用期望定义得到答案
      • 先概率 $\rm{dp}$
    • 期望的线性性拆开考虑
    • 整体等概率一般可以拆成每一次均匀选择

首先第一次直接 \(\rm{win}\) 了是 \(\dfrac{1}{n}\), 其他 \(\dfrac{n - 1}{n}\) 次显然再也不会回到起点或者回到起点之前了
那么拆成两部分
第一部分是 \(1\) 次

设后面再用 \(k\) 次, 计算 \(k\) 的期望
显然 \(k = 0\) 概率为 \(\dfrac{1}{n}\)

不难发现在要么 \(\dfrac{1}{n - 1}\) 的概率下结束, 要么在 \(\dfrac{n - 2}{n - 1}\) 的概率下进入下一轮, 不考虑那一种再来一次的贡献
设当前轮结束的期望步数为 \(e\), 不难发现进入下一轮仍然是 \(e\)

\[e = \dfrac{1}{n - 1} \times 1 + \dfrac{n - 2}{n - 1} \times (e + 1) \]

解得 \(e = n - 1\)

因此 \(E(k) = \dfrac{1}{n} \times 0 + \dfrac{n - 1}{n} \times e = \dfrac{(n - 1)^2}{n}\)

总的步数 \(E(k + 1) = \dfrac{(n - 1)^2}{n} + 1\)

总结

比较猎奇的做法, 关键在于发现

从 \(1\) 号格到 \(n-1\) 号格花费 \(1\) 的代价进入终点的期望是相同的, 都是 \(\frac{1}{n-1}\), 另外 \(\frac{n-2}{n-1}\) 的概率继续停留在 \(1 \sim n-1\) 号格内, 故在这个问题上, 位于 \(1\sim n-1\) 号格子上的状态都是等价的

一种到达和不到达概率完全一样, 且不到达之后到达和不到达概率同样和之前完全一样的完全一样的特解, 也即直接视为一样的状态

\(\textrm{Thanks to }\)\(\textrm{the author}\)\(\textrm{ for the idea.}\)