Day 15
01. 翻转二叉树(No. 226)
题目链接
代码随想录题解
1.1 题目
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
示例 1:
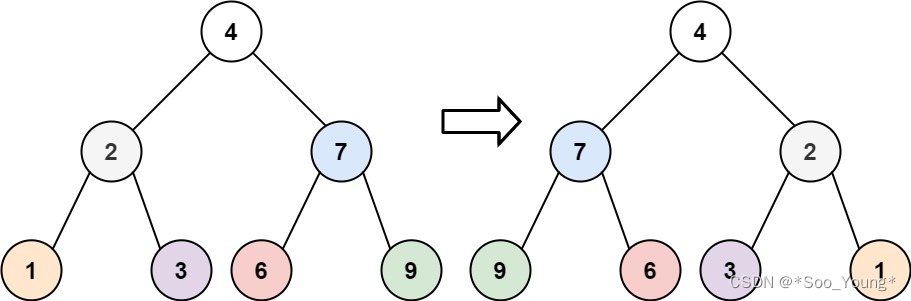
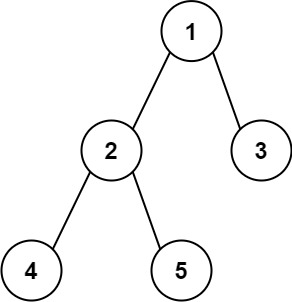
输入:root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]
示例 2:
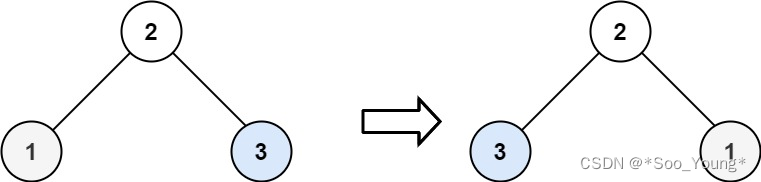
输入:root = [2,1,3]
输出:[2,3,1]
示例 3:
输入:root = []
输出:[]
提示:
- 树中节点数目范围在
[0, 100]内 -100 <= Node.val <= 100
1.2 笔记
一道考察递归遍历的题目,我们要先理清这道题目的要求
题目要求我们的是交换二叉树的节点,注意不是交换值,所以我们要在递归遍历的时候去交换节点,递归遍历分为前序、中序和后序,我们只需要在遍历到节点的期间去交换节点即可。
下面我们以前序为例子:

和上面提到的相同,前序遍历就是在进入节点的时候立刻进行的操作,我们在进入节点前交换左右子树,和上一节博客讲的一样,对所有的节点进行相同的处理,即可完成交换
后序遍历也是同理。
但是中序遍历是不行的,中序遍历是在左子树返回的时候进行交换,我们看看会有什么后果:
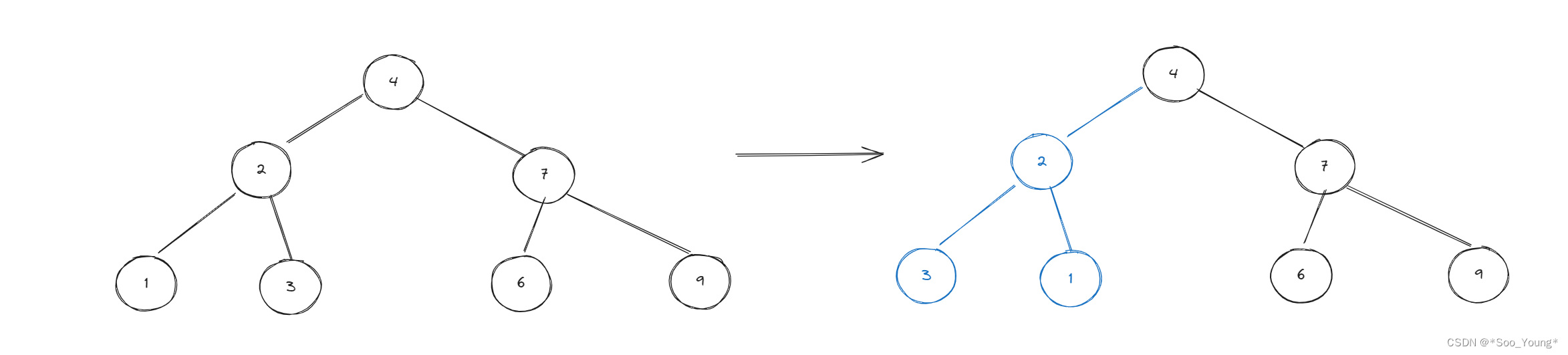
比如我们这里把左子树处理完了
这时候我们中序回到根节点,将 2 和 7 一交换再去递归右边,这不是就完全恢复了吗?
就相当于我们只交换了根节点下面的两个节点,其他是没变化的
写到这里就可以给出代码了
1.3 代码
class Solution {public TreeNode invertTree(TreeNode root) {traverse(root);return root;}public void traverse(TreeNode root) {// 递归出口if (root == null) {return;}// 交换节点TreeNode temp = root.left;root.left = root.right;root.right = temp;traverse(root.left);traverse(root.right);}
}
02. 对称二叉树(No. 101)
题目链接
代码随想录题解
2.1 题目
给你一个二叉树的根节点 root , 检查它是否轴对称。
示例 1:
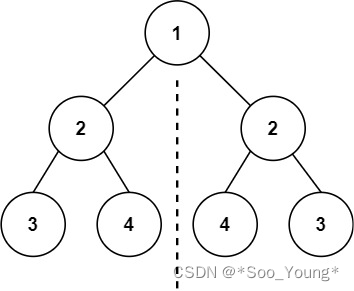
输入:root = [1,2,2,3,4,4,3]
输出:true
示例 2:
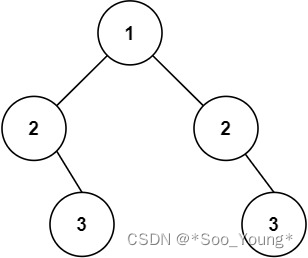
输入:root = [1,2,2,null,3,null,3]
输出:false
提示:
- 树中节点数目在范围
[1, 1000]内 -100 <= Node.val <= 100
2.2 笔记
这道题我们要理解后序遍历的特殊性,后序遍历是在遍历完子节点后返回时做的操作,这就意味着我们可以 收集到子节点的信息,所以后序遍历经常用在需要子节点信息的情况。
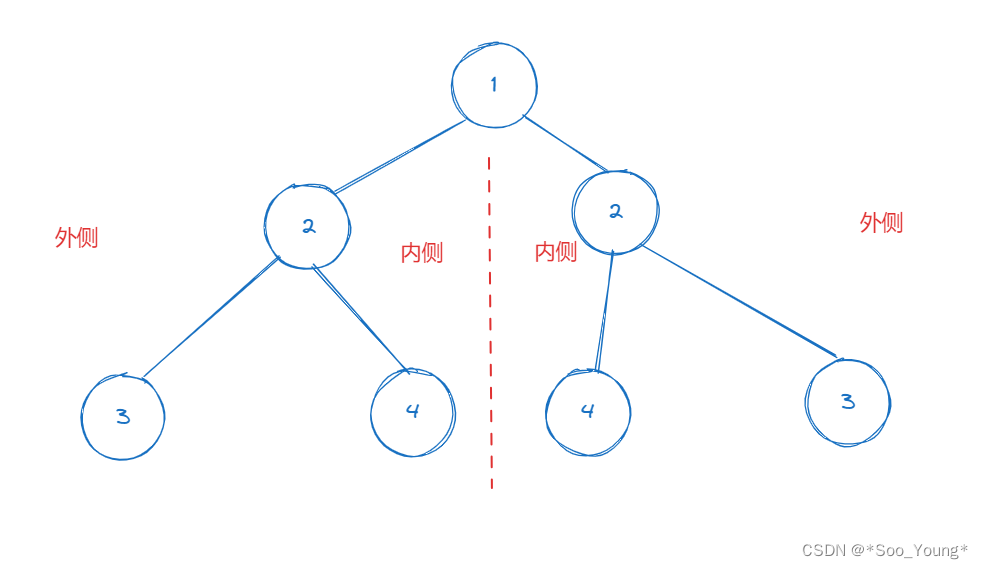
这道题我们要比较内侧和外侧的信息,我们如何遍历这个树的外侧呢?
回顾一下我们写的二叉树遍历的代码:
public void reverse(TreeNode node) {reverse(node.right);reverse(node.left);
}
我们对每个节点进行的操作是遍历 左子树 和 右子树,但如果我们要求的只是遍历外侧,也就是说只遍历 左节点的左节点和右节点的右节点:
public void reverse(Treenode right) {reverse(node.right);
}
和
public void reverse(Treenode left) {reverse(node.left);
}
这便是遍历树的外侧,抛去二叉树的外壳,这其实就是链表的递归遍历
接下来我们将这两个方向的遍历合在一起
public boolean isSymmetric(TreeNode root) {return compare(root.left, root.right);}public boolean compare(TreeNode left, TreeNode right) {if (left == null && right != null) {return false;}if (right == null && left != null) {return false;}if (right == null && left == null) {return true;}if (right.val != left.val) {return false;}boolean compareOutside = compare(left.left, right.right);return compareOutside;
}
上述的代码就是将根节点的左右节点分别传入,对左节点只进行向左的递归,对右节点只进行向右的递归,注意我们返回结果的位置正是说的后序的位置,因为只有这个位置才是验证完成 子节点 的对称性并且返回的的位置。
这个位置可以理解为我们 收集信息 的位置,如果对理解递归有困难的话,我们可以想象有一个外置的
boolean flg全局变量,当我们一旦发现 左右不对称的时候,也就是我们的compare(left.left, right.right);返回值为false的时候,就将这个flg设置为false,实际上这和递归实现的效果是相同的。
那对于内侧的遍历也很好写出来了:
class Solution {public boolean isSymmetric(TreeNode root) {return compare(root.left, root.right);}public boolean compare(TreeNode left, TreeNode right) {if (left == null && right != null) {return false;}if (right == null && left != null) {return false;}if (right == null && left == null) {return true;}if (right.val != left.val) {return false;}boolean compareInside = compare(left.right, right.left);return compareInside;}
}
内侧就是首先传入根节点的 左子树,对左子树向右递归遍历,以及对右子树向左递归遍历
将这两段代码整合起来,就变成了这道题的解答
2.3 代码
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public boolean isSymmetric(TreeNode root) {return compare(root.left, root.right);}public boolean compare(TreeNode left, TreeNode right) {if (left == null && right != null) {return false;}if (right == null && left != null) {return false;}if (right == null && left == null) {return true;}if (right.val != left.val) {return false;}boolean compareOutside = compare(left.left, right.right);boolean compareInside = compare(left.right, right.left);return compareInside && compareOutside;}
}