例题:

分析:
题目要求我们必须在常数时间内检索到最小元素。
我们可以使用两个栈(A、B)来实现,A栈用来正常存储数据、弹出数据, B栈用于存储A栈中的最小元素,如下图:
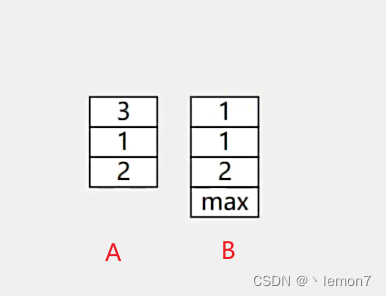
刚开始, A栈没有数据, B栈先储存一个元素MAX(整数最大值)。
添加元素时:
当向栈中加入数据时,比如先加入元素 2 , 在A栈中直接存入 2, 同时新加入元素与 B栈的栈顶元素比较,把较小值加入B栈。保证在每次加入元素后,B栈的栈顶是本次的最小元素。
弹出元素时:
当弹出元素时,A栈正常弹出元素,同时B栈也要弹出元素
代码实现:
package leetcodeup;import java.util.LinkedList;public class MinStackLeetcode155 {static class MinStack {private final LinkedList<Integer> stack = new LinkedList<>();private final LinkedList<Integer> min = new LinkedList<>();public MinStack() {min.push(Integer.MAX_VALUE);}public void push(int val) {stack.push(val);min.push(Math.min(val, min.peek()));}public void pop() {if(stack.isEmpty()){return;}stack.pop();min.pop();}public int top() {return stack.peek();}public int getMin() {return min.peek();}}
}
这是求解这道题的第一种方法。
第二种方法:
其实和第一种方法思路差不多,我们可以把新添加元素和栈里面的最小元素一起加入栈中,这样我们可以少用一个栈的空间。如下图:
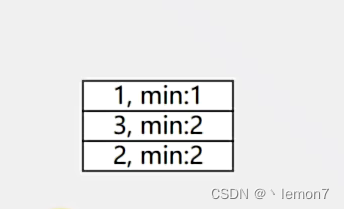
要存储这样的数据我们可以使用一种特殊的数据类型, --> record ,它是JDK16引用的新语法,
record 是一种新的关键字,用于创建不可变的(immutable)数据类,使用 record 关键字可以简化数据类的编写,并自动提供许多常见的方法,如 equals(), hashCode(), toString() 等。
record Data(int val, int min){
}
在上面的代码中,我们定义了一个名为 Data的记录类,它有两个字段 val和 min。由于这是一个 record,Java 会自动为这个类生成 equals(), hashCode(), toString(), 和一个构造函数。并为两个字段生成对应的get、set方法。
代码实现:
static class MinStack2 {record Data(int val, int min){}private final LinkedList<Data> stack = new LinkedList<>();public void push(int val) {if(stack.isEmpty()){ //第一次添加,新元素就是栈的最小值stack.push(new Data(val, val));}else{stack.push(new Data(val, Math.min(val, stack.peek().min)));}}public void pop() {stack.pop();}public int top() {return stack.peek().val;}public int getMin() {return stack.peek().min;}}


![[Git] 配置Access Token 解决Github 认证弹窗](https://img-blog.csdnimg.cn/20190712110633686.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0hvd2llWHVl,size_16,color_FFFFFF,t_70)