【蓝桥杯】线段树-编程知识

一.线段树

1.定义：

线段树是算法竞赛中常用的用来维护 区间信息 的数据结构。

线段树可以在O(logN) 的时间复杂度内实现单点修改、区间修改、区间查询（区间求和，求区间最大值，求区间最小值）等操作。

2.结构：

线段树将每个长度不为1的区间划分成左右两个区间递归求解，把整个线段划分为一个树形结构，通过合并左右两区间信息来求得该区间的信息。这种数据结构可以方便的进行大部分的区间操作。

给出一个数组A ={11,22,33,44,55},我们开始针对这个数组构造线段树。

首先将根节点编号设为1，用数组D来保存线段树，其中 $D_i$ 保存线段树上编号为i的结点的值。每个结点所维护的值就是这个节点所表示的区间总和，如下图所示：

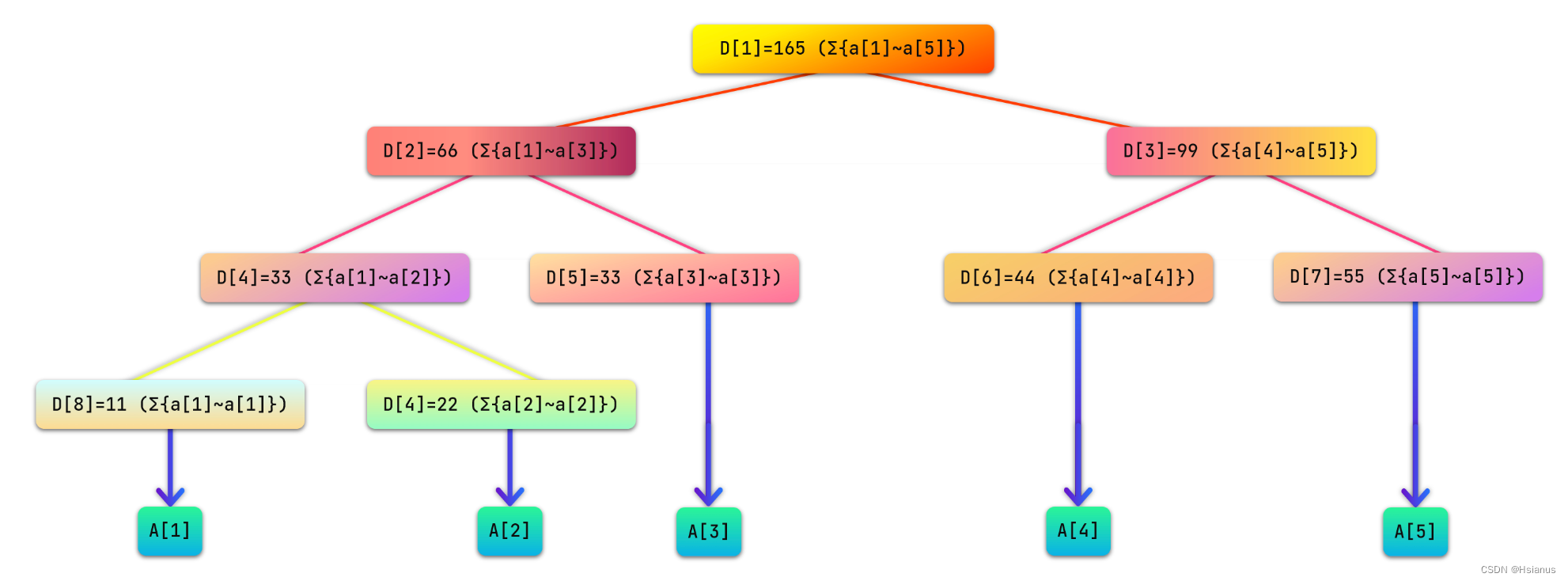
通过数据结构的知识，我们可知：i结点的左孩子的编号为2i，右孩子的编号为2i+1。

如果 $D_i$ 表示的区间为[s,t]，那么 $D_i$ 的左孩子 $D_{2i}$ 表示的区间为 $[s,\frac{s+t}{2}]$ ， $D_i$ 的右孩子 $D_{2i+1}$ 表示的区间为 $[\frac{s+t}{2}+1,t]$ 。

3.建立：

我们选择堆式存储，即用数组对线段树进行存储。

//线段树
#include <iostream>using namespace std;const int N=1e4+10;
int a[N],d[N];void merge(int x){d[x]=d[2*x]+d[2*x+1];
}void build(int x,int fisrt,int end){if(fisrt==end){d[x]=a[fisrt];return;}int mid=(fisrt+end)/2;build(2*x, fisrt, mid);build(2*x+1, mid+1, end);merge(x);
}

这里注意一点，对于一个节点来说，要么没有孩子节点，要么就有两个孩子节点。

4.区间查询：

区间查询是指：求区间[l,r]的总和，求区间最大值、最小值等操作。

int query(int x,int l,int r,int L,int R){//x表示当前查询的结点编号，[r,l]表示当前查找结点所表示的区间，[R,L]表示需要查找的区间if(l>=L&&r<=R){return d[x];}int mid=(l+r)/2;int result=0;if(L<=mid){result+=query(2*x, l, mid, L, R);}if(R>mid){result+=query(2*x+1, mid+1, r, L, R);}return result;
}

5.单点修改：

主要就是修改了一个值以后，后续的那一支的树的分支都要修改。

//单点修改
void change(int p,int l,int r,int x,int v){//将a[x]修改为v//p表示当前节点的编号，[l,r]表示当前所处的区间if(r==l){d[p]=v;return;}int mid=(l+r)/2;if(x<=mid)change(p*2, l, mid, x, v);elsechange(p*2+1, mid+1, r, x, v);merge(p);
}

6.区间修改：

在线段树中会遇到区间更新的情况，例如在区间求和问题中，令[a,b]区间内的值全部加c，若此时再采用单点更新的方法，就会耗费大量时间，这个时候就要用到懒标记(lazy标记)来进行区间更新了。

lazy标记：主要思想是，如果进行单点更新太费时间，增量就由上层暂存。lazy标记保存的是增量increment。

1）区间增加某一值

//区间更新（增加某一值）
void update(int l,int r,int c,int s,int t,int p){//[l,r]为修改区间，c为被修改区间的元素的变化量//[s,t]为当前节点所包含的区间，p为当前节点的编号if(l<=s&&t<=r){//当前区间是被修改区间的子区间d[p]+=(t-s+1)*c;//加增量lazy[p]+=c;//标记return;}int mid=(s+t)/2;if(lazy[p]!=0&&s!=t){//当前节点的lazy标记不为0，更新当前节点的两个子节点的值和lazy标记d[p*2]+=lazy[p]*(mid-s+1);lazy[p*2]+=lazy[p];d[p*2+1]+=lazy[p]*(t-mid);lazy[p*2+1]+=lazy[p];lazy[p]=0;//清空当前节点的lazy标志}if(l<=mid)update(l,r,c,s,mid,2*p);if(r>mid)update(l, r, c, mid+1, t, p*2+1);merge(p);//这里是因为有可能是包含了左/右区间的部分区间，所以要重新更新一下上层节点的值
}

2）区间查询（带lazy标志）

//区间查询
int getsum(int l,int r,int s,int t,int p){//[l,r]为查询区间，[s,t]为当前节点包含的区间，p为当前节点的编号if(l<=s&&t<=r){return d[p];}int mid=(s+t)/2;if(lazy[p]>0){//当前节点的lazy标记不为空，更新当前节点的两个子节点的值和lazy标记//此处，若是p节点没有子节点，是不可能的，因为查询到了该区间，就意味着这个区间一定是包含了待查询区间的子区间的//如果p节点没有子区间，那么s必定等于t，这个区间一定是待查询区间的子区间，在上一个if就已经返回了d[p*2]+=lazy[p]*(mid-s+1);lazy[p*2]+=lazy[p];d[p*2+1]+=lazy[p]*(t-mid);lazy[p*2+1]+=lazy[p];lazy[p]=0;//当前节点的lazy标志清空}int sum=0;if(l<=mid)sum+=getsum(l, r, s, mid, p*2);if(r>mid)sum+=getsum(l, r, mid+1, t, p*2+1);return sum;
}

3)将某一区间的值都修改为某一值

如果是修改为指定值，那么配套的区间查询函数也必须修改。

//区间修改为指定值
void fix(int l,int r,int s,int t,int p,int x){//[l,r]为查询区间，[s,t]为当前节点包含的区间，p为当前节点的编号//x为将[l,r]的区间修改为的指定值if(l<=s&&r>=t){d[p]=x*(t-s+1);lazy[p]=x;return;}int mid=(s+t)/2;if(lazy[p]>0){d[p*2]=lazy[p]*(mid-s+1);lazy[p*2]=lazy[p];d[p*2+1]=lazy[p]*(t-mid);lazy[p*2+1]=lazy[p];lazy[p]=0;//清空当前节点的lazy标志}if(l<=mid)fix(l, r, s, mid, p*2, x);if(r>mid)fix(l, r, mid+1, t, p*2+1, x);merge(p);
}
//区间查询
int get_sum(int l,int r,int s,int t,int p){if(l<=s&&r>=t){return d[p];}int mid=(s+t)/2;if(lazy[p]>0){d[p*2]=lazy[p]*(mid-s+1);lazy[p*2]=lazy[p];d[p*2+1]=lazy[p]*(t-mid);lazy[p*2+1]=lazy[p];lazy[p]=0;}int sum=0;if(l<=mid)sum+=get_sum(l, r, s, mid, p*2);if(r>mid)sum+=get_sum(l, r, mid+1, t, p*2+1);return sum;
}