一遍过。首先把区间按左端点排序,然后右端点有两种情况。
假设是a区间,b区间。。。这样排列的顺序,那么
假设a[1]>b[0],如果a[1]>b[1],就应该以b[1]为准,否则以a[1]为准。
class Solution {
public:static bool cmp(vector<int>& a ,vector<int>& b){return a[0]<b[0];}int eraseOverlapIntervals(vector<vector<int>>& intervals) {if(intervals.size()==0) return 0;sort(intervals.begin(),intervals.end(),cmp);int res=0;for(int i=1;i<intervals.size();i++){if(intervals[i][0]<intervals[i-1][1]){res++;intervals[i][1]=min(intervals[i][1],intervals[i-1][1]);}}return res;}
};题解方法:
我来按照右边界排序,从左向右记录非交叉区间的个数。最后用区间总数减去非交叉区间的个数就是需要移除的区间个数了
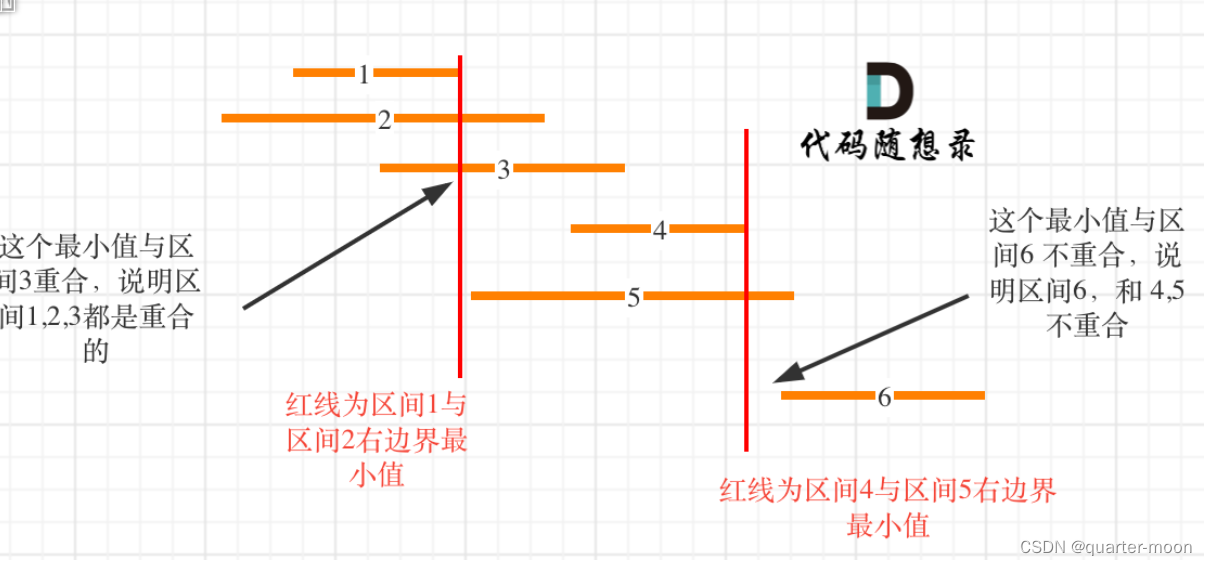
就是取 区间1 和 区间2 右边界的最小值,因为这个最小值之前的部分一定是 区间1 和区间2 的重合部分,如果这个最小值也触达到区间3,那么说明 区间 1,2,3都是重合的。
接下来就是找大于区间1结束位置的区间,是从区间4开始。那有同学问了为什么不从区间5开始?别忘了已经是按照右边界排序的了。
区间4结束之后,再找到区间6,所以一共记录非交叉区间的个数是三个。
总共区间个数为6,减去非交叉区间的个数3。移除区间的最小数量就是3。
class Solution {
public:// 按照区间右边界排序static bool cmp (const vector<int>& a, const vector<int>& b) {return a[1] < b[1];}int eraseOverlapIntervals(vector<vector<int>>& intervals) {if (intervals.size() == 0) return 0;sort(intervals.begin(), intervals.end(), cmp);int count = 1; // 记录非交叉区间的个数int end = intervals[0][1]; // 记录区间分割点for (int i = 1; i < intervals.size(); i++) {if (end <= intervals[i][0]) {end = intervals[i][1];count++;}}return intervals.size() - count;}
}; 
看了题解。
在遍历的过程中相当于是要找每一个字母的边界,如果找到之前遍历过的所有字母的最远边界,说明这个边界就是分割点了。此时前面出现过所有字母,最远也就到这个边界了。
可以分为如下两步:
- 统计每一个字符最后出现的位置
- 从头遍历字符,并更新字符的最远出现下标,如果找到字符最远出现位置下标和当前下标相等了,则找到了分割点
class Solution {
public:vector<int> partitionLabels(string s) {int hash[27]={0};for(int i=0;i<s.size();i++){hash[s[i]-'a']=i;}vector<int> res;int left=0;int right=0;for(int i=0;i<s.size();i++){right=max(right,hash[s[i]-'a']);if(right==i){res.push_back(right-left+1);left=i+1;}// else{// }}return res;}
}; 
一遍过。将区间按左端点从小到大排序。假设是排序后是a,b,。。。
假设b区间左端点b[0]小于等于a区间右端点a[1],有两种情况:1、a[1]<b[1],那么合并区间选择b[1]。2、a[1]>b[1],就选a[1],而合并区间左端点始终选择a[0];
假设b[0]>a[1],那么就可以把上次融合后的区间加入结果。
class Solution {
public:
static bool cmp(const vector<int>& a,const vector<int>& b){return a[0]<b[0];
}vector<vector<int>> merge(vector<vector<int>>& intervals) {vector<vector<int>> res;sort(intervals.begin(),intervals.end(),cmp);for(int i=1;i<intervals.size();i++){if(intervals[i][0]<=intervals[i-1][1]){intervals[i][1]=max(intervals[i][1],intervals[i-1][1]);intervals[i][0]=intervals[i-1][0];}else{res.push_back(intervals[i-1]);}}res.push_back(intervals[intervals.size()-1]);return res;}
};题解写法:
class Solution {
public:vector<vector<int>> merge(vector<vector<int>>& intervals) {vector<vector<int>> result;if (intervals.size() == 0) return result; // 区间集合为空直接返回// 排序的参数使用了lambda表达式sort(intervals.begin(), intervals.end(), [](const vector<int>& a, const vector<int>& b){return a[0] < b[0];});// 第一个区间就可以放进结果集里,后面如果重叠,在result上直接合并result.push_back(intervals[0]); for (int i = 1; i < intervals.size(); i++) {if (result.back()[1] >= intervals[i][0]) { // 发现重叠区间// 合并区间,只更新右边界就好,因为result.back()的左边界一定是最小值,因为我们按照左边界排序的result.back()[1] = max(result.back()[1], intervals[i][1]); } else {result.push_back(intervals[i]); // 区间不重叠 }}return result;}
};