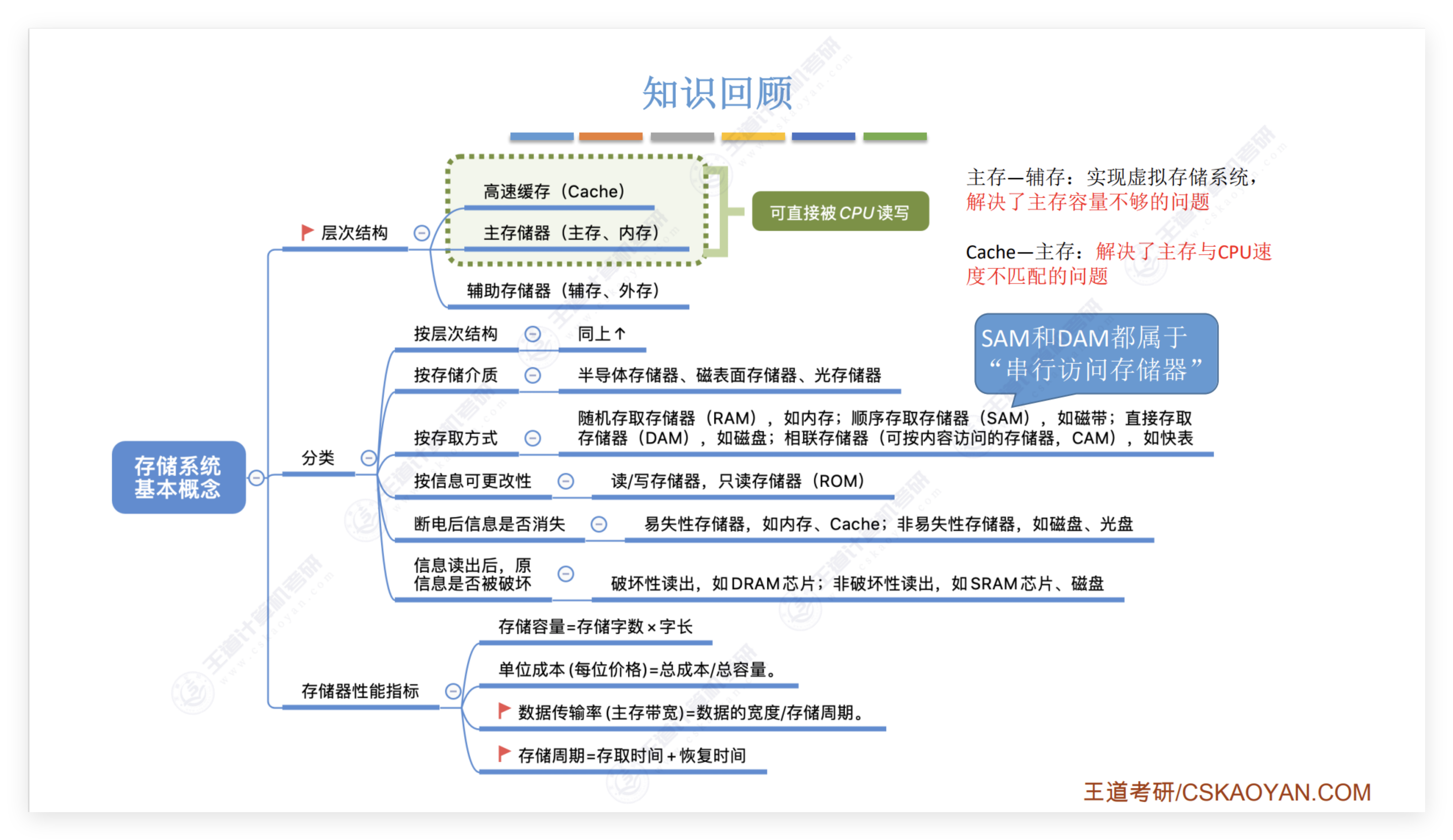
原题链接
题解
假如不是环,你会做吗?
从左到右遍历 \(i\) 第 \(i\) 棵树的放置只与前面一棵树有关,线性dp
而图一定长这样:
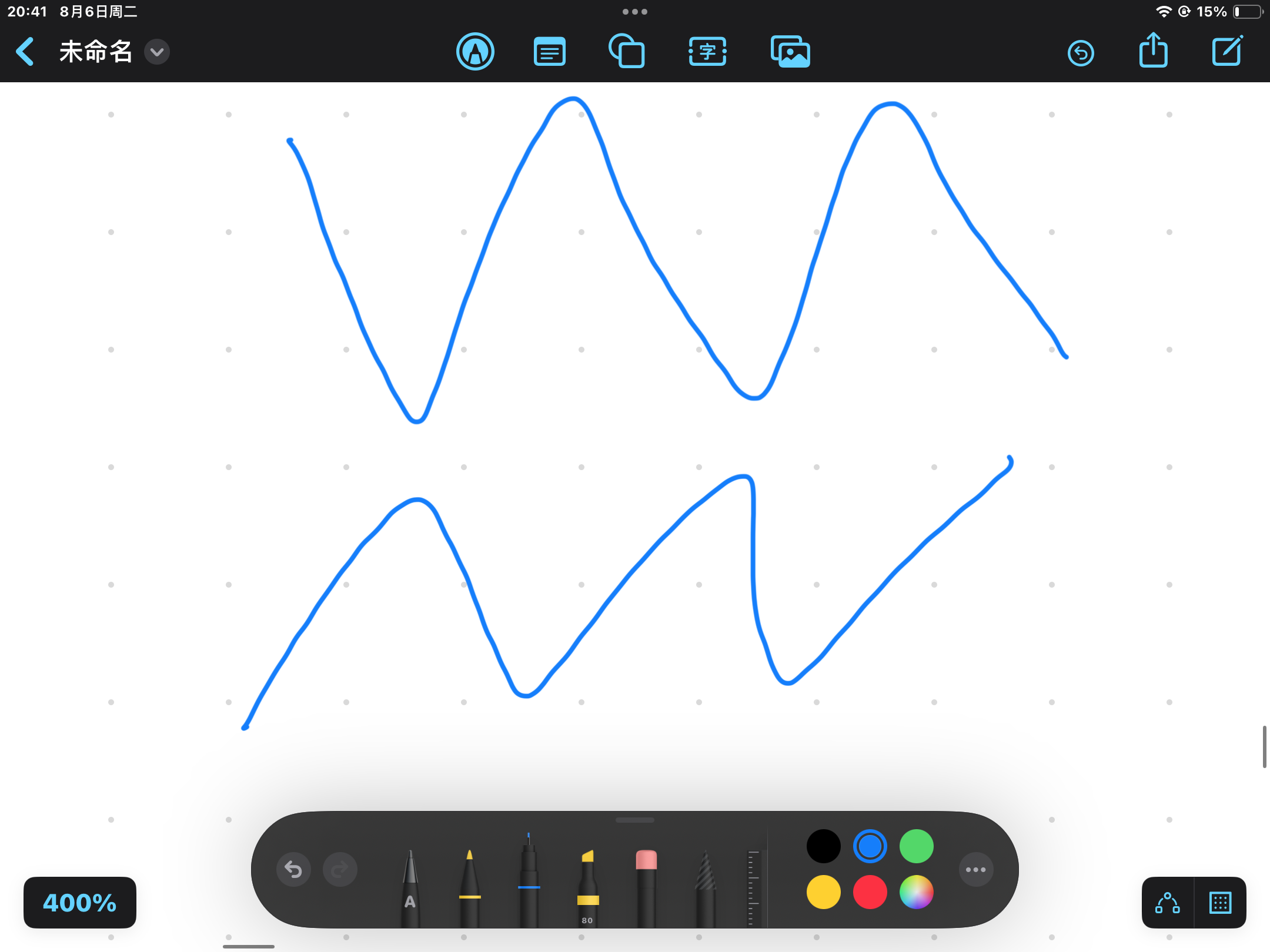
当第 \(n\) 棵树为 \(3\) 的时候,无论第一棵树是 \(1\) 还是 \(2\)(不能为3,因为3不会往上),都符合环的要求
\(1\) 同理
因此我们只需要考虑第 \(n\) 棵树为 \(2\) 的情况
假如第 \(n\) 棵树是 \(2\),那么第 \(1\) 棵树不是1就是3,因此只需要把第一棵树移到 \(n+1\) 的位置再进行一次dp即可
code
#include<bits/stdc++.h>
using namespace std;
/*
#define int long long
#define double long double
#define lowbit(x) ((x)&(-x))
const ll inf=1e18;
const ll mod=1e9+7;const ll N=4e5;
ll qpow(ll a,ll n)
{ll res=1;while(n){if(n&1) res=res*a%mod;a=a*a%mod;n>>=1;}return res;
}
ll inv(ll x)
{return qpow(x,mod-2);
}
ll fa[2000005];
ll finds(ll now){return now==fa[now]?now:finds(fa[now]);}vector<ll> G[200005];ll dfn[200005],low[200005];
ll cnt=0,num=0;
ll in_st[200005]={0};
stack<ll> st;
ll belong[200005]={0};void scc(ll now,ll fa)
{dfn[now]=++cnt;low[now]=dfn[now];in_st[now]=1;st.push(now);for(auto next:G[now]){if(next==fa) continue;if(!dfn[next]){scc(next,now);low[now]=min(low[now],low[next]);}else if(in_st[next]){low[now]=min(low[now],dfn[next]);}}if(low[now]==dfn[now]){ll x;num++;do{x=st.top();st.pop();in_st[x]=0;belong[x]=num;}while(x!=now);}
}
vector<int> prime;
bool mark[200005]={0};
void shai()
{for(int i=2;i<=200000;++){if(!mark[i]) prime.push_back(i);for(auto it:prime){if(it*i>200000) break;mark[it*i]=1;if(it%i==0) break;}}
}
*/int a[100005][5];int dp[100005][5][5]={0};void solve()
{int n;cin>>n;for(int i=1;i<=n;i++) cin>>a[i][1]>>a[i][2]>>a[i][3];for(int i=1;i<=n;i++){dp[i][1][1]=dp[i-1][2][2]+a[i][1];dp[i][1][1]=max(dp[i][1][1],dp[i-1][3][2]+a[i][1]);dp[i][2][1]=dp[i-1][3][2]+a[i][2];dp[i][2][2]=dp[i-1][1][1]+a[i][2];dp[i][3][2]=dp[i-1][2][1]+a[i][3];dp[i][3][2]=max(dp[i][3][2],dp[i-1][1][1]+a[i][3]);}int ans=0;ans=max(ans,dp[n][1][1]);ans=max(ans,dp[n][3][2]);memset(dp,0,sizeof dp);for(int i=1;i<=3;i++) a[n+1][i]=a[1][i];for(int i=2;i<=n+1;i++){dp[i][1][1]=dp[i-1][2][2]+a[i][1];dp[i][1][1]=max(dp[i][1][1],dp[i-1][3][2]+a[i][1]);dp[i][2][1]=dp[i-1][3][2]+a[i][2];dp[i][2][2]=dp[i-1][1][1]+a[i][2];dp[i][3][2]=dp[i-1][2][1]+a[i][3];dp[i][3][2]=max(dp[i][3][2],dp[i-1][1][1]+a[i][3]);}ans=max(ans,dp[n+1][1][1]);ans=max(ans,dp[n+1][3][2]);cout<<ans<<'\n';
}
signed main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int TT=1;//cin>>TT;while(TT--) solve();return 0;
}