Lecture 05 Real-time Environment Mapping
Recap: Environment Lighting
- 一张表示了来自四面八方的无穷远处光(distance lighting)的图片
- Spherical map vs. cube map
Shading from environment lighing
非正式地命名为Image-Based Lighting (IBL)
- 通用解法:Monte Carlo intergration蒙特卡洛积分
- 数值上无偏的近似
- 需要大量的样本
- 问题:非常慢
- 通常,如果shader中出现了sampling,很可能就不能用在实时渲染中
- 因为tempore的进展,时间、空间的滤波方式,sample复用的方式,使得越来越多的基于sampling的方法可以在实时渲染中应用了
- 但是还是尽量避免sampling
- 尽可能避免sampling
- 通常,如果shader中出现了sampling,很可能就不能用在实时渲染中
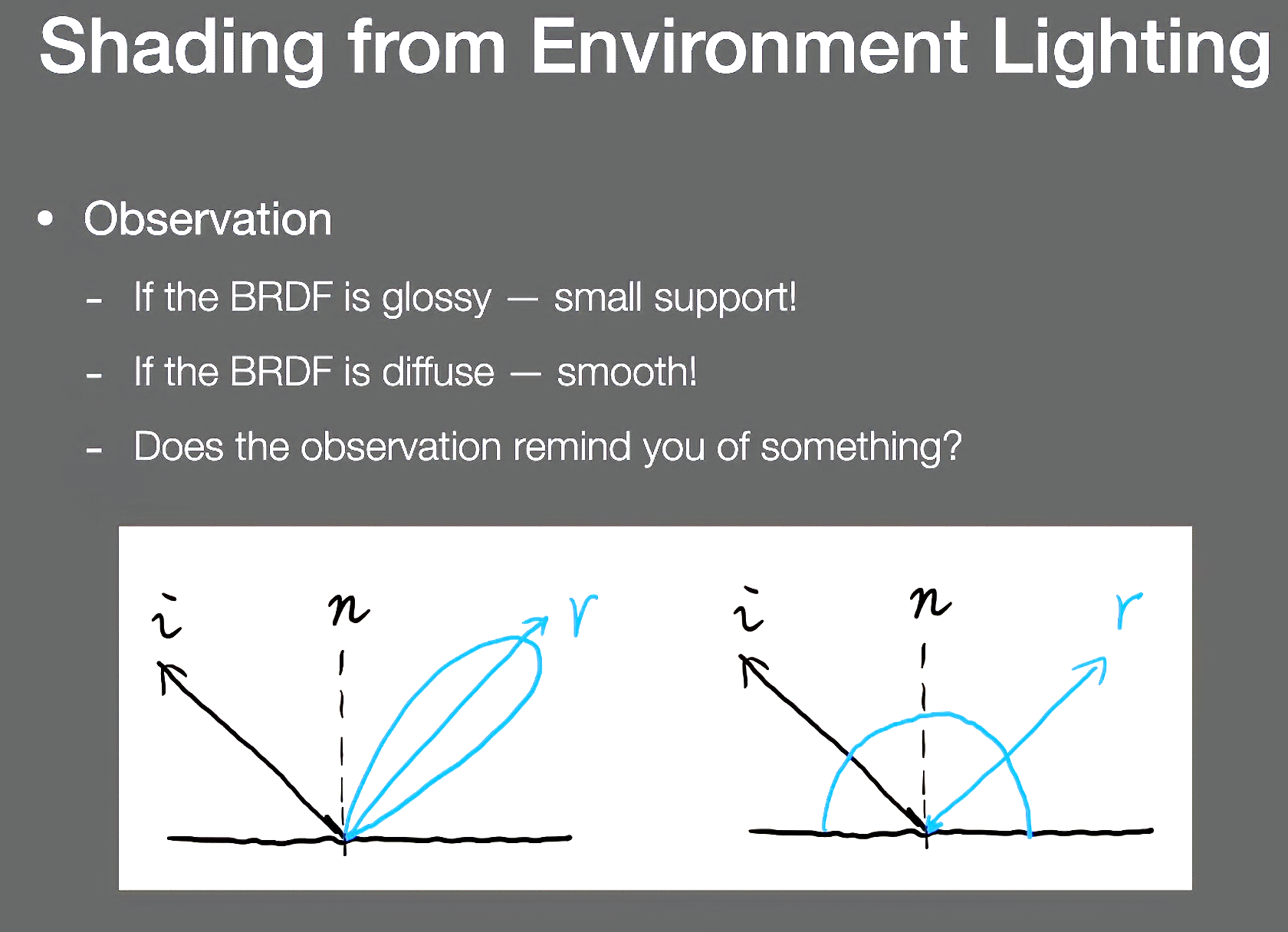
渲染方程Lighting项和BRDF项相乘再积分
- 如果BRDF项是glossy的(左图),说明覆盖球面的情况下覆盖的挺小(support小)
- 如果BRDF项是diffuse的(右图),覆盖半球区域大,但是非常smooth
于是可以用经典的近似方案:
条件:
- g(x)的support比较小
- g(x)比较smooth
满足其一即可
将Lighting项拆出来,表示为光照在BRDF项范围的积分,再除以一个在BRDF项范围内的空积分来做归一化
*区别于前面Shadow Map,Shadow Map中是将Visibility项拆出来,这里是将Light拆出来
也可以理解成拆出来的项是在滤波,而support的大小决定了filter核的大小
The split sum approximation
1st Stage Prefiltering
这里是在球面上做预计算
- 用不同大小的滤波核近似
- 查询时通过上一步生成的图中三线性插值得到中间filter size的图(类似Mipmap)
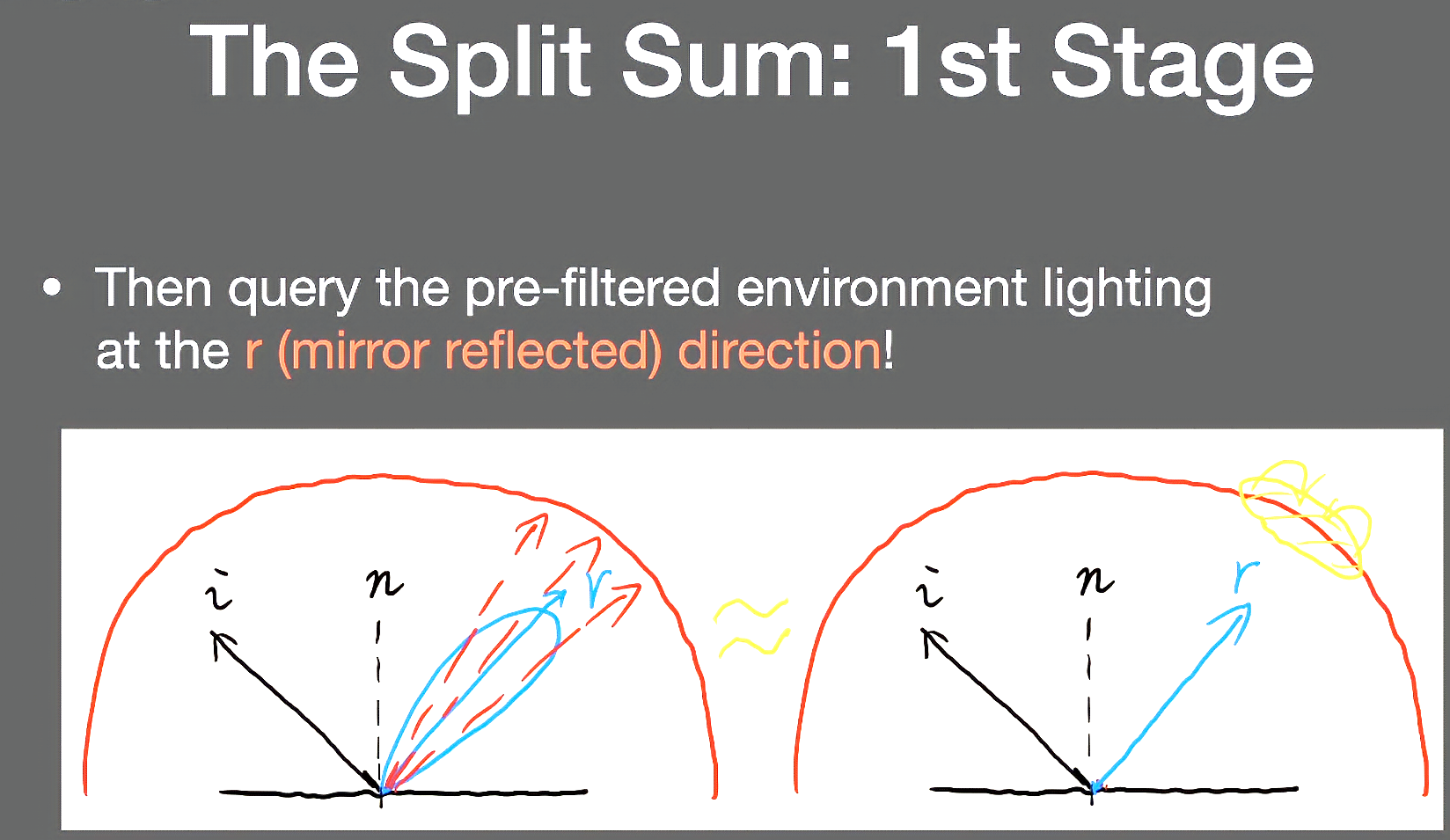
为什么要做filtering?
要计算一个shading point对应的环境光项,会在其周围分布一些采样,再做加权平均,从而得到shading point的值
这个操作就约等于先对环境光做好一个filtering,这样采样到的环境光的任何一个点都是原先一系列点的加权平均,于是就只需在镜面反射的方向上查询一次
这里对应的是前面渲染方程中拆出来的Lighting项
2nd Stage
思想:
- 预计算所有可能的参数(roughness, color (Fresnel term) )的不同组合得出的值
- 这样做参数太多,需要一个五维的表来记录结果(roughness一维,rgb三维,角度一维)
- 预计算是非常正常的做法,但可能无法承受高纬度的预计算
- 如何降低维度?
Recall: Microfacet BRDF 微表面BRDF
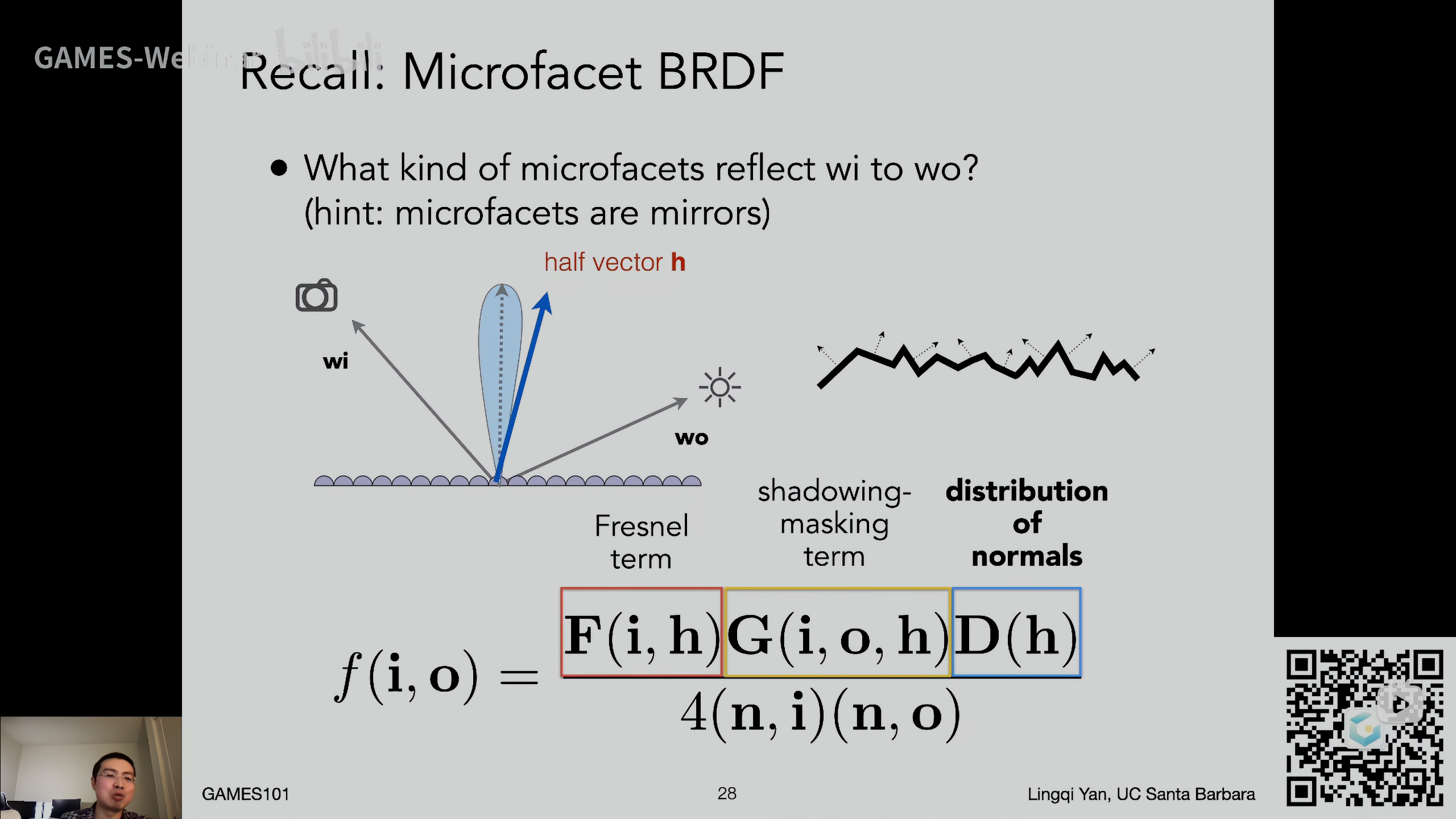
Schlick's approximation
能够近似地描述菲涅尔项,将其近似成一个指数函数,定义了一个初始反射率\(R_0\),以及函数如何增长\((1-\cos\theta)^5\)
Beckmann distribution
NDF项使用Beckmann distribution,结果只与粗糙度\(\alpha\)和半程向量与法线夹角\(\theta_h\)有关
降维后的预计算
于是就将刚刚五维的预计算变成了三维的预计算,参数为\(初始反射率R_0,入射角\theta,roughness\ \alpha\)
继续降维:
将\(R_0\)拆到了积分外边,将原本积分对于基础反射率\(R_0\)的依赖给消除了,BRDF中的\(f_r\)和菲涅尔项\(F\)上下消掉了,剩下的只有两个参数\(\theta_i和\alpha\),降到了二维,这样两个积分部分刚好放在一张纹理的两个通道,于是计算环境光照只需求查询纹理,不需要采样了
- 计算避免了sampling
- 非常快且结果正确
在工业界叫做split sum
- split integral 积分\(\rightarrow\)split sum 求和
- \(\frac{1}{N}\underset{k=1}{\overset{N}\sum}\frac{L_i(l_k)f(l_k,v)\cos\theta_{l_k}}{p(l_k,v)}\approx(\frac{1}{N}\underset{k=1}{\overset{N}{\sum}}L_i(l_k))(\frac{1}{N}\underset{k=1}{\overset{N}{\sum}}\frac{f(l_k,v)\cos\theta_{l_k}}{p(l_k,v)})\)
![[转]高斯-牛顿算法](https://img-blog.csdn.net/20160609002742523)


![[转]OpenCV4.8 GPU版本CMake编译详细步骤 与CUDA代码演示](https://img2024.cnblogs.com/blog/494924/202409/494924-20240901123955342-1942084893.png)
![[图文直播]搭建Zfile私有网盘](https://img2023.cnblogs.com/blog/3485711/202409/3485711-20240901122652658-1117766162.png)