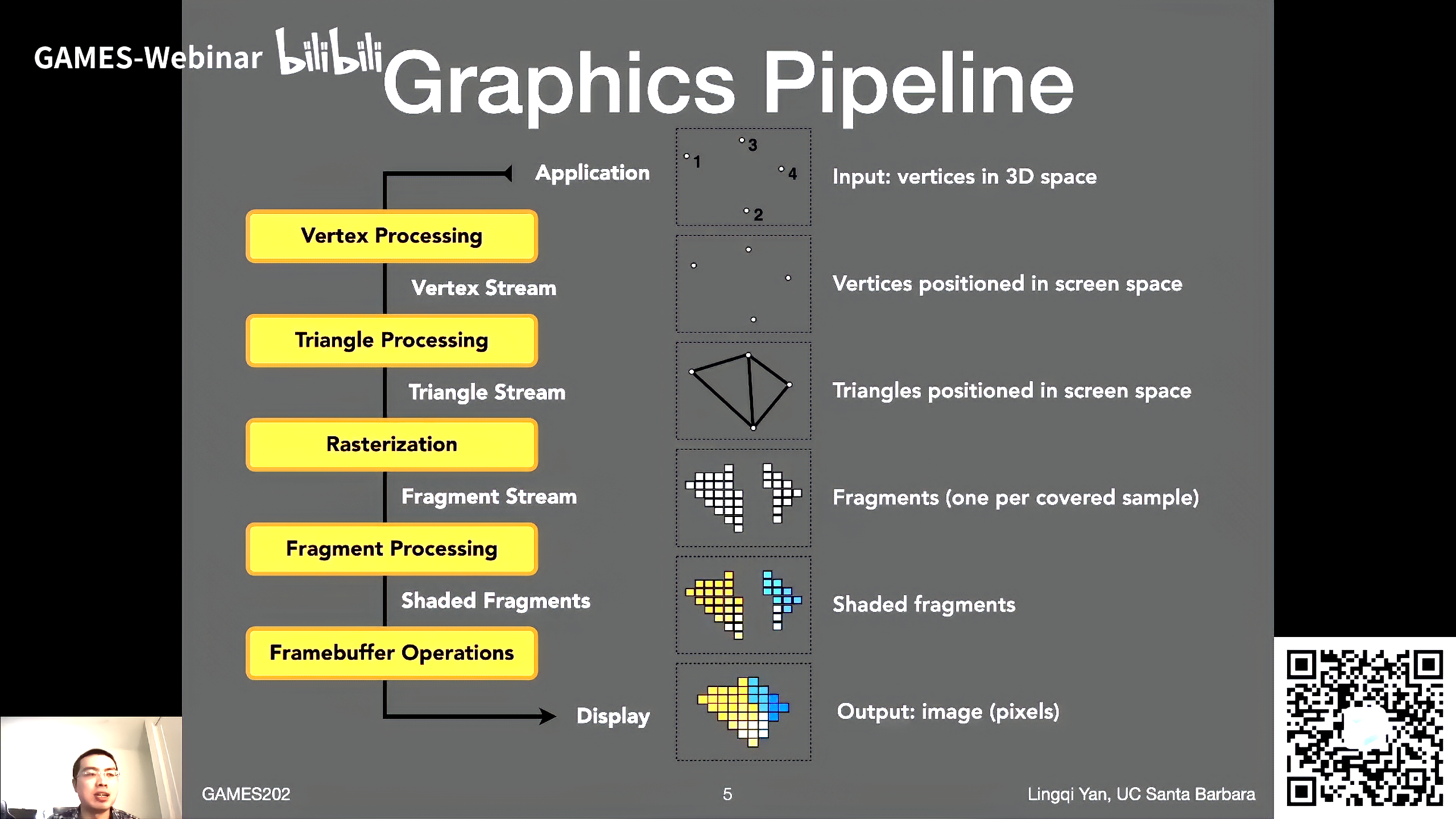
Lecture 04 Real-time Shadows 2
PCF and PCSS
PCF背后的数学知识
Filter / convolution:
如果对某个函数\(f\)做卷积,可以用\([\omega * f](p)=\underset{q \in \Nu (p)}{\sum}w(p,q)f(q)\)
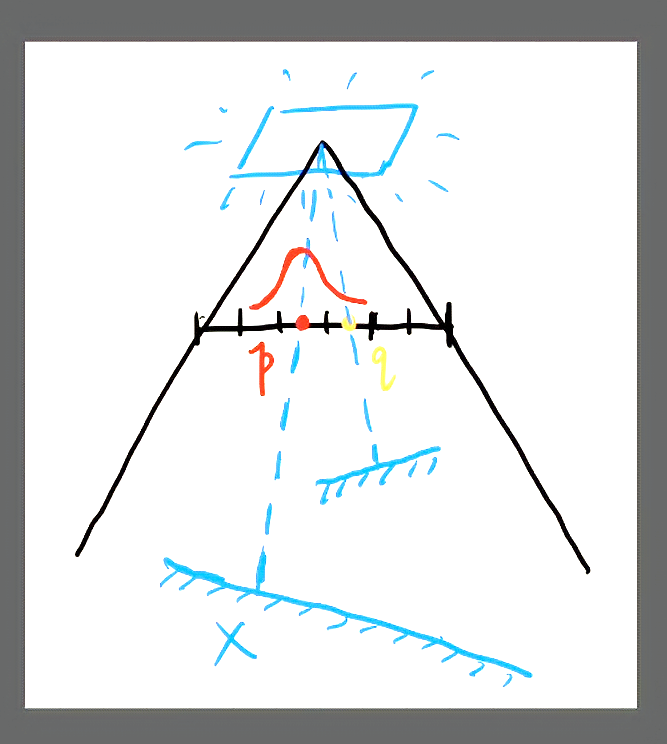
比如PCSS中对某一点q周围区域做卷积求visibility
\(V(x)=\underset{q\in \Nu(p)}{\sum}w(p,q)\cdot \chi^+[D_{SM}(q)-D_{Scene}(x)]\)
\(\chi^+是一个符号函数,变量大于0为1,否则结果为0,对应了阴影比较结果(公式中SM指shadow map)\)
性能分析
PCSS算法:
- step 1: Blocker search
- step 2: Penumbra estimation
- step 3: Percentage Closer Filtering
step1和step3导致慢
优化方案:
-
step1和step3只对某些texel采样(近似),这样会导致visiblity图存在noise,可以对这张visibility图进行图像空间上的降噪(降噪方面详细见Real-time Raytracing)
噪声会导致flicker,flicker就是每一帧取的随机数不一样,每一帧的noise也不一样,每一帧都是noisy的,且播放速度很快,就会导致画面非常抖
-
Variance soft shadow mapping (VSSM / VSM)
Variance soft shadow mapping (VSSM/VSM)
可以理解为PCSS的快速版本
Step 3
PCSS的思想是取shading point对应点周围的深度,看有多少深度在阴影里,并平均(不加权的情况下)
在VSSM中,为了做第三步的PCF,想要知道自己在周围的深度中排百分之几,只要能拿到这个区域内的平均深度和方差,就能用正态分布近似了
- Mean (average) 平均值
- 使用MIPMAP,但是MIPMAP不准确,且只能是正方形的
- Summed Area Tables (SAT),一个更精准的数据结构
- Variance 方差
- \(Var(X)=E(X^2)-E^2(X)\),概率论中的公式,方差等于平方的均值减均值的平方
- 于是需要额外一张Shadow Map记录每个pixel深度的平方
- 一个texel中有RGBA四个通道,而depth只需一个通道,只要生成Shadow Map时,顺便将\(depth^2\)写在别的通道,根本就不需要额外一张Texture

有了正态分布PDF(概率分布函数),于是知道了有多少texel要比shading point对应点的深度小,有多少更大(百分比),只需统计面积即可
如果把有多少深度小于自己做成一张图,就是CDF 累计分布函数(右图)
如何求CDF?将积分的值打表,积分出的值叫\(error\ function\ 误差函数\)。积分没有解析解,只有数值解,C++中可用erf函数求解,于是就省去打表了
Chebychev 切比雪夫不等式
\(P(x>t) \le \frac{\sigma^2}{\sigma^2+(t-\mu)^2}\)
\(\mu为均值,\sigma为方差\)
如果有一个正态分布,知道均值,知道方差,就能定义出一个正态分布函数,给出自变量\(t\),就能知道大于 \(t\)的概率有多少
-
切比雪夫不等式不需要知道这个分布是不是正态分布,它会认为这个一个比较简单的单峰分布,求得对应分布不会超过给出的结果,而在实时渲染中,一般不考虑不等,只考虑约等,所以直接当等于用了
-
但是切比雪夫不等式有一个苛刻的条件,那就是要查询的\(t\)必须在均值\(\mu\)的右边
因为我们要查询的是这个点被遮挡的概率(百分比),几乎就确定了它是被遮挡了一部分,因此它的深度往往比周围点的深度大
总结
- Perfomance
- 生成Shadow Map,同时生成平方深度map(写在Shadow Map另一个通道即可)
- 其他(让Shadow Map和平方Shadow Map能够支持范围查询的工作)
- Run time
- 查询均值:\(O(1)\)
- 查询方差:\(O(1)\)
- Chebychev : \(O(1)\)
- 完全不需要采样或者循环
- 完美解决step 3(?)
Step 1
-
Block search
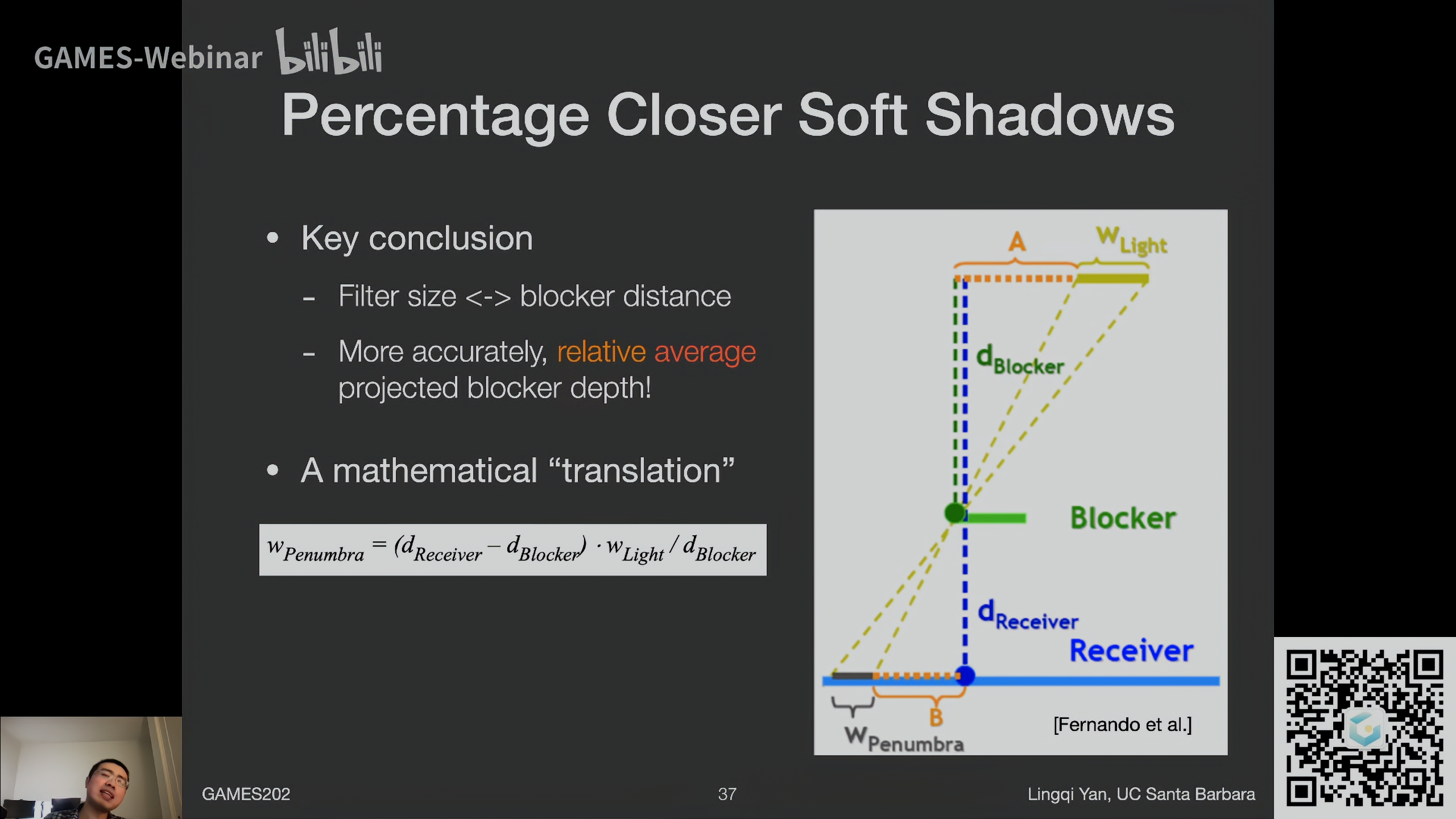
Key idea
-
Blocker(\(z<t\) ), \(avg.Z_{occ}\)(想要求的东西)
-
Non-blocker(\(z>t\)), \(avg.Z_{unocc}\) (未知)
-
\(\frac{N_1}{N}z_{unocc}+\frac{N_2}{N}z_{occ}=z_{Avg}\)
-
近似:\(N_1/N=P(x>t),\ Chebychev\)
-
近似:\(N_2/N = 1-P(x>t)\)
-
继续近似:认为非遮挡物的深度与shading point一样 \(z_{unocc}=t\) (i.e. shadow receiver is a plane)
绝大多数阴影接收者是个平面
-
PCSS 对比 VSSM
VSSM不存在任何噪声,因为噪声只会由于采样数不足而产生,虽然VSSM做了很多假设,但没有进行部分采样
VSSM没有使用正态分布进行估计,使用的是切比雪夫
现在更多使用PCSS(部分采样),因为现在在图像空间降噪的手段越来越强, 于是对噪声的容忍度越来越高
MIPMAP and Summed-Area Variance Shadow Maps
对于均值\(\mu\),是一个矩形的范围查询
MIPMAP
快速、近似、方向的范围查询
但是不准,因为是通过线性插值生成的
SAT
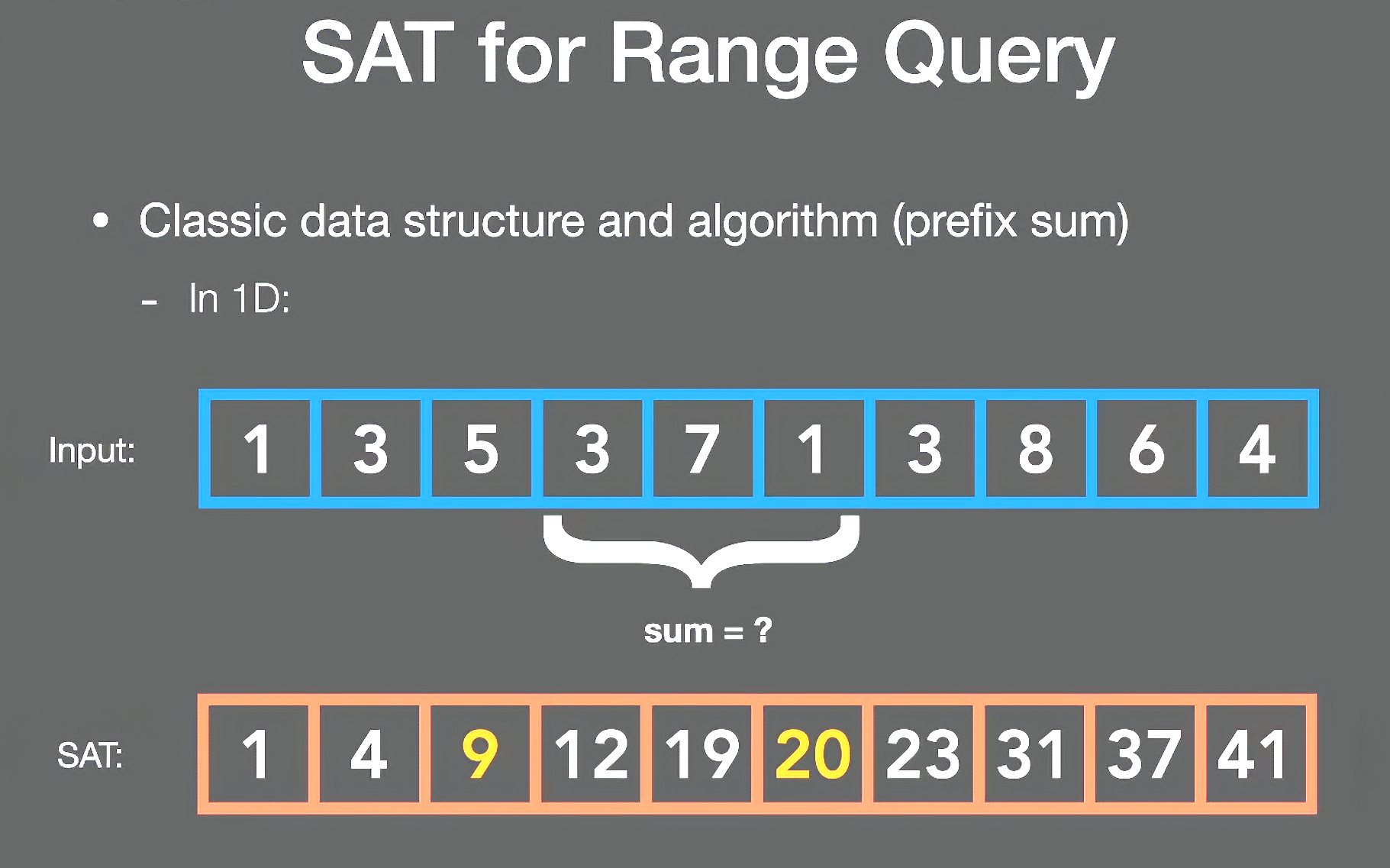
范围内求和和范围内求平均是等价的,类似前缀和,上图为一维情况
中间任意一段可以表示为当前这段减去前面一段
如:4~6的平均等于前6项的和减前3项的和
二维情况:
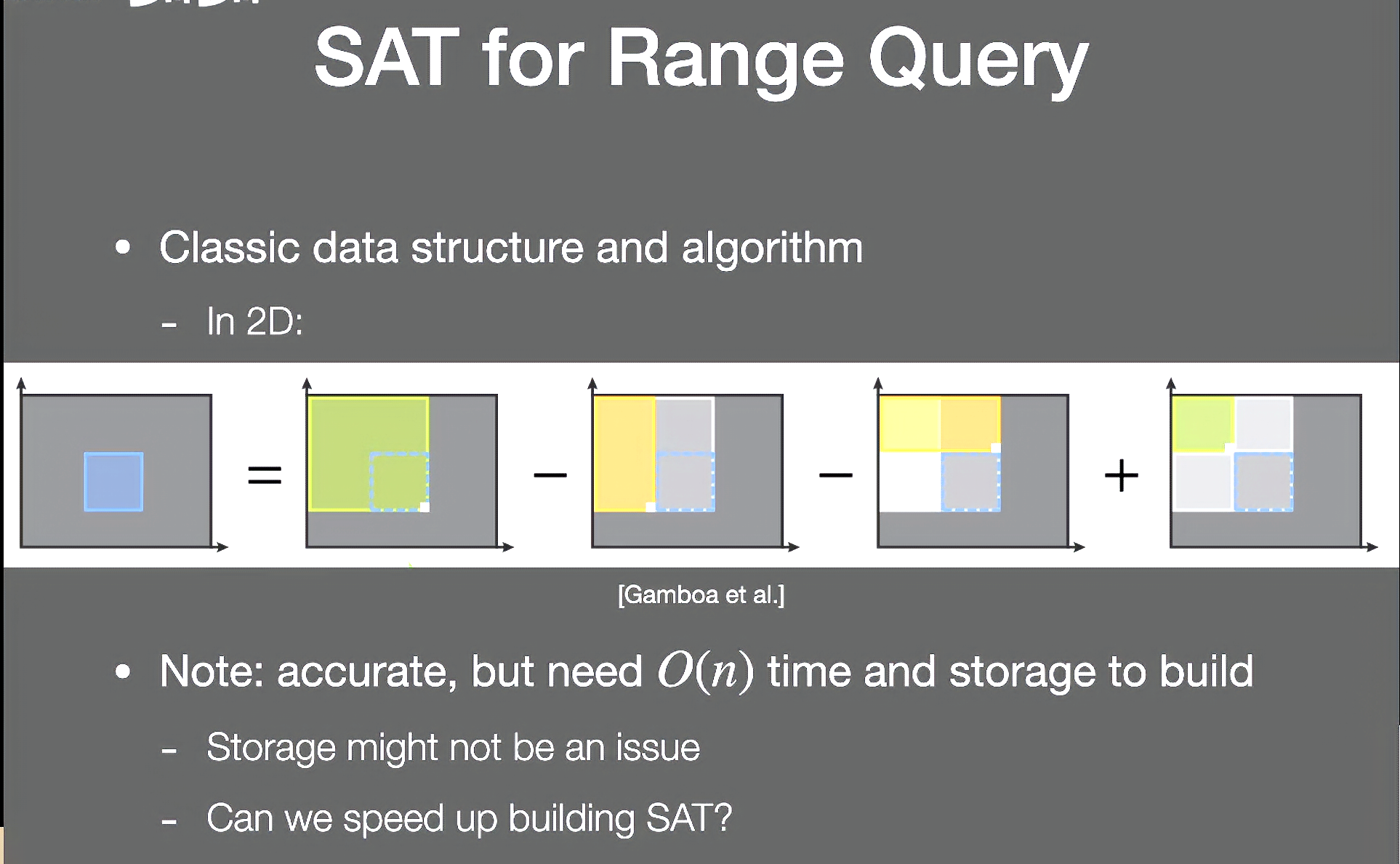
容斥原理
要求蓝色矩形的均值,只需用大绿色矩形减去两个黄色矩形,再补上小的绿色矩形
矩形起点都是左上角,于是可以预计算一张SAT(每行都是一个一位数组,每一列同理)
Moment shadow mapping
VSSM的问题

对于不能认为范围内texel的深度是光滑的单峰分布时,如右图范围内,有三个窗口,应有三个峰值,所以不能用高斯分布来描述
得到结果要么大要么小
- Overly dark: may be acceptable
- Overly bright: LIGHT LEAKING 人们不希望某些阴影的地方突然变白了
另一个问题:Chebychev不等式只有当\(t>z_{avg}\)时才准确
MSM
- 目标:解决VSSM分布描述不准确的问题
- 思想:使用更高阶的moments(矩)来描述分布
Moment
-
最简单的解释:几阶的矩就是一个数的几次方
-
所以VSSM使用了一阶和二阶的矩
-
使用更高阶的矩,分布就更准确
使用\(m\)阶的矩,就能表示有\(m/2\)个step(台阶)的函数
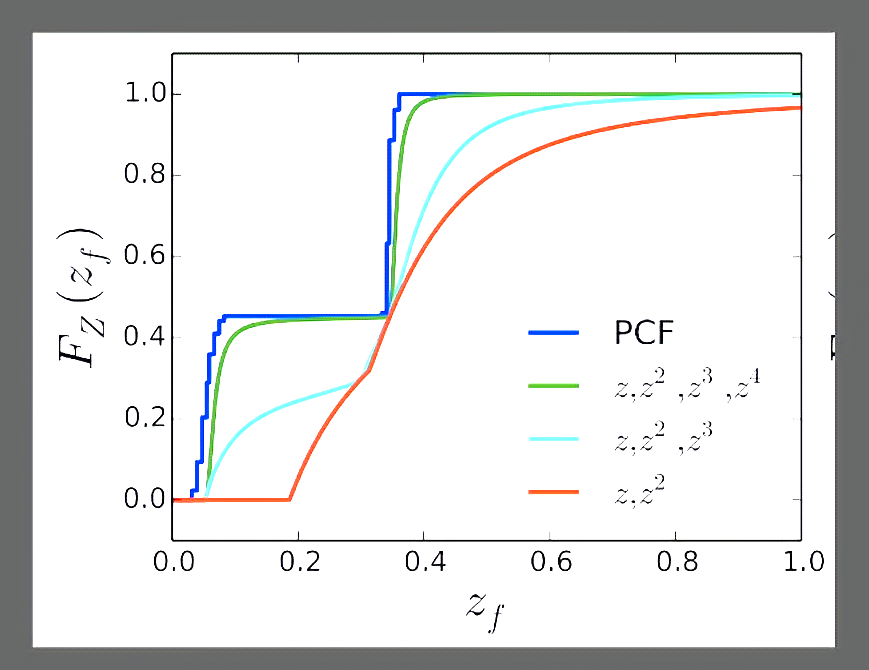
比如绿色的函数,使用了4阶矩,所以有2个台阶,且已经和PCF接近
4阶刚好对应RGBA四通道,且阶高了精度不好
工业界数过多,且不考虑精度时的做法,packing and unpacking
将float32的数用float16表示,两个float16的数放在一个float32里,可以省一半的存储空间,但是这样就不能插值了(或者得unpack后手动插值)
MSM的问题
-
存储(问题不是太大)
-
性能消耗(已经前几阶的矩,如何恢复出函数)
详见[Peters et al., Moment Shadow Mapping]
-
Distance field soft shadows
Distance function
在空间中任意一点,给出这个点到物体表面的最短距离(可以是带符号的),带符号的称为Sighed distance field (SDF)
SDF可以做任意形状物体的blend,得到几何上非常好的一个过渡,而不需要考虑物体的形状
但是SDF生成的物体表面非常不好贴纹理,参数化不好得到
The Usage of Distance Field
Ray marching
- Ray marching (sphere tracing) to perform ray-SDF intersection
- SDF定义了到物体表面的最短距离,因此在这个距离以内不存在任何物体
- 因此一束光线出发前用SDF得出到任意物体表面的最短距离后,可以直接移动这个距离,这样一定不会发生任何相交,只会再重复这个过程
- 因此,任何时刻在\(p\)点,移动\(SDF(p)\)的距离
Soft shadow

- 使用SDF近似地定义被遮挡的百分比
- SDF的值表示了一个安全角度
- 安全角度越小,表示被遮挡的越多,阴影越黑
- 把安全角度简单转换成了阴影值
*SDF不能得知遮挡物的方位
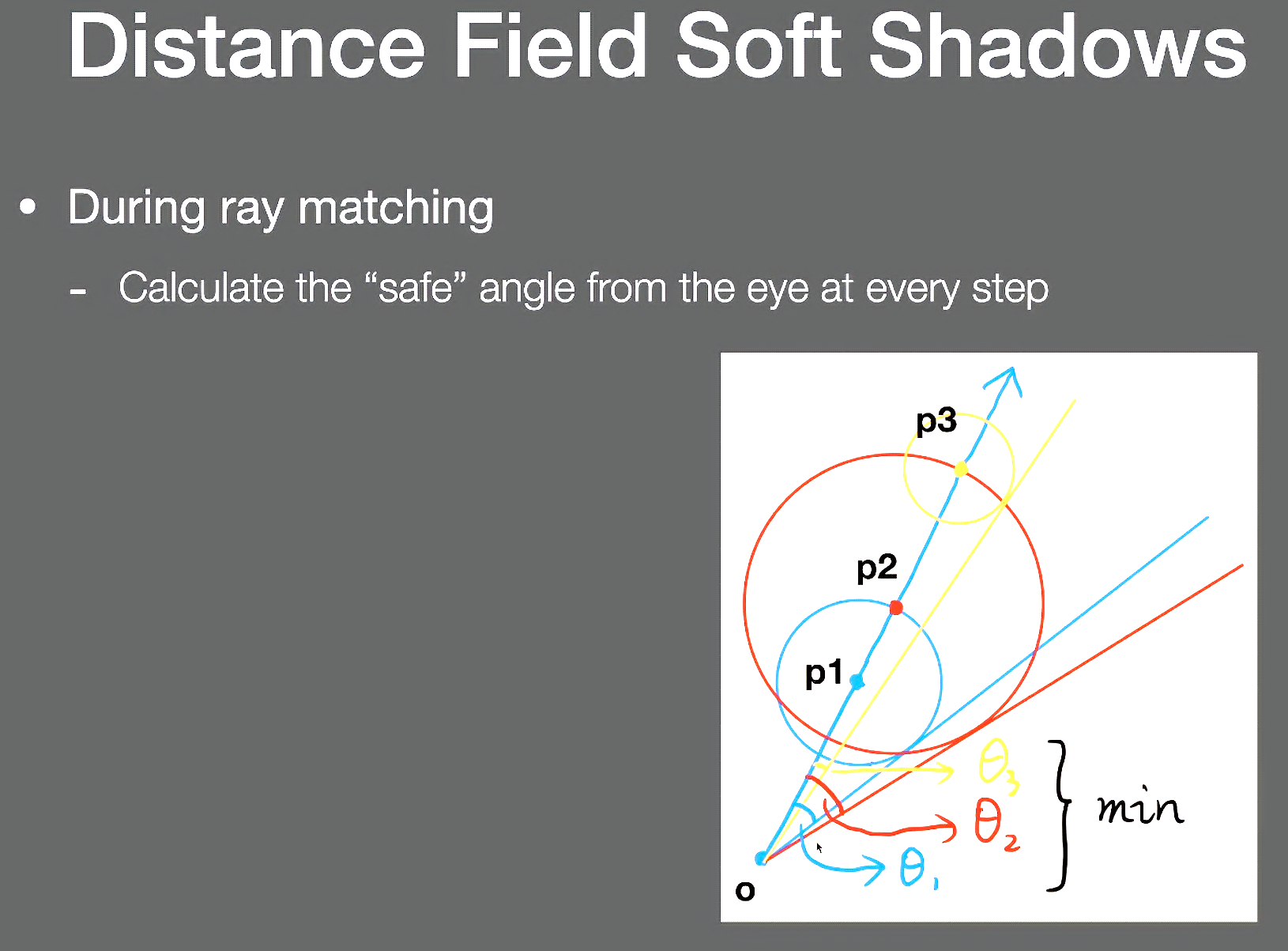
-
每一个step都能得到一个安全角度
-
最终的安全角度就是所有安全角度的最小值
-
SDF得到值是直角边,ray移动的距离是斜边,只需计算一个\(\arcsin\)即可
\(arcsin\frac{SDF(p)}{p-o}\) ?
\(min\{\frac{k\cdot SDF(p)}{p-o}, 1.0\}\)
算\(\arcsin\)复杂, 直接用比值近似,转化成visibility,不能超过1
- k为1时什么也没做
- k比较大时,很小的安全角度也会被当成1,0~1的过渡带就会小,k极大时相当于硬阴影
- 所有k用来控制阴影的软硬程度
SDF得到的阴影相较PCSS和VSSM更加虚假
Pros and Cons of Distance Field
- Pros 优点
- 快*(仅考虑使用SDF而没有考虑生成SDF)
- High quality
- Cons 缺点
- 需要预计算
- 需求非常大存储空间
- Artifact?
Antiliased / infinite resolution characters in RTR
- Unity 的TextMeshPro
![[转]高斯-牛顿算法](https://img-blog.csdn.net/20160609002742523)


![[转]OpenCV4.8 GPU版本CMake编译详细步骤 与CUDA代码演示](https://img2024.cnblogs.com/blog/494924/202409/494924-20240901123955342-1942084893.png)
![[图文直播]搭建Zfile私有网盘](https://img2023.cnblogs.com/blog/3485711/202409/3485711-20240901122652658-1117766162.png)