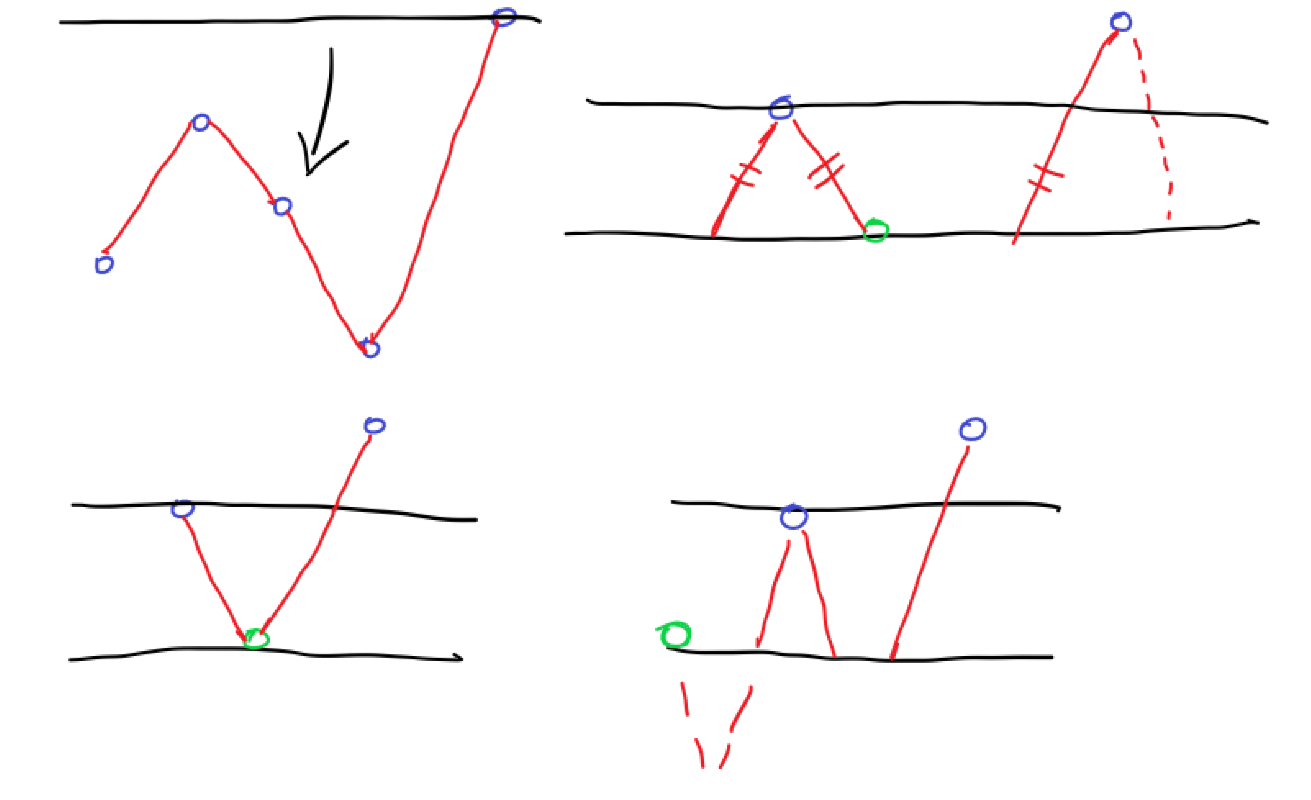
平面内到定点 \(F(c,0)\)的距离和到定直线 :\(\displaystyle l:x=\frac{a^{2}}{c}\)( 点\(F\)不在\(l\)上)的距离之比为常数\(\displaystyle \frac{a}{c}\)(即离心率\(e\),\(0<e<1\))的点的轨迹是椭圆。(即点\(P\)轨迹)
其中定点\(F\)为椭圆的焦点,定直线\(l\)称为椭圆的准线〈该定直线的方程是\(\displaystyle x=\pm \frac{a^{2}}{c}\)(焦点在\(x\)轴上),或\(\displaystyle y=\pm \frac{a^{2}}{c}\)(焦点在\(y\)轴上)〉。
如图:
推导过程:
已知\(\displaystyle P(x,y),|PF|=\sqrt{(x-c)^{2} +y^{2}} ,|PQ|=\frac{a^{2}}{c} -x,\)
\(\displaystyle \frac{|PF|}{|PQ|} =\frac{\sqrt{(x-c)^{2} +y^{2}}}{\frac{a^{2}}{c} -x} =e=\frac{c}{a} ,\)
注:\(\displaystyle \frac{c}{a} =e\) 是一个常数,即离心率
两边同时平方,整理得:
\(\displaystyle (1-\frac{c^{2}}{a^{2}} )x^{2} +y^{2} =a^{2} -c^{2}\) ...........\(\displaystyle Ⅰ,\)
目前已知:\(\displaystyle a^{2} =b^{2} +c^{2} ,\)
故\(\displaystyle 1-\frac{c^{2}}{a^{2}}\)可看成\(\displaystyle \frac{a^{2} -c^{2}}{a^{2}}\)即\(\displaystyle \frac{a^{2}}{b^{2}} ,\)
所以\(\displaystyle Ⅰ\)式可以化简为\(\displaystyle \frac{a^{2}}{b^{2}} x^{2} +y^{2} =b^{2} ,\)
即\(\displaystyle \frac{x^{2}}{a^{2}} +\frac{y^{2}}{b^{2}} =1,\)
得证.