PC算法详解-编程知识

PC算法详解

news/2024/11/14 8:50:13/文章来源:https://www.cnblogs.com/bleu/p/18412938

基于约束的方法(PC（Peter-Clark）算法)

基于约束的方法大多数是在经验联合分布上测试条件独立性，来构造一张反映这些条件独立性的图。通常会有多个满足一组给定的条件独立性的图，所以基于约束的方法通常输出一个表示某个 MEC（边缘计算）的图（例如，一个 PAG）。

最有名的算法是 PC 算法，

从一个完全无向图开始，通过条件独立性（d-separation）测试逐步去除边来识别骨架。
条件独立性测试用来评估 $X_i \perp \!\!\! \perp X_j|S$，其中条件集合S可能为空。
之后，如果骨架中存在一条 $X_i-X_k-X_j$ 这样的路径满足 $X_i\perp \!\!\! \perp X_j$ 但 $X_i\not\!\perp\!\!\!\perp X_j|X_k$ ，那么我们可以知道这条路径事实上一定是一个 v-结构，可以确定边的方向为 $X_i\rightarrow X_k\leftarrow X_j$ 。
在确定了所有 v-结构之后可以尝试给图中剩余的边确定方向，同时保持图的无环性，并尽量避免产生新的 v-结构。

算法伪代码步骤详解：

基于给定的顶点集V和条件独立性信息来估计一个骨架（skeleton）C以及可能的分离集S（这些分离集只在后续定向骨架时用得到）。

初始化：首先，基于顶点集V形成一个完全无向图C̃，这是所有可能边都存在的图。然后，初始化一个计数器λ为-1，并设置当前的骨架C为C̃。
外层循环：算法通过逐渐增加λ的值来迭代，每次迭代都尝试移除更多的边。λ代表考虑作为条件集k的元素数量的上限。
内层循环：对于每个λ值，算法遍历当前骨架C中所有相邻的顶点对(i, j)，但只考虑那些除了j之外，还有至少λ+1个邻居的顶点i（即|adj(C, i) \ {j}| ≥ λ）。
条件独立性测试：对于每一对这样的顶点i和j，算法尝试所有可能的子集k（从adj(C, i) \ {j}中选择，且|k| = λ），检查在给定k的条件下，i和j是否条件独立。
更新骨架：如果对于某个k，i和j是条件独立的，则从当前骨架C中删除边(i, j)，并将k保存到分离集S(i, j)和S(j, i)中。然后，尝试下一个可能的k，直到找到至少一个使i和j条件独立的k，或者尝试了所有可能的k。
终止条件：当对于所有相邻的顶点对(i, j)，|adj(C, i) \ {j}| < λ时，算法终止。这意味着在当前的λ值下，没有更多的边可以被删除。

通过逐步增加条件集k的大小（即λ的值），来更精确地确定哪些变量对在给定其他变量时是条件独立的。通过这种方式，可以逐步减少完全图中的边数，最终得到一个仅包含必要边的骨架图。

条件独立检验（d-分离）用这个结论公式来替换上面伪代码的第11行

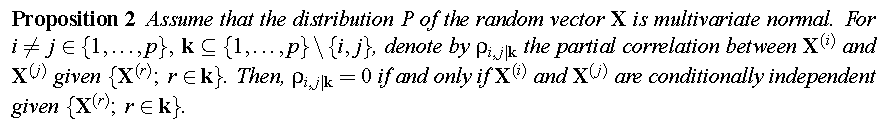
PC 算法采用了 Fisher Z Test作为条件独立性检验方法。实际上 Fisher Z Test 是一种相关性检验方法，但 PC 算法认为这一堆随机变量整体上服从多元高斯分布，这时“变量条件独立（没有相关性）”与“变量之间的偏相关系数为 0” 等价。

偏相关系数指校正其它变量后某一变量与另一变量的相关关系，校正的意思可以理解为假定其它变量都取值为均数。任意两个变量 $i, j$ 的 $h$ 阶（排除其他 $h$ 个变量的影响后， $h<=k-2$ ）偏相关系数为：$\rho_{i,j \mid K} = \frac{\rho_{i,j \mid K \backslash h} - \rho_{i,h \mid K \backslash h} \rho_{j,h \mid K \backslash h}}{\sqrt{(1 - \rho^2_{i,h \mid K \backslash h}) (1 - \rho^2_{j,h \mid K \backslash h})}}$

为了判断 $\rho$ 是否为 0，需要将 $\rho$ 通过 Fisher Z 变换转换成正态分布：$Z(i, j \mid K) = \frac{1}{2} \log (\frac{1 + \hat{\rho}_{i,j \mid K}}{1 - \hat{\rho}_{i,j \mid K}})$

定义零假设和对立假设：

零假设： $H_0(i,j \mid K): \rho_{i,j \mid K} = 0$，给定条件k下，变量i和j之间不存在条件相关性，即条件独立
对立假设： $H_A(i,j \mid K): \rho_{i,j \mid K} \not= 0$

然后给定一个显著性水平 $\alpha \in (0, 1)$ ，那么（双侧）检验的规则为，如果有：$\sqrt{n - |K| - 3}| Z(i,j \mid K) > \Phi^{-1} (1 - \alpha/2) $

其中 $\Phi(\cdot)$ 为 $\mathcal{N}(0, 1)$ 标准正态分布的累积分布函数CDF(norm.cdf)，则拒绝零假设，$i, k$ 关于 $K$ 条件相关。所以将上面伪代码的第 11 行替换成$\sqrt{n - |K| - 3}| Z(i,j \mid K) \leq \Phi^{-1} (1 - \alpha/2) $。

将骨架扩展到DAG的等价类CPDAG，需要用到上面的分离集S

初始化：从给定的骨架图Gskel和分离集S开始。
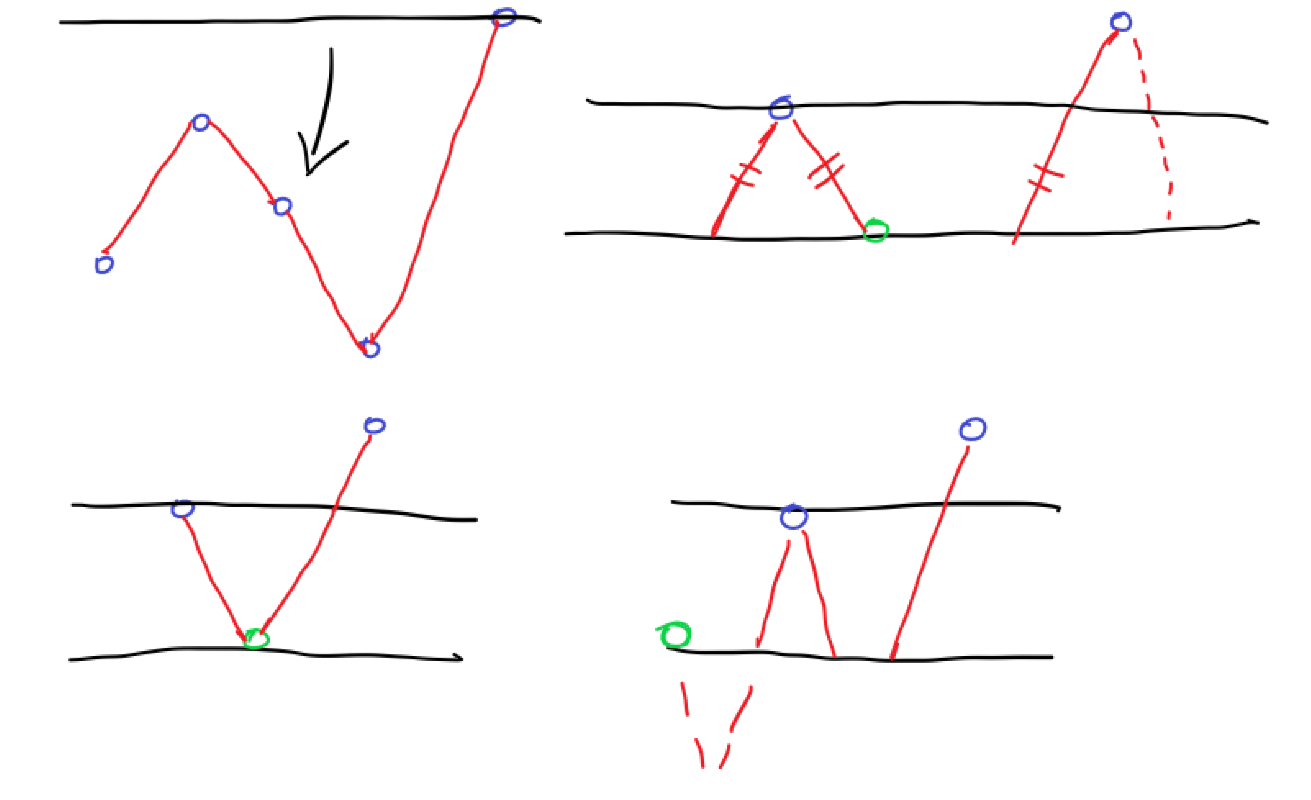
处理非邻接变量对：遍历所有在骨架图中非邻接但具有共同邻居k的变量对i, j。如果k不在i, j的分离集S(i, j)中（这个k的条件下不会使这两个i，j独立。只有对撞结构），则将i - k - j（其中-表示无向边）替换为i → k ← j（其中→表示有向边）。引入必要的有向边，尽可能找出所有对撞结构。
应用定向规则：在修改后的图中，通过反复应用以下规则来尽可能多地定向无向边：
- R1：如果存在有向边i → j，并且i和k是非邻接的，则将无向边j - k定向为j → k。（上面已经找出所有对撞，这里避免对撞）
- R2：如果存在链i → k → j，则将无向边i - j定向为i → j。（避免成环）
- R3：如果存在两条链i - k → j和i - l → j，其中k和l是非邻接的，则将无向边i - j定向为i → j。这个规则用于处理更复杂的依赖关系。（可以画图看看，只有当i→j时才能完全避免成环）
- R4（可选）：虽然通常不直接需要，但如果您希望包含这个规则，它表示如果存在两条链i - k → l和k → l → j，且k和l是非邻接的，则将无向边i - j定向为i → j。这个规则可以通过R3的多次应用来间接实现。
终止条件：当无法再应用任何规则来定向更多的无向边时，算法终止。