GYM 105350 E
题目描述
给定一个大小为 \(N\) 的数组 \(A\)。
我们定义一个大小为 \(N\) 的数组 \(B\) 是有效的当且仅当:
- 对于 \(\forall 1\le i\le N,1\le B_i \le N\),如果从 \(B\) 中移除 \(B_i\),则数组 \(B\) 恰好有 \(A_i\) 个不同的数。
求有多少个不同的由有效数组 \(B\) 组成的多重集合。
思路
分类讨论。
首先很容易想到,\(A\) 中至多有两种数字,且两种数字的差为 \(1\)。因为删除一个数字后不同数字数量至多减少一。否则输出 \(0\)。
- 若 \(A\) 中只有一个数字 \(x\),那么有两种情况:
- 如果 \(x=N-1\),那么有可能所有数互不相同,有 \(1\) 种情况。
- 如果 \(2x\le N\),那么有可能每个数的数量 \(\ge 2\),所以删掉哪个数都不变。这里要从 \(N\) 个数选出 \(x\) 个数用,并且每个数数量 \(\ge 2\) 且总和为 \(N\),根据插板法,有 \(C_{N-x-1}^{x-1}\cdot C_N^x\) 种情况。
- 若 \(A\) 中有两个数 \(x,x-1\),且 \(x-1\) 出现了 \(y\) 次,那么有三种情况:
- 若 \(x-y\le 0\),则无解,因为总共有 \(x\) 个数,其中有 \(y\) 个数出现了一次,所以无解。
- 若 \(2(x-y)+y>N\),则无解,因为有 \(x-y\) 个数至少出现 \(2\) 次,\(y\) 个数出现 \(1\) 次。
- 否则,我们要从 \(N\) 个数中选出 \(x-y\) 个数,再从 \(N-(x-y)\) 个数中选出 \(y\) 个数,同时那 \(x-y\) 个数每个数出现至少两次,且总共出现 \(N-y\) 次,通过插板法可知总共有 \(C_{N}^{x-y}\cdot C_{N-x+y}^y\cdot C_{N-x-1}^{x-y-1}\) 种情况。
空间复杂度 \(O(N)\),时间复杂度 \(O(N\log N)\)。
代码
#include<bits/stdc++.h>
using namespace std;const int MAXN = 300001, MOD = 998244353;int t, n, a[MAXN], cnt, f[MAXN], inv[MAXN], Inv[MAXN];void work() {f[0] = inv[1] = Inv[0] = 1;for(int i = 1; i < MAXN; ++i) {f[i] = 1ll * f[i - 1] * i % MOD;inv[i] = (i > 1 ? 1ll * (MOD - MOD / i) * inv[MOD % i] % MOD : 1);Inv[i] = 1ll * Inv[i - 1] * inv[i] % MOD;}
}int C(int n, int m) {return (n < m ? 0 : 1ll * f[n] * Inv[m] % MOD * Inv[n - m] % MOD);
}void Solve() {cin >> n;set<int> s;for(int i = 1; i <= n; ++i) {cin >> a[i];s.insert(a[i]);}if(s.size() > 2 || (s.size() == 2 && *s.begin() != *next(s.begin()) - 1)) {cout << "0\n";return;}cnt = 0;for(int i = 1; i <= n; ++i) {cnt += (a[i] == *s.begin());}if(s.size() == 1) {int ans = (*s.begin() == n - 1), res = *s.begin();if(2 * res <= n) {ans = (ans + 1ll * C(n - res - 1, res - 1) * C(n, res) % MOD) % MOD;}cout << ans << "\n";}else {int res = *next(s.begin()) - cnt;if(res <= 0 || 2 * res + cnt > n) {cout << "0\n";return;}cout << 1ll * C(n - cnt - res - 1, res - 1) * C(n, res) % MOD * C(n - res, cnt) % MOD << "\n";}
}int main() {ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);work();for(cin >> t; t--; Solve()) {}return 0;
}
GYM 105350 F
题目描述
我们定义一个数组 \(B\) 的 \(\operatorname{MAD}(B)\) 为至少出现两次的最大值,如果没有数出现两次,则 \(\operatorname{MAD}(B)=0\)。
给定数组 \(A\),求 \(\sum \limits_{l=1}^{N-1}\sum\limits_{r=l+1}^N \operatorname{MAD}([A_l,A_{l+1},\dots,A_r])\)。
思路
我们考虑固定 \(r\),看对应的 \(l\) 和其 \(\operatorname{MAD}\)。图像如下:
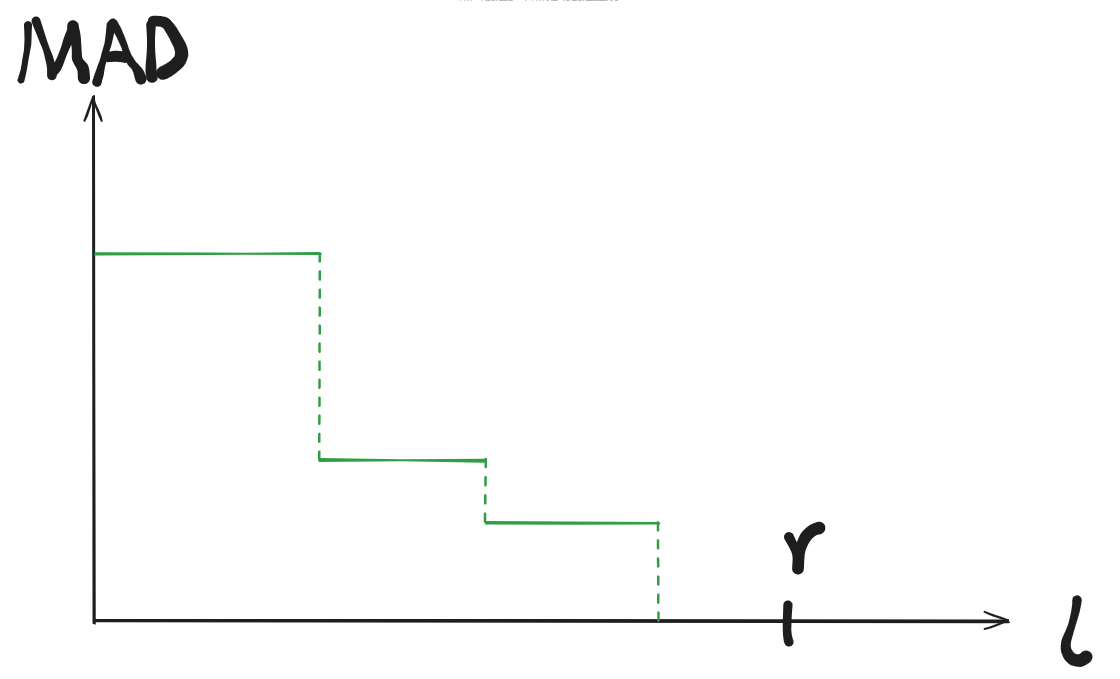
接着我们考虑转移到 \(r+1\):
这里高出来了蓝色部分是因为 \(A_{r+1}\) 变得出现了两次,所以在这里会增加 \(\operatorname{MAD}\) 的值。这个很显然能用线段树维护。
空间复杂度 \(O(N)\),时间复杂度 \(O(N\log N)\)。
代码
#include<bits/stdc++.h>
using namespace std;
using ll = long long;const int MAXN = 200001;struct Segment_Tree {int l[MAXN << 2], r[MAXN << 2], lazy[MAXN << 2], id[MAXN << 2], Min[MAXN << 2];ll sum[MAXN << 2];void build(int u, int s, int t) {l[u] = s, r[u] = t, sum[u] = Min[u] = lazy[u] = 0;if(s == t) {id[u] = s;return;}int mid = (s + t) >> 1;build(u << 1, s, mid), build((u << 1) | 1, mid + 1, t);}void tag(int u, int x) {sum[u] = max(sum[u], 1ll * x * (r[u] - l[u] + 1)), Min[u] = max(Min[u], x), lazy[u] = max(x, lazy[u]);}void pushdown(int u) {tag(u << 1, lazy[u]), tag((u << 1) | 1, lazy[u]), lazy[u] = 0;}void update(int u, int s, int t, int x) {if(s > t) {return;}if(l[u] >= s && r[u] <= t) {tag(u, x);return;}pushdown(u);if(s <= r[u << 1]) {update(u << 1, s, t, x);}if(t >= l[(u << 1) | 1]) {update((u << 1) | 1, s, t, x);}sum[u] = sum[u << 1] + sum[(u << 1) | 1];Min[u] = min(Min[u << 1], Min[(u << 1) | 1]);}int Binary_Search(int u, int x) {if(Min[u] >= x) {return 1919810;}if(l[u] == r[u]) {return id[u];}pushdown(u);if(Min[u << 1] < x) {return Binary_Search(u << 1, x);}return Binary_Search((u << 1) | 1, x);}ll Getsum(int u, int s, int t) {if(s > t) {return 0ll;}if(l[u] >= s && r[u] <= t) {return sum[u];}pushdown(u);return (s <= r[u << 1] ? Getsum(u << 1, s, t) : 0ll) + (t >= l[(u << 1) | 1] ? Getsum((u << 1) | 1, s, t) : 0ll);}
}tr;int t, n, a[MAXN];
ll ans;
map<int, int> id;void Solve() {cin >> n;for(int i = 1; i <= n; ++i) {cin >> a[i];}tr.build(1, 1, n);id.clear();ans = 0;for(int i = 1; i <= n; ++i) {if(id.count(a[i])) {tr.update(1, tr.Binary_Search(1, a[i]), id[a[i]], a[i]);}ans += tr.Getsum(1, 1, i);id[a[i]] = i;}cout << ans << "\n";
}int main() {ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);for(cin >> t; t--; Solve()) {}return 0;
}
GYM 105350 G
题目描述
给定一个大小为 \(N\),以 \(1\) 为根的树。最开始,所有结点的权值均为 \(0\)。有以下四种操作:
- 令 \(u\) 子树内所有权值加 \(x\)。
- 令 \(u\) 所有儿子权值加 \(x\)。
- 查询 \(u\) 子树内权值最大值。
- 查询 \(u\) 所有儿子权值最大值。
思路
由于在 dfs 序中一个结点的儿子是不连续的,所以我们考虑调整一下这个 dfs 序:
- 当递归到结点 \(u\) 时,我们先把它的所有儿子丢进 dfs 序里。
- 然后递归到它的所有儿子里。
这样很明显儿子就是连续的了,但子树却不一定连续。但通过观察可以发现,子树最多会被分成两个部分:根节点和除了根节点的部分。
所以使用线段树维护即可。
空间复杂度 \(O(N+M)\),时间复杂度 \(O(Q\log N)\)。
代码
#include<bits/stdc++.h>
using namespace std;
using ll = long long;const int MAXN = 300005;struct Segment_Tree {int l[MAXN << 2], r[MAXN << 2];ll Max[MAXN << 2], lazy[MAXN << 2];void build(int u, int s, int t) {l[u] = s, r[u] = t, Max[u] = lazy[u] = 0;if(s == t) {return;}int mid = (s + t) >> 1;build(u << 1, s, mid), build((u << 1) | 1, mid + 1, t);}void tag(int u, ll x) {Max[u] += x, lazy[u] += x;}void pushdown(int u) {tag(u << 1, lazy[u]), tag((u << 1) | 1, lazy[u]), lazy[u] = 0;}void update(int u, int s, int t, ll x) {if(s > t) {return;}if(l[u] >= s && r[u] <= t) {tag(u, x);return;}pushdown(u);if(s <= r[u << 1]) {update(u << 1, s, t, x);}if(t >= l[(u << 1) | 1]) {update((u << 1) | 1, s, t, x);}Max[u] = max(Max[u << 1], Max[(u << 1) | 1]);}ll Getmax(int u, int s, int t) {if(s > t) {return -(ll)(1e18);}if(l[u] >= s && r[u] <= t) {return Max[u];}pushdown(u);return max((s <= r[u << 1] ? Getmax(u << 1, s, t) : -(ll)(1e18)), (t >= l[(u << 1) | 1] ? Getmax((u << 1) | 1, s, t) : -(ll)(1e18)));}
}tr;int n, q, dfn[MAXN], sz[MAXN], st[MAXN], End[MAXN], tot = 1;
vector<int> e[MAXN];void dfs(int u, int fa) {sz[u] = 1, st[u] = tot + 1;for(int v : e[u]) {if(v != fa) {dfn[v] = ++tot;}}End[u] = tot;for(int v : e[u]) {if(v != fa) {dfs(v, u);sz[u] += sz[v];}}
}int main() {ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);cin >> n >> q;for(int i = 1, u, v; i < n; ++i) {cin >> u >> v;e[u].emplace_back(v);e[v].emplace_back(u);}tr.build(1, 1, n);dfn[1] = 1;dfs(1, 0);for(int i = 1, op, u, x; i <= q; ++i) {cin >> op >> u;if(op == 1) {cin >> x;tr.update(1, dfn[u], dfn[u], x), tr.update(1, st[u], st[u] + sz[u] - 2, x);}else if(op == 2) {cin >> x;tr.update(1, st[u], End[u], x);}else if(op == 3) {cout << max(tr.Getmax(1, st[u], st[u] + sz[u] - 2), tr.Getmax(1, dfn[u], dfn[u])) << "\n";}else if(op == 4) {cout << tr.Getmax(1, st[u], End[u]) << "\n";}}return 0;
}
AT AGC023 F
题目描述
给定一个 \(N\) 个结点的树,每个结点上都有一个数字 \(0\) 或 \(1\)。你要将这些点排成一行,使得没有结点在其祖先之前。求这些节点上数的最小逆序对数量。
思路
我们考虑把哪个数放在前面更优