龙(dragon)
难点:
(1)删边后如何寻找新的最短路。
(2)A,B两方的决策互相影响十分复杂。
(3)如何统计每个起点的ans。
解题:
(3)解决这类多起点一终点的问题,可以想到dp。
(1)解决这类最短路转移的问题,可以考虑最短路树。
(2)解决这类博弈问题,可以设计两个dp数组,分别维护影响前后的ans,在转移到最终的答案数组。
拆除炸弹(youyou)
难点:
(1)如何维护与判断一个二分图(没有奇环)。
(2)维护一个区间并要将其排序,时间复杂度大。
(3)区间内含有的信息量过大。
解题:
(1)判断二分图,可以用并查集。
(2)需要维护并排序区间,可以用线段树,但要注意信息量与合并复杂度。
(3)对于这类问题,可以:1.对部分信息记忆化并离线改变区间的查询顺序。2.分析性质去掉无用信息。
(3‘)关于并查集(树)的连通性问题,只有n-1条树边起关键作用。
赖教(lai)
难点:
(1)“赖教”势力的扩散不好处理。
(2)使最终的“赖教”消失难维护。
(3)如何使军队花费最优。
解题:
(1)对于这类会扩散的问题,可以逆思考空区间的缩减,并将其绘成形如等腰三角的图。
(2)使最终无法扩散,即"赖教"消失,会发现就是诸多等腰三角形的拼接清空完1到n。
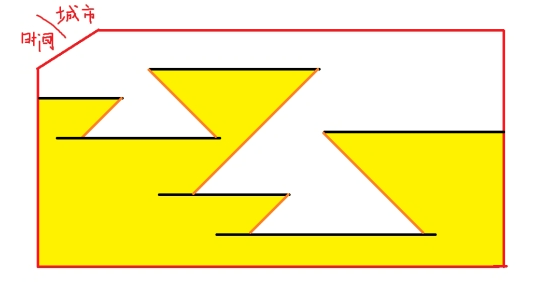
(3)区间覆盖的最优性问题,可以考虑最短路算法(以区间为点的点去最短路)。
(3‘)点去最短路寻找出度困难时,可以使用







![AT_arc184_d [ARC184D] Erase Balls 2D](https://cdn.luogu.com.cn/upload/image_hosting/66p2a0rv.png)