在这
权当卡特兰数的复习题吧。不会卡特兰数的可以先看文末。
如果没有花色 \(1\) 这道题就很简单了,对于每个别的花色都有 \(C(m)\) 种分配方案。\(C(n)\) 表示卡特兰数的第 \(n\) 项,答案就是乘起来。
发现除了花色 \(1\) 每种花色的牌都是独立的。这启示我们枚举每种牌用了多少张花色 \(1\)。设 \(f_{i,j}\) 表示前 \(i\) 种花色的牌用了 \(j\) 张花色 \(1\) 能使第一名玩家获胜的方案数。
有转移:
枚举的 \(k\) 的含义为第 \(i\) 个花色用了 \(k\) 张花色 \(1\)。其中 \(H(k)\) 表示用了 \(k\) 张花色 \(1\) 的分配方案。
\(H(k)\) 的计算也是简单的,考虑卡特兰数的经典问题,不能经过直线 \(y=x\) 的方格路计数(如果不会可以看文末)。我们先得到了 \(k\) 张极大的牌,可以看做在网格中先向右走了 \(k\) 步,那问题就成了从 \((0,k)\) 走到 \((\frac{m+k}{2},\frac{m+k}{2})\) 且不能经过直线 \(y=x\) 的方案数。
答案就是:
至此,已经解决大部分问题了,最后就是解决花色 \(1\) 的分配。上面的问题是 \(m\) 张牌中需要先拿出 \(k\) 张与花色 \(1\) 匹配,而现在的问题是 \(m\) 张花色 \(1\) 需要拿出若干张与其他牌匹配,发现问题是一样的,统计答案时乘上 \(H(k)\) 就好了,这里的 \(k\) 表示有 \(k\) 张花色 \(1\) 被用来与其他花色的牌匹配。
复杂度为 \(O(n^3)\),如果你是大常数选手就会 TLE,有一个优化是 \(\frac{m+k}{2}\) 为整数的状态才合法,加上这个就不卡常了。
#include <bits/stdc++.h>using namespace std;const int maxN = 1e3 + 7, mod = 998244353;int fc[maxN], ifc[maxN];
int ksm(int a, int b = mod - 2) {int res = 1;while (b) {if (b & 1)res = 1ll * res * a % mod;a = 1ll * a * a % mod;b >>= 1;}return res;
}int n, m;int C(int n, int m) {if (n < 0 || m < 0 || n < m) return 0;return 1ll * fc[n] * ifc[m] % mod * ifc[n - m] % mod;
}
int H(int k) {auto res = C(m, (m + k) / 2) - C(m, (m + k) / 2 + 1);res += res < 0 ? mod : 0;return res;
}int f[507][507];signed main() {ios::sync_with_stdio(false), cin.tie(nullptr);cin >> n >> m;fc[0] = 1;for (int i = 1; i <= m * 2; i++)fc[i] = 1ll * fc[i - 1] * i % mod;ifc[m * 2] = ksm(fc[m * 2]);for (int i = m * 2 - 1; i >= 0; i--)ifc[i] = 1ll * ifc[i + 1] * (i + 1) % mod;f[1][0] = 1;for (int i = 2; i <= n; i++)for (int j = 0; j <= m; j++)for (int k = (m & 1); k <= j; k += 2)f[i][j] = (f[i][j] + 1ll * f[i - 1][j - k] * H(k) % mod) % mod;int ans = 0;for (int k = 0; k <= m; k++)ans = (ans + 1ll * f[n][k] * H(k) % mod) % mod;cout << ans << '\n';
}
卡特兰数可以解决这类问题:有一个大小为 \(n\times n\) 的方格图左下角为 \((0, 0)\) 右上角为 \((n, n)\) ,从左下角开始每次都只能向右或者向上走一单位,不走到对角线 \(y=x\) 上方(但可以触碰)的情况下到达右上角有多少可能的路径?(摘自 OI Wiki)
答案就是所有的路径数减去不合法的路径数,发现不合法的路径一定经过直线 \(y=x+1\)。对于经过 \(y=x+1\) 且终点为 \((n,n)\) 的路径,在它第一次接触 \(y=x+1\) 后,把它的所有运动反向,向右走变为向上走,向上走变为向右走,最后它一定会到达 \((n-1,n+1)\)。
下图中的橙色虚线和粉色虚线是不合法的路径。
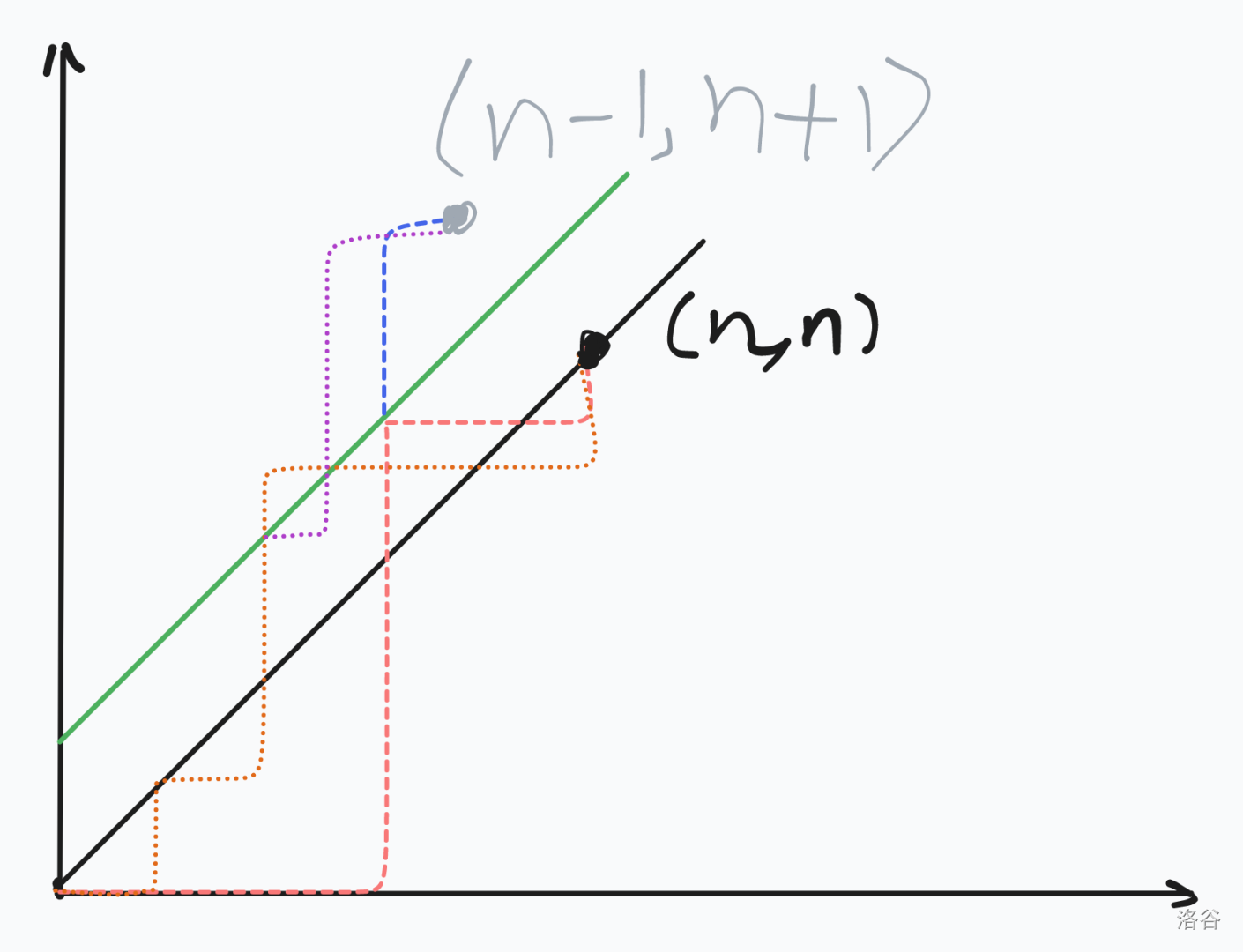
可以得出 \(C(n)\) 为从 \((0,0)\) 到 \((n,n)\) 的路径数减从 \((0,0)\) 到 \((n-1,n+1)\) 的路径数。
所以: