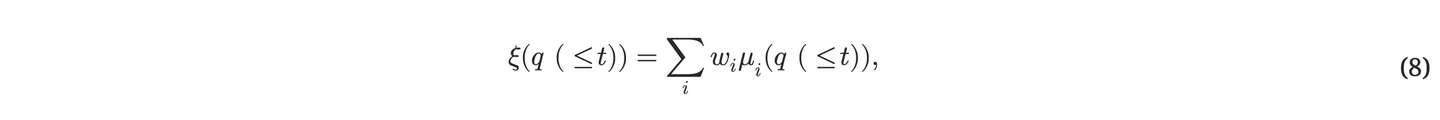Cut the Sequence

Cut the Sequence

P10977 Cut the Sequence

前言

单调队列优化 dp 的好题，思维难度大细节多。因为觉得自己看不懂其他题解，在看完 y 总的讲解后豁然开朗，所以写这篇题解来巩固一下。包括完整的细节分析和思考过程，或许很多大佬都不需要 qwq。叠甲完毕，下面开始正文。

分析

先考虑无解的情况，将单个元素分成段，每段的和最小，如果还是大于 \(m\) 肯定无解。所以当存在 \(a_i > m\) 时，输出 \(-1\)。

状态表示

题意和给出的信息都很简单，看 \(n\) 的范围判断大致是 \(O(n)\) 或者 \(O(n\log(n))\) 的算法。因为要满足限制且最优化答案，不难想到动态规划来解决。第一维显然是考虑前 \(i\) 个数，通过复杂度分析判断不能存在第二维，实际上也并不需要。所以，设 \(f_i\) 表示只考虑前 \(i\) 个数划分成若干段，每段的和不超过 \(m\) 的最小代价，代价为每一段的最大值之和。

状态转移

考虑 \(f_i\) 的集合划分依据，显然是最后一段的长度，设上一个状态为 \(f_j\)，最后一段就是 \([j+1,i]\)，其中 \(0 \le j \le i-1\)，而且要满足限制，所以 \(\sum_{k=j+1}^{i} a_k \le m\)，最后一段产生的贡献为 \(\max_{k=j+1}^{i} a_k\)。状态转移方程即为：

\[ f_i=\min_{0 \le j \le i-1 \land \sum_{k=j+1}^{i} a_k \le m} (f_j+\max_{k=j+1}^{i} a_k) \]

优化

上面这个方程显然是 \(O(n^2)\) 的，不足以通过此题。看式子好像也没啥能转化的，考虑一些性质来优化。

首先注意到 \(f\) 是单调不减的，也就是说 \(f_{i-1} \le f_i\)，简单证明下：

设最后一段的贡献为 \(a_{max}\)，考虑在末尾加上 \(a_i\)。

• 若 \(a_i\) 加入最后一段，
  • \(a_i > a_{max}\) 时，有 \(f_i=f_{i-1}-a_{max}+a_i\)。
  • \(a_i \le a_{max}\) 时，有 \(f_i=f_{i-1}\)。
• 若 \(a_i\) 自己新开一段，有 \(f_i=f_{i-1}+a_i\)。

因为序列中的数大于等于 \(0\)，所以有 \(f_{i-1} \le f_i\)，即 \(f\) 单调不减。

蓝书上的话：

DP 转移优化的指导思想就是及时排除不可能的决策，保持候选集合的高度有效性和秩序性。

所以不妨设 \(j\) 为转移的最优决策，考虑其满足什么样的性质。

\[ f_i=\min(f_j+a_{max}) \]

设最后一段的贡献为 \(a_{max}\)，设 \(k_0\) 为满足 \(\sum_{k=j+1}^{i} a_k \le m\) 的最小的 \(j\)。\(a_{max_1}\) 为 \([k_0,i]\) 的最大值，下标为 \(k_1\)。次大值为 \(a_{max_2}\)，下标为 \(k_2\)。所以：

\[ \max_{k=k_0+1}^{i} a_k=a_{max_1}=a_{k_1} \]

\[ \max_{k=k_1+1}^{i} a_k=a_{max_2}=a_{k_2} \]

\[ \max_{k=k_2+1}^{i} a_k=a_{max_3}=a_{k_3} \]

\[ \dots \]

• 当 \(k_0 \le j < k_1\) 时，\(a_{max}=a_{max_1}\)，\(f_j\) 最小值肯定是在 \(j=k_0\) 时，所以最优的 \(j\) 为 \(k_0\)。
• 当 \(k_1 \le j < k_2\) 时，\(a_{max}=a_{max_2}\)，最优的 \(j\) 为 \(k_1\)。
• 当 \(k_2 \le j < k_3\) 时，\(a_{max}=a_{max_3}\)，最优的 \(j\) 为 \(k_2\)。

所以最优决策 \(j\) 为 \(k_0,k_1,k_2,\dots\)

所以 \(j\) 要成为最优决策，除了要满足 \(\sum_{k=j+1}^{i} a_k \le m\) 外，还要满足下面条件之一：

1. 取 \(k_0\) 时，\(k_0\) 为满足 \(\sum_{k=j+1}^{i} a_k \le m\) 的最小的 \(j\)。
2. 取 \(k_1,k_2,k_3,\dots\) 时，满足 \(a_j=\max_{k=j}^{i} a_k\)。

情况 \(1\)，只需要用双指针求 \(k_0\)。

情况 \(2\)，可以用单调队列维护 \(k_1,k_2,\dots\)，只需要保证 \(a_j\) 单调递减。可是有一个问题，\(f_j+a_{max}\) 在单调队列中并不一定是单调的，所以要用其他东西维护，要支持加入元素，删除元素，求最小值，可以用平衡树，当然不用自己写，可以用 set，但是值可能有重复，所以使用 multiset。\(k_p\) 为队列中的元素，能产生的贡献为 \(f_{k_p}+a_{k_{p+1}}\)

有一个细节，只有当单调队列中的元素大于一时，才能出现第二种情况，思考一下就能理解。

code

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>
#include <queue>
#include <map>
#include <set>
using namespace std;
typedef long long ll;
const int N=1e5+5;
int n;
ll m;
ll a[N],f[N];
int q[N];
multiset<ll> st;
void solve()
{cin>>n>>m;for(int i=1;i<=n;i++){cin>>a[i];if(a[i]>m) //无解的情况{cout<<"-1\n";return ;}}int l=1,r=0;ll sum=0;for(int i=1,j=1;i<=n;i++){sum+=a[i];while(sum>m) {sum-=a[j++];while(l<=r&&q[l]<j) {if(l<r) st.erase(f[q[l]]+a[q[l+1]]);l++;}}while(l<=r&&a[q[r]]<=a[i]) {if(l<r) st.erase(f[q[r-1]]+a[q[r]]);r--;}q[++r]=i;if(l<r) st.insert(f[q[r-1]]+a[q[r]]);f[i]=f[j-1]+a[q[l]];//处理后j=k0+1if(st.size()) f[i]=min(f[i],*st.begin());}cout<<f[n]<<'\n';
}
int main()
{#ifndef ONLINE_JUDGEfreopen("1.in","r",stdin);freopen("1.out","w",stdout);#endif ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);solve();return 0;
}