qoj7301
orz yxx
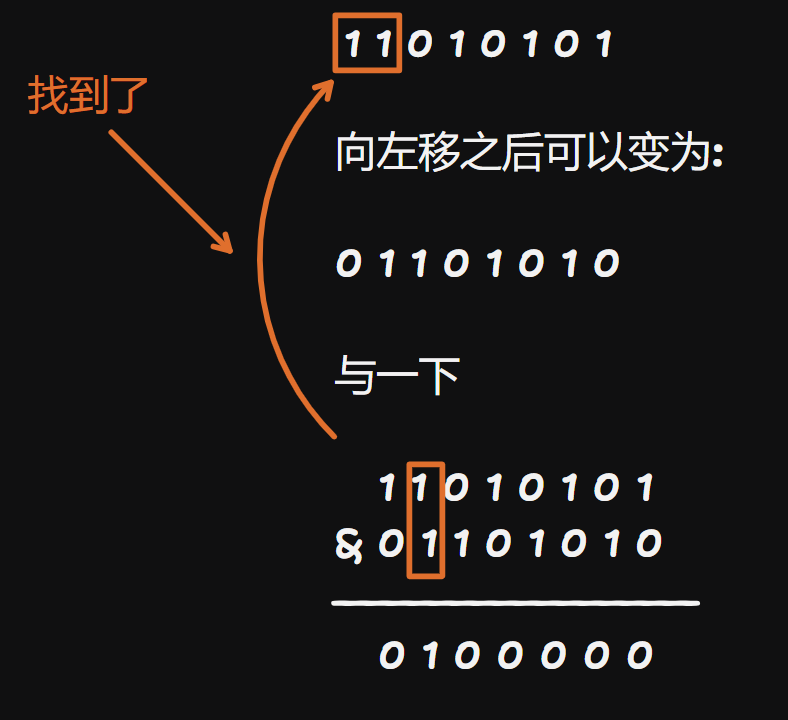
有一个很牛的状态设计 \(f_{i,j,0/1}\),\(0\) 为 \(a_{i-1}>a_i\),\(j\) 记录 \(a_{i-1}\) 的值,\(a_i\) 的值未定;\(1\) 为 \(a_{i-1}<a_i\),\(j\) 记录 \(a_i\) 的值
这样可以完美解决 \(a_{i-1}>a_i<a_{i+1}\) 的问题
转移和优化都是简单的,时间复杂度 \(O(n^2)\),思想是:不需要用的东西就可以暂时不记录
submission
AGC036D
牛!
首先的一个发现是:如果保留负边 \(i\to j(i<j)\),则一定会保留 \(i'\le i,j'\ge j\),\(i'\to j'\) 的所有负边
原因是 \(i'\to j'\) 等价于从 \(i'\) 先走 \(0\) 边到 \(i\),再走 \(i\to j\),最后走 \(j\to j'\) 的 \(0\) 边
这个性质仍然不够强!
这里给出更强的性质:我们一定可以把序列划分成若干个不交的区间,删除同一区间内的负边和跨过 \(\ge 2\) 个区间的正边
即形如:
我们来口胡一个证明:
令 \(i\) 往右第一条负边为 \(i\to r_i\)
如果出现 \(i<j<r_i<r_j\),我们证明一定可以加入边 \(j\to r_i\)
如果 \(r_p=i\) 和 \(r_q=j\) 的 \(p,q\) 集合完全相同的话(即最大的 \(p=\) 最大的 \(q\)),那么显然不会影响;否则我们可以找到一额子问题 \(p<q<r_p<r_q\),继续规约下去
后面的 \(dp\) 就好做了,直接做就是 \(O(n^3)\) 的
submission