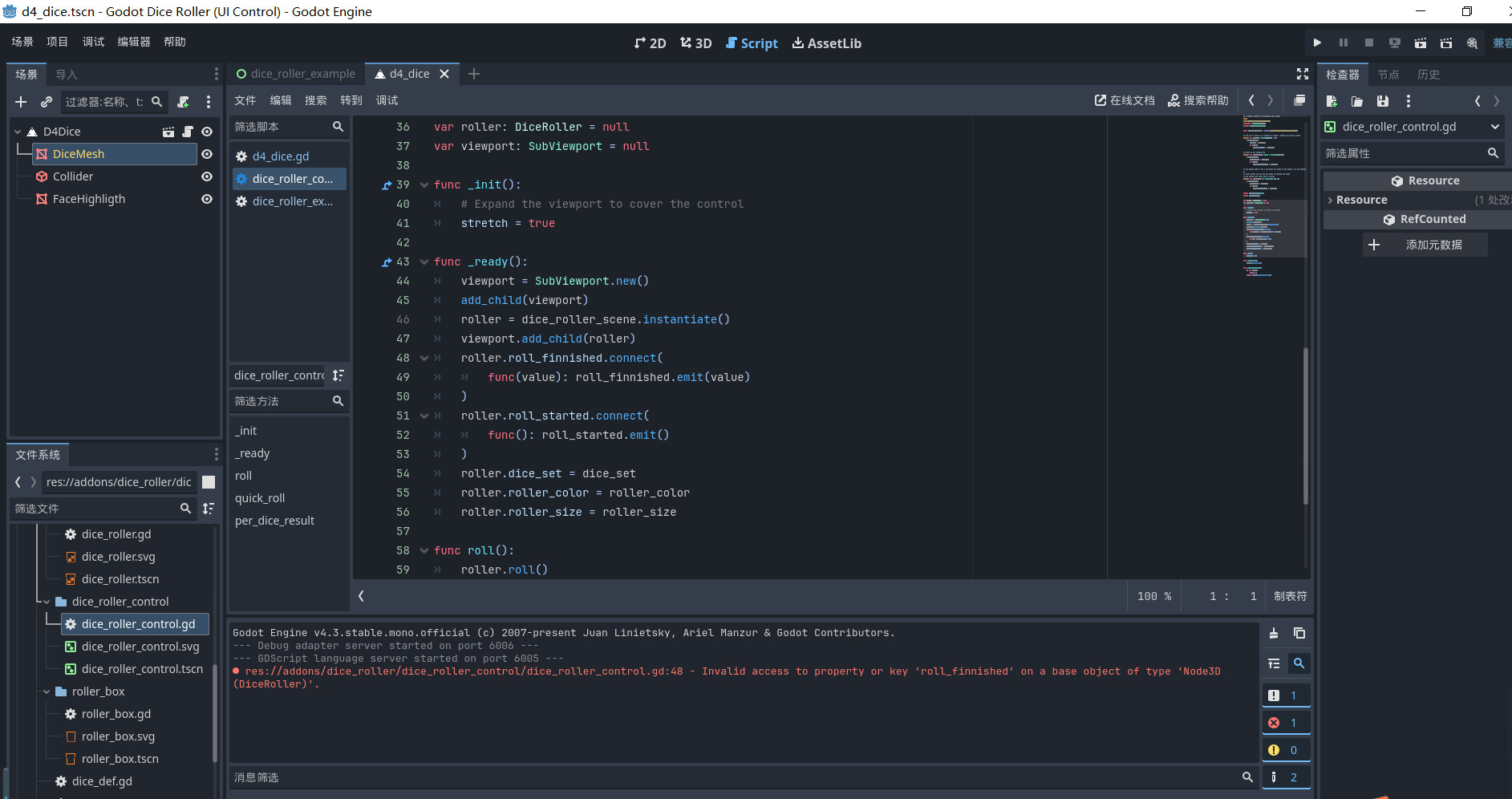
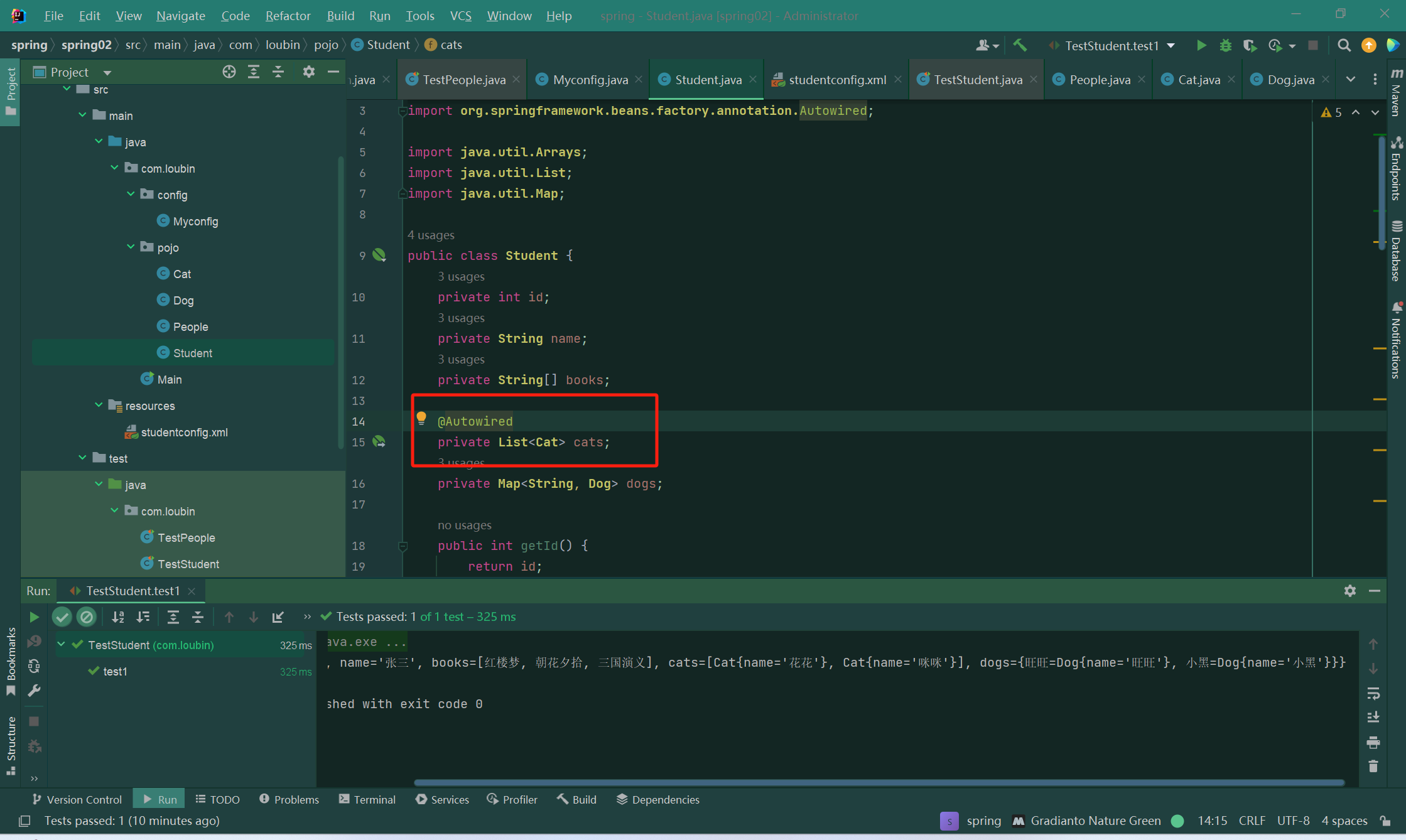
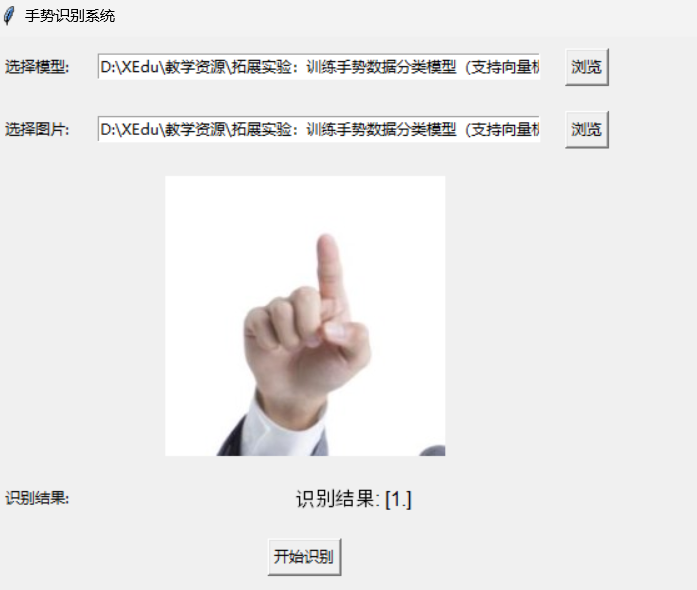
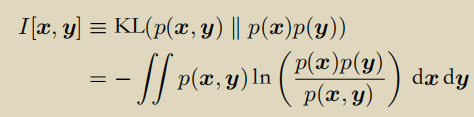考虑如果没有修改,用 ST 表就非常舒服。
考虑暴力修改,需要修改所有覆盖了这个位置的区间,时间复杂度是 \(O(n)\) 的。
而如果只修改 \(\frac{\log n}{2}\) 层,时间复杂度就是 \(O(\sqrt{n})\) 的。查询时从上往下查,最多查到第 \(\frac{\log n}{2}\) 层,时间复杂度就也是 \(O(\sqrt{n})\) 的。于是就可以通过。
#include<bits/stdc++.h>
#define ll long long
#define il inlineusing namespace std;
namespace asbt{
namespace cplx{bool begin;}
const int maxn=2e5+5;
int n,m,blen,st[maxn][20];
il int Log(int x){if(x==1){return 0;}return Log(x>>1)+1;
}
il void upd(int l,int k){if(k==blen){return ;}if(l-(1<<k)>0){st[l-(1<<k)][k+1]=abs(st[l-(1<<k)][k]-st[l][k]);upd(l-(1<<k),k+1);}if(l+(1<<(k+1))-1<=n){st[l][k+1]=abs(st[l][k]-st[l+(1<<k)][k]);upd(l,k+1);}
}
il int query(int l,int k){if(k<=blen){return st[l][k];}return abs(query(l,k-1)-query(l+(1<<(k-1)),k-1));
}
namespace cplx{bool end;il double usdmem(){return (&begin-&end)/1048576.0;}
}
int main(){ios::sync_with_stdio(0),cin.tie(0);cin>>n>>m;for(int i=1;i<=n;i++){cin>>st[i][0];}blen=Log(n)>>1;for(int j=1;j<=blen;j++){for(int i=1;i+(1<<j)-1<=n;i++){st[i][j]=abs(st[i][j-1]-st[i+(1<<(j-1))][j-1]);}}while(m--){int opt,l,k;cin>>opt>>l>>k;if(opt==1){st[l][0]=k;upd(l,0);}else{cout<<query(l,k)<<"\n";}}return 0;
}
}
int main(){return asbt::main();}