一、本周内容总结
本周主要进行了蓝桥和天梯的训练,训练了3场蓝桥、2场天梯,剩余时间的就是赛后补题
补题的过程也重新理清了很多知识,包括gcd和lcm的应用,多项式除法的过程等等
对于蓝桥和天梯的赛制,还重新背了下很多算法的板子,包括求最短路的多种方法,不同范围求组合数,求最近公共祖先等等
二、补题
2.17 蓝桥训练1

C-[蓝桥杯 2013 国 AC] 网络寻路
思路:比较简单的方法是用度来计算,要计算A-B-C-D的个数,可以枚举B-C,这类路径的个数为(B的度数-1)*(C的度数-1)
void solve() {int n, m;cin >> n >> m;vector<int> d(n + 1);vector<PII> ve(m);for (int i = 0; i < m; ++i) {int u, v;cin >> u >> v;ve[i] = {u, v};d[u] ++, d[v] ++;}int ans = 0;for (int i = 0; i < m; ++i) {int u = ve[i].first, v = ve[i].second;if (u == v) continue;ans += (d[u] - 1) * (d[v] - 1) * 2;}cout << ans;
}D-[传智杯 #4 初赛] 小卡和质数
思路:只有奇数与偶数异或值可能为1,且偶数只有2为质数,说明只存在1和2这种情况是YES
E-[蓝桥杯 2020 国 C] 重复字符串
思路:贪心,统计每段字符串对应的相同位置的字符的种类个数,每个位置修改为种类出现最对的字符
void solve() {int k;cin >> k;string s;cin >> s;int n = s.size();s = ' ' + s;if (n % k != 0) cout << "-1";else {int m = n / k, ans = 0;vector<vector<int> > cnt(m, vector<int>(30, 0));for (int i = 0; i < k; ++i) {for (int j = 1; j <= m; ++j) {int u = i * m + j;int v = s[u] - 'a' + 1;cnt[j - 1][v] ++;cnt[j - 1][0] = max(cnt[j - 1][0], cnt[j - 1][v]);}}for (int i = 0; i < m; ++i) ans += k - cnt[i][0];cout << ans;}
}F-[蓝桥杯 2024 省 B] 宝石组合
思路:
知道了以上求gcd和lcm的式子后,对于
可以对每个p单独处理,得到
现在要求最大的S,数的范围为1e5,可以找出Hi的因子,统计每种因子对应的Hi,枚举答案S,若S对应的H个数存在3个即为答案
void solve() {int n;cin >> n;vector<int> h(n + 1);vector<vector<int> > cnt(N);for (int i = 1; i <= n; ++i) {cin >> h[i];for (int j = 1; j * j <= h[i]; ++j) {if (h[i] % j == 0) {cnt[j].push_back(h[i]);if (h[i] / j != j) cnt[h[i] / j].push_back(h[i]);}}}for (int i = N - 1; i >= 1; --i) {if (cnt[i].size() > 2) {std::sort(cnt[i].begin(), cnt[i].end());for (int j = 0; j < 3; ++j) cout << cnt[i][j] << ' ';return ;}}
}G-[蓝桥杯 2022 国 A] 环境治理
思路:二分+最短路
二分答案,且n的范围为100,可以用floyd求最短路
void solve() {int n, q;cin >> n >> q;vector<vector<int>> val(n + 1, vector<int>(n + 1));vector<vector<int>> L(n + 1, vector<int>(n + 1));for (int i = 1; i <= n; ++i)for (int j = 1; j <= n; ++j) cin >> val[i][j];for (int i = 1; i <= n; ++i)for (int j = 1; j <= n; ++j) cin >> L[i][j];int l = 0, r = 1e7, ans = -1;auto check = [&](int x) {vector<int> sub(n + 1);int add = x % n;for (int i = 1; i <= n; ++i) {sub[i] = x / n;if (add) sub[i] ++, add --;}vector<vector<int> > dis = val;for (int i = 1; i <= n; ++i) {for (int j = i + 1; j <= n; ++j) {dis[i][j] = max(L[i][j], dis[i][j] - sub[i] - sub[j]);dis[j][i] = dis[i][j];}}for (int k = 1; k <= n; ++k) {for (int i = 1; i <= n; ++i) {for (int j = 1; j <= n; ++j) {if (dis[i][j] > dis[i][k] + dis[k][j]) dis[i][j] = dis[i][k] + dis[k][j];}}}int res = 0;for (int i = 1; i <= n; ++i) {for (int j = 1; j <= n; ++j) {res += dis[i][j];}}return res <= q;};while (l <= r) {int mid = l + r >> 1;if (check(mid)) r = mid - 1, ans = mid;else l = mid + 1;}cout << ans;
}I-[蓝桥杯 2018 国 B] 搭积木
思路:dp+优化
首先很明显想到dp,f[i][l][r]表示第i层积木区间为[l, r]的方案数,枚举x≤l,y≥r,转移式子为f[i][l][r] = ∑f[i-1][x][y]
此时的复杂度是nm4的
考虑在求 ∑f[i-1][x][y]处优化,可以预处理出二维前缀和,pre[x][y]=∑f[i-1][i][j](i≤x,j≤y)
即f[i][l][r] = ∑f[i-1][x][y]可以转换为求1≤x≤l,r≤y≤m的二维区间和,f[i][l][r] = pre[l][m] - pre[l][r - 1] - pre[0][m] + pre[0][r - 1]
int f[N][N][N], pre[N][N];
void solve() {int n, m;cin >> n >> m;vector<string> ve(n + 1);for (int i = n; i >= 1; --i){cin >> ve[i];ve[i] = ' ' + ve[i];}int ans = 1;f[0][1][m] = 1;for (int l = 1; l <= m; ++l)for (int r = 1; r <= m; ++r) pre[l][r] = (pre[l - 1][r] + pre[l][r - 1] - pre[l - 1][r - 1] + f[0][l][r] + Mod) % Mod;for (int i = 1; i <= n; ++i) {for (int l = 1; l <= m; ++l) {for (int r = l; r <= m; ++r) {if (ve[i][r] == 'X') break;f[i][l][r] = (pre[l][m] - pre[l][r - 1] - pre[0][m] + pre[0][r - 1] + Mod) % Mod;ans = (ans + f[i][l][r]) % Mod;}}for (int l = 1; l <= m; ++l)for (int r = 1; r <= m; ++r) pre[l][r] = (pre[l - 1][r] + pre[l][r - 1] - pre[l - 1][r - 1] + f[i][l][r] + Mod) % Mod;}cout << ans;
}J-[蓝桥杯 2024 省 B] 拔河
思路:
n的范围为1e3,用multiset维护所有区间和,从小到大枚举两段的分界点,将分界点左部分的区间删掉,保留右部分
求答案的时候暴力枚举左部分的区间,二分求multiset中的右边部分
void solve() {int n;cin >> n;vector<int> ve(n + 1), pre(n + 1);for (int i = 1; i <= n; ++i) {cin >> ve[i];pre[i] = pre[i - 1] + ve[i];}multiset<int> se;for (int i = 1; i <= n; ++i)for (int j = i; j <= n; ++j) se.insert(pre[j] - pre[i - 1]);int ans = LLONG_MAX;for (int j = 1; j <= n; ++j) {for(int i = j; i <= n; ++i) {se.erase(se.find(pre[i] - pre[j - 1]));}for (int i = j; i >= 1; --i) {int a = pre[j] - pre[i - 1];auto t = se.lower_bound(a);if (t != se.end()) ans = min(ans, *t - a);if (t != se.begin()) {t = prev(t);ans = min(ans, a - *t);}}}cout << ans;
}
2.18 天梯训练6

L2-2 天梯赛的赛场安排
思路:用优先队列维护要处理的学校,额外开个数组记录未满的房间,每次从前开始寻找即可
void solve() {int n, c;cin >> n >> c;vector<string> na(n);priority_queue<PII> q;for (int i = 0; i < n; ++i) {cin >> na[i];int x;cin >> x;q.push({x, i});}int ans = 0;vector<int> cnt(n);vector<int> add;while (q.size()) {auto [x, i] = q.top();q.pop();if (x >= c) {cnt[i] += x / c;ans += x / c;x %= c;if (x) q.push({x, i});} else {int t = -1;for (int j = 0; j < add.size(); ++j) {if (c - add[j] >= x) {t = j;break;}}if (t == -1) {ans ++, cnt[i] ++;add.push_back(x);} else add[t] += x, cnt[i] ++;}}for (int i = 0; i < n; ++i) cout << na[i] << ' ' << cnt[i] << '\n';cout << ans;
}L3-2 完美树
思路:dp
首先,若子树大小为偶数,黑白差值只能为0;若为奇数,黑白差值可以为1/-1,
因此可以设置状态为f[i][0/1/2]表示以i为根的子树,差值为-1/1/0的最小代价
考虑如何从以儿子为根的子树转移过来,首先子树大小为偶数的代价是确定的,这时候不确定的是子树大小为奇数的代价
要一半选差值为1的,一半选差值为-1的
这时候采用一个比较经典的做法,先都选取差值为1的,这时候要去除一半,需要维护所有儿子节点的f[i][0]-f[i][1],该值表示去除一个差值为1的情况,并且添加差值为-1的情况。排序后选最小的前半部分即为最小代价
void solve() {int n;cin >> n;vector<int> c(n + 1), p(n + 1);vector<vector<int> > ve(n + 1);for (int i = 1; i <= n; ++i) {cin >> c[i] >> p[i];int k;cin >> k;while (k --) {int v;cin >> v;ve[i].push_back(v);}}vector<vector<int> > f(n + 1, vector<int> (3));vector<int> cnt(n + 1);auto dfs = [&] (auto dfs, int u) -> void {cnt[u] = 1;if (c[u] == 1) f[u][1] = 0, f[u][0] = p[u];else f[u][0] = 0, f[u][1] = p[u];int s = 0;vector<int> g;for (auto v: ve[u]) {dfs(dfs, v);cnt[u] += cnt[v];if (cnt[v] % 2 == 0) s += f[v][2];else {s += f[v][0];g.push_back(f[v][1] - f[v][0]);}}if (c[u] == 1) g.push_back(-p[u]), s += p[u];else g.push_back(p[u]);std::sort(g.begin(), g.end());for (int i = 0; i < g.size() / 2; ++i) {s += g[i];}if (cnt[u] % 2 == 0) f[u][2] = s;else {f[u][0] = s;s += g[g.size() / 2];f[u][1] = s;}};dfs(dfs, 1);if (cnt[1] % 2 == 0) cout << f[1][2];else cout << min(f[1][0], f[1][1]);
}
L2-3 锦标赛
思路:
首先可以把比赛的晋级看成慢二叉树,根为赢家
此时一个节点败家分数一定是要大于等于两个儿子节点的败家分数的,可以根据该条件判断是否存在答案
接下来需要还原分数,每个节点的分数只会在以左儿子/右儿子为根的子树的叶子中出现,那么只要左子树/右子树满足上述条件就可以插入到左子树/右子树中,只需要插入一次即可,这时候可以暴力的枚举还未被插入的位置来进行插入
以下为节点对应的答案数组:
void solve() {int k;cin >> k;vector<int> ans(1 << k), ma(1 << k);for (int i = k - 1; i >= 0; --i) {for (int j = 0; j < 1 << i; ++j) {int x;cin >> x;int ok = 0;if (x >= ma[j << 1]) {for (int p = (j << 1) * (1 << k - i - 1); p < (j << 1 | 1) * (1 << k - i - 1); ++p) {if (!ans[p]) {ans[p] = x;ok = 1;break;}}}if (!ok && x >= ma[j << 1 | 1]) {for (int p = (j << 1 | 1) * (1 << k - i - 1); p < ((j + 1) << 1) * (1 << k - i - 1); ++p) {if (!ans[p]) {ans[p] = x;ok = 1;break;}}}if (!ok) {cout << "No Solution";return ;}ma[j] = max({x, ma[j << 1], ma[j << 1 | 1]});}}int x;cin >> x;if (x >= ma[0]) {for (int i = 0; i < 1 << k; ++i) {if (!ans[i]) ans[i] = x;cout << ans[i] << "\n "[i < (1 << k) - 1];}} else cout << "No Solution";
}2.19 蓝桥训练2
H-[蓝桥杯 2023 国 A] 相连的边
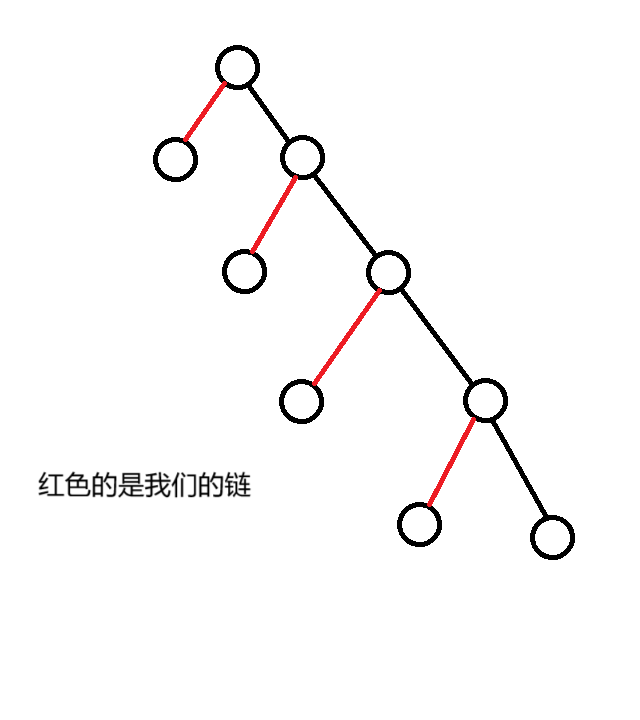
思路:有两种情况:菊花图和链,分别求这两种情况的个数
struct E {int u, v, d;
};
void solve() {int n;cin >> n;vector<vector<PII> > ve(n + 1);vector<E> g;for (int i = 2; i <= n; ++i) {int x, y;cin >> x >> y;ve[i].push_back({y, x});ve[x].push_back({y, i});g.push_back({i, x, y});}int ans = 0;for (int i = 1; i <= n; ++i) {std::sort(ve[i].begin(), ve[i].end(), greater<>());if (ve[i].size() >= 3) {int s = 0;for (int j = 0; j < 3; ++j) s += ve[i][j].first;ans = max(ans, s);}}for (int i = 0; i < n - 1; ++i) {auto [u, v, d] = g[i];if (ve[u].size() <= 1 || ve[v].size() <= 1) continue;d += ve[u][0].first + ve[v][0].first;if (ve[u][0].second == v) d += ve[u][1].first - ve[u][0].first;if (ve[v][0].second == u) d += ve[v][1].first - ve[v][0].first;ans = max(ans, d);}cout << ans;
}J-[蓝桥杯 2024 省 A] 零食采购
思路:最近公共祖先+差分
首先题目给的是一颗树,两点之间只有一条路径,且两点的最近公共祖先一定包含在这条路径中
并且给的种类个数只有20个,可以求出所有节点到根的路径中每种数出现的个数,那么便可以通过差分求出任何从根出发的路径中的任意两个节点之间每种数出现的个数,从而知道该数是否出现
再结合上最近公共祖先,从根开始跑,求出u和v的lca,另其为t,那么相当于求u→t、v→t的种类个数,u→t、v→t的种类个数就可以用差分来求
vector<int>g[N];//图
vector<int>dep(N);//深度
vector<vector<int>>f(N,vector<int>(20+5));//f[i][j]表示从i向祖先走2^j步vector<int> c(N);
vector<vector<int> > cnt(N, vector<int> (25));void dfs(int u){cnt[u][c[u]] ++;for(int i=0;i<g[u].size(); ++i){int to=g[u][i];if(dep[to])continue;f[to][0]=u;dep[to]= dep[u] + 1;for(int j=1;j<=20;++j) {f[to][j]=f[f[to][j-1]][j-1];cnt[to][j] = cnt[u][j];}dfs(to);}
}int lca(int a,int b){//求a和b的最近公共祖先if(dep[a]<dep[b])swap(a,b);for(int i=20;i>=0;--i)if(dep[f[a][i]]>=dep[b])a=f[a][i];if(a==b){//a走到breturn a;}//a和b到同一层后,一起向祖先走for(int i=20;i>=0;--i){if(f[a][i]!=f[b][i]){a=f[a][i],b=f[b][i];}}return f[a][0];
}void init(){dep[1]=1;//根为1dfs(1);
}
void solve() {int n, q;cin >> n >> q;for (int i = 1; i <= n; ++i) cin >> c[i];for (int i = 1; i < n; ++i) {int u, v;cin >> u >> v;g[u].push_back(v), g[v].push_back(u);}init();while (q --) {int u, v;cin >> u >> v;int ans = 0;int t = lca(u, v);for (int i = 1; i <= 20; ++i) {int s = cnt[u][i] + cnt[v][i] - 2 * cnt[t][i] + (c[t] == i);if (s) ans ++;}cout << ans << '\n';}}2.20 天梯训练7

7-10 多项式A除以B
思路:模拟
以上图片为多项式除法的过程,每次用多项式A的最高项与多项式B的最高项作比较,得出商多项式C
void solve() {int n, m;vector<double> a(N), b(N), c(N);cin >> n;int ma = 0, mb = 0;for (int i = 0; i < n; ++i) {int x;cin >> x >> a[x];ma = max(ma, x);}cin >> m;for (int i = 0; i < m; ++i) {int x;cin >> x >> b[x];mb = max(mb, x);}while (ma >= mb) {int ed = ma - mb;double cd = a[ma] / b[mb];c[ed] += cd;for (int i = mb; i >= 0; --i) {a[i + ed] -= b[i] * cd;}while (ma >= 0 && fabs(a[ma]) < eps) ma --;}auto prt = [=](vector<double> x) {vector<PDD> ans;for (int i = N - 1; i >= 0; --i) {if (fabs(x[i]) > eps) ans.push_back({i, x[i]});}if (ans.empty()) cout << "0 0 0.0\n";else {cout << ans.size();for (int i = 0; i < ans.size(); ++i) {cout << ' ' << (int)ans[i].first << ' ';cout << fixed << setprecision(1) << ans[i].second;}cout << '\n';}};prt(c);prt(a);
}7-15 球队“食物链”
思路:dfs+剪枝
这道题首先要注意[i][j]=L也代表j赢了i
答案是全排列,并且是关系构成了环,说明环上任意排列都是合法的,那么最小排列一定是1开始的
还需要考虑剪枝,已经知道是从1开始的,说明dfs到当前数时,剩下还未被用到的数中,一定存在一个数能赢1,否则当前的排列就不合法,无需再搜索下去
void solve() {int n;cin >> n;vector<string> ve(n + 1);for (int i = 1; i <= n; ++i) {cin >> ve[i];ve[i] = " " + ve[i];}vector<int> ans, st(n + 1);auto dfs = [&](auto dfs, int u) ->void {if (ans.size() == n) {cout << ans[0];for (int i = 1; i < n; ++i) cout << ' ' << ans[i];::exit(0);}bool ok = 0;for (int i = 1; i <= n; ++i) {if (!st[i] && (ve[i][1] == 'W' || ve[1][i] == 'L')) {ok = true;break;}}if (!ok) return ;for (int i = 1; i <= n; ++i) {if (st[i] || !(ve[u][i] == 'W' || ve[i][u] == 'L')) continue;st[i] = 1;ans.push_back(i);dfs(dfs, i);st[i] = 0;ans.pop_back();}};ans.push_back(1);st[1] = 1;dfs(dfs, 1);cout << "No Solution";
}2.21 蓝桥训练3

C-[蓝桥杯 2023 省 A] 平方差
思路:首先打表可以发现,缺少了4k+2(k≥0),直接减去区间缺少的部分
证明:s=x2-y2=(x+y)(x-y),当x+y为奇数时s一定为奇数,当x+y为偶数时s一定为4的倍数,剩下的部分即为4k+2(k≥0)
void solve() {int l, r;cin >> l >> r;int ans = (r + 2) / 4 - (l + 1) / 4;ans = r - l + 1 - ans;cout << ans;
}D-[蓝桥杯 2024 省 C] 数字诗意
思路:
首先知道等差数列的区间和为s=(n + m)(n - m + 1)/2,并且(n + m)与(n - m + 1)的奇偶性不同
说明s一定包含奇数因子,那么不可能存在的数为2k
void solve() {int n;cin >> n;int ans = 0;for (int i = 1; i <= n; ++i) {int x;cin >> x;int p = log2(x);if ((1ll << p) == x) ans ++;}cout << ans;
}E-[蓝桥杯 2019 国 B] 解谜游戏
思路:
模拟下操作1的过程,发现下图中编号相同的一定能进行操作3,且每种编号刚好外中内圈为3、2、1个
说明每种编号的绿、红、黄的颜色刚好要有3、2、1个才能满足条件
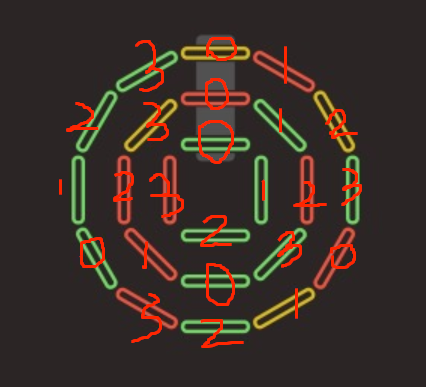
void solve() {string a, b, c;cin >> a >> b >> c;for (int i = 0; i < 4; ++i) {vector<int> cnt(100);cnt[a[i]]++, cnt[b[i]]++, cnt[c[i]]++;cnt[a[i + 4]]++, cnt[a[i + 8]] ++, cnt[b[i + 4]]++;if (cnt['G'] != 3 || cnt['R'] != 2 || cnt['Y'] != 1) {cout << "NO\n";return ;}}cout << "YES\n";
}H-[蓝桥杯 2024 国 A] 最长子段
思路:
首先可以将式子转化成acL - ∑si(1≤i<L)> abR - ∑si(1≤i≤R)
另Ai=acL - ∑si(1≤i<L),Bi=abR - ∑si(1≤i≤R),此时将A、B都按降序排序
若满足Ai>Bj,说明(i,j)为一个答案,同时(i,j+1)、(i,j+2)....也都满足条件
此时记录B的后缀编号最大值suf[i],对于满足条件的Ai>Bj,O(1)便可查出B的最大的编号
void solve() {int n, a, b, c;cin >> n >> a >> b >> c;vector<int> s(n + 5);for (int i = 1; i <= n; ++i) cin >> s[i], s[i] += s[i - 1];vector<PII> A(n + 1), B(n + 1);for (int i = 1; i <= n; ++i) {A[i].first = a * c * i - s[i - 1];B[i].first = a * b * i - s[i];A[i].second = B[i].second = i;}std::sort(A.begin() + 1, A.end(), greater<PII>());std::sort(B.begin() + 1, B.end(), greater<PII>());for (int i = n - 1; i >= 1; --i) {B[i].second = max(B[i].second, B[i + 1].second);}int ans = 0, idx = 1;for (int i = 1; i <= n && idx <= n; ++i) {while (idx <= n && B[idx].first >= A[i].first) idx ++;if (idx > n) break;ans = max(ans, B[idx].second - A[i].second + 1);}cout << ans;
}K-[蓝桥杯 2023 省 A] 买瓜
思路:
首先考虑暴搜,时间复杂度为3n=330
考虑折半搜索,时间可以为3n/2,用unordermap存前半部分的所有值的最少次数
再加上剪枝优化,当前次数已经大于已有答案,当前值已经超过m,这些情况都可以减去
为了方便统计,将所有值都乘上2,m值同样
unordered_map<int, int> st;
void solve() {int n, m;cin >> n >> m;m *= 2;vector<int> a(n + 1);for (int i = 1; i <= n; ++i) cin >> a[i], a[i] *= 2;int ans = INT32_MAX;std::sort(a.begin() + 1, a.end());int nn = n >> 1;auto dfs1 = [&](auto dfs1, int u, int sum, int cnt) ->void {if (cnt > ans || sum > m) return ;if (sum == m) {ans = min(ans, cnt);return ;}if (u >= nn) {if (st.count(sum)) st[sum] = min(st[sum], cnt);else st[sum] = cnt;return ;}dfs1(dfs1, u + 1, sum + a[u + 1], cnt);dfs1(dfs1, u + 1, sum, cnt);dfs1(dfs1, u + 1, sum + a[u + 1] / 2, cnt + 1);};auto dfs2 = [&](auto dfs2, int u, int sum, int cnt) -> void {if (sum > m || cnt > ans) return ;if (sum == m) {ans = min(ans, cnt);return ;}if (u >= n) {if (st.count(m - sum)) ans = min(ans, cnt + st[m - sum]);return ;}dfs2(dfs2, u + 1, sum + a[u + 1], cnt);dfs2(dfs2, u + 1, sum, cnt);dfs2(dfs2, u + 1, sum + a[u + 1] / 2, cnt + 1);};dfs1(dfs1, 0, 0, 0);dfs2(dfs2, nn, 0, 0);if (ans == INT32_MAX) cout << -1;else cout << ans;
}
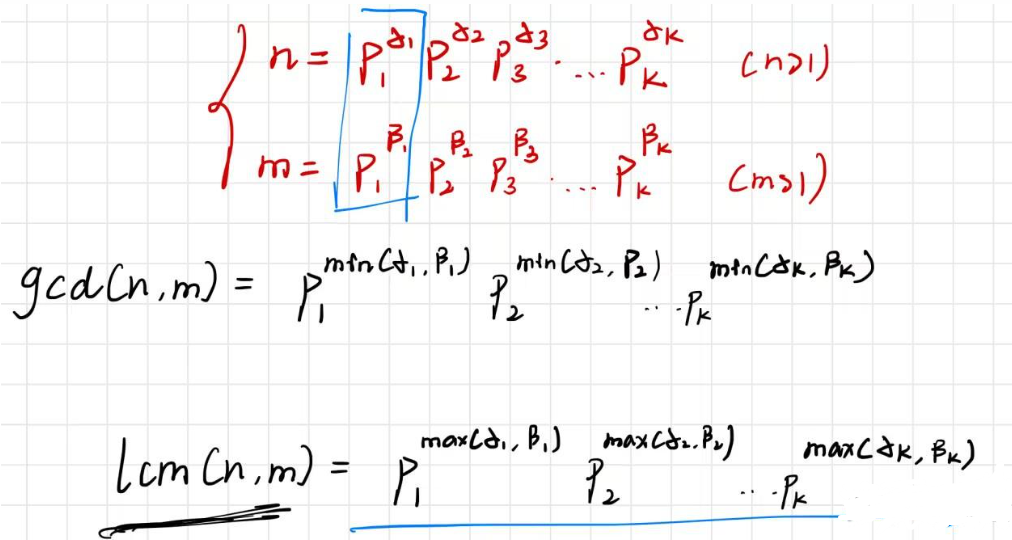
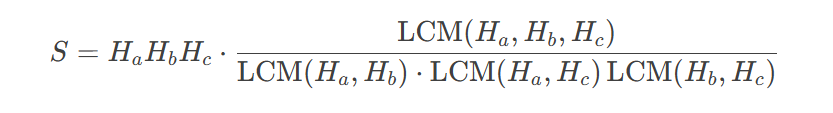

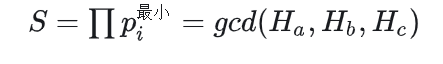


![双向广搜 P1032 洛谷 [NOIP 2002 提高组] 字串变换](https://img2024.cnblogs.com/blog/3600051/202502/3600051-20250223190106347-861659747.png)