容斥、反演、卷积与高维前缀和

news/2025/2/28 16:20:33/文章来源:https://www.cnblogs.com/haozexu/p/18743497

数学的大网磅礴地展开了。

容斥、反演、卷积与高维前缀和 Stream

Draft

我觉得，我们最开始使用的时候，肯定是从最普通基础的容斥原理讲起的，因为这就是我们实际遇到的一种问题：

问题 1 通过集合交求集合并

假设班里有 $10$ 个学生喜欢数学，$15$ 个学生喜欢语文，$21$ 个学生喜欢编程，班里至少喜欢一门学科的有多少个学生呢？

我们小学的时候就学习过这种问题，当时，我们会画 Venn 图来解决：

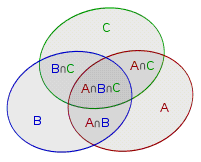
$容斥原理 - venn 图示例$

我们将这个形式一般化，就变成了：

公式 1 容斥原理

\[\left|\bigcup_{i=1}^{n}S_i\right|=\sum_{m=1}^n(-1)^{m-1}\sum_{a_i<a_{i+1} }\left|\bigcap_{i=1}^mS_{a_i}\right| \]

这个形式很有意思，它为什么正确？

定理 1 二项式定理

\[(x+y)^n=\sum_{k=0}^n{n\choose k}x^{n-k}y^k \]

证明容斥原理

一个元素一个元素考虑，我们需要算出最后的并集，所以每一个元素的贡献都应该是 $1$，我们假设元素 $x$ 在 $S_1,S_2,\dots,S_m$ 这些集合中，那么他的贡献次数就是：在一个集合中-在两个集合的交中+在三个集合的交中……

那么贡献就分别是：${m\choose 1},{m\choose 2},\dots,{m\choose m}$，总和就是

\[\sum_{i=1}^m (-1)^{i-1}{m\choose i}={m\choose 0}-\sum_{i=0}^m (-1)^i{m\choose i} \]

这个好像就是二项式定理的形式！那么他的总和就是 $1$。$\square$

所以证明它的关键想法是，我们要计算每个元素贡献，确保为 $1$。

我们通过容斥原理，将求集合并转化为求集合交。这一切是通过附加一个系数实现的。

To do:从线性代数的角度说明。

但是，当问题比较复杂的时候，容斥原理可能就似了。

问题 2 错位排列计数

对于一个长为 $n$ 的排列 $p$，称数 $i$ 在初始位置当且仅当 $p_i=i$，现在要求有多少序列满足恰好有 $m$ 个元素在初始位置。

这个问题不好直接计算，但是我们马上就指出，可以用钦定 $k$ 个元素保持原位的方案数来计算原问题的答案。我们设原问题规模为 $k$ 的实例的答案是 $f(k)$，转化后问题的答案是 $g(k)$

那么，

\[g(k)={n\choose k}(n-k)! \]

现在如何将它转化为 $f(k)$ 呢？我们还是考虑一个方案的贡献要为 $1$。

我们考虑一个恰好有 $m$ 个元素在初始位置的方案，它在 $g(m)$ 中会被计算一次。但是，$g(m)$ 中还包含实际上有多于 $m$ 个元素在初始位置的方案，那么我们尝试减去 $g(m+1)$。我们现在看看我们是否使得重复的元素都恰好被减去一次，对于一个有 $m+1$ 个元素在初始位置的方案，我们发现在 $g(m)$ 中，有 ${m+1\choose m}$ 种钦定方案都计算了它，所以它被计算了不止一次，在 $g(m+1)$ 时它只被减去一次，减少了，应该减去 ${m+1\choose m}$ 次。

好的，我们减去 ${m+1\choose m}g(m+1)$，然后我们不妨再考虑下有 $m+2$ 个元素在初始位置的方案，它在 $g(m)$ 中计算了 ${m+2\choose m}$ 次，在 $g(m+1)$ 中计算了 ${m+2\choose m+1}$ 次，被减掉了 ${m+2\choose m+1}{m+1\choose m}=(m+2)^{\underline 2}$ 次，又减多了。以此类推，在 $g(m+2)$ 中被算一次，此时再补上 ${m+2\choose m}$ 就正好对答案不造成贡献了。

我们写出来发现的规律：

\[f(m)=\sum_{k=m}^n(-1)^{k-m}{k\choose m}g(k) \]

上面的推导过程其实蕴含着下面这条性质：

\[g(m)=\sum_{k=m}^n{k\choose m}f(k) \]

好的，我们实际上得到了这样的等价关系：