微积分的本质——导数.18790288

本篇为3b1b系列【微积分的本质】笔记
原视频：02-导数的悖论 | 03-用几何来求导 | 04-直观理解链式法则和乘积法则

定义导数

这是一个随着时间变化，车辆行驶距离的坐标图

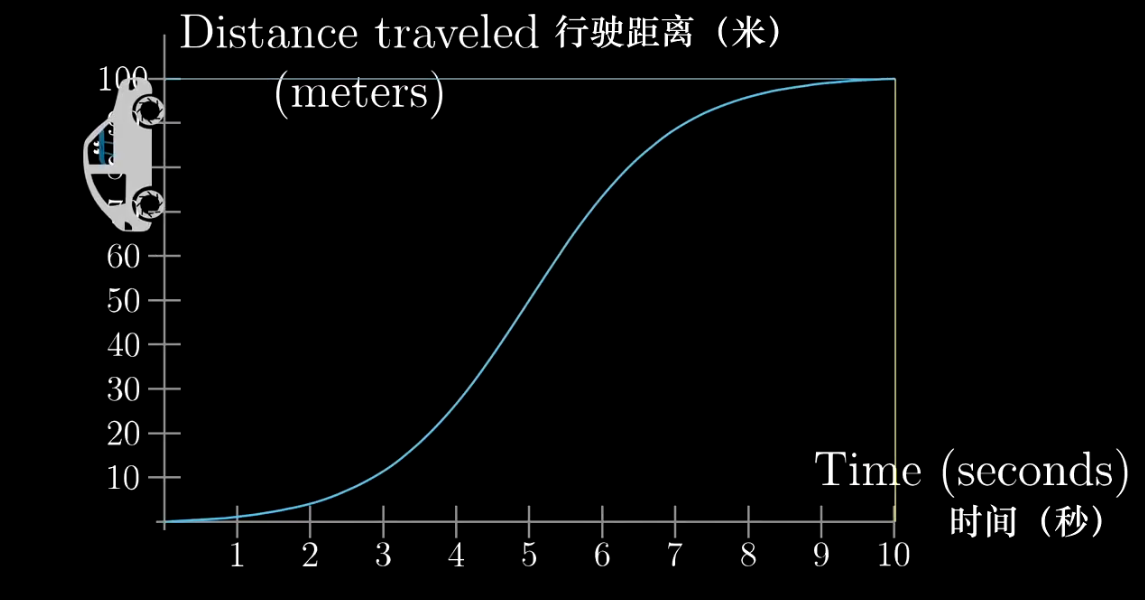
在横轴的任何一个点\(t\)上，如果你去查看车的车速表，上面都有一个数字表示当前的车速，但这是如何计算的？因为要知道，若\(t\)被固定在一个瞬间，车速必然是0，因为此时车是静止的。

所以，瞬时的车速是不存在的。

一旦要谈论速度，必然不能让\(t\)固定。现实中车速表的做法是，让\(t\)有一个极短时间的变化\(dt\)（假如0.0001秒），再采集\(t\)到\(dt\)时间段内行驶的距离（假设是\(ds\)），用\(\frac{ds}{dt}\)即可得到一个短时间内的速度。如果不考虑物理限制，\(dt\)越趋近于\(0\)，我们得到的车速越精确。同时，\(\frac{ds}{dt}\)也是过速度曲线上时间变化前后两点的切线斜率。

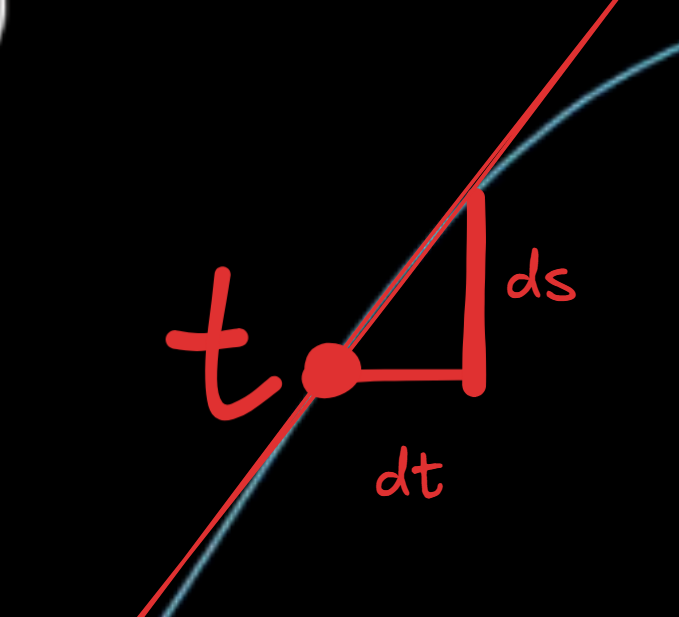
设上图中车随时间行驶的距离的函数为\(s(t)\)

在实践中我们可以给出一个关于\(t\)的函数来计算车速：\(\frac{ds}{dt}(t)=\frac{s(dt+t) - s(dt)}{dt}\)，对于算法来说，下一步就是选定一个合理的\(dt\)。

对于数学来说，研究特定的\(dt\)没有意义，如果带入极限思想，让\(dt\)无限趋近于0，我们可以得出一个计算瞬时车速最好的函数，对于给定\(t\)，该函数的结果无限趋近于\(t\)点在函数\(s(t)\)上切线的斜率，这就是导数。

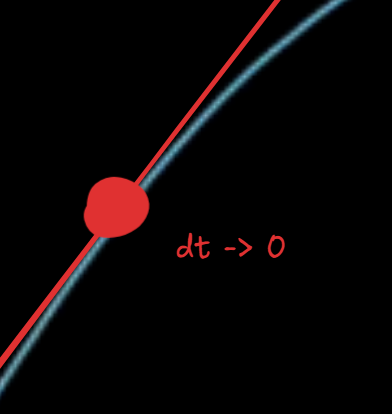
或者可以说：对于函数\(f\)以及给定点\(x\)，导数是\(f\)上\(x\)附近变化率的最佳近似，等于在\(f\)上\(x\)点切线的斜率。

在下图的现实意义上，它反映了车速的变化率：

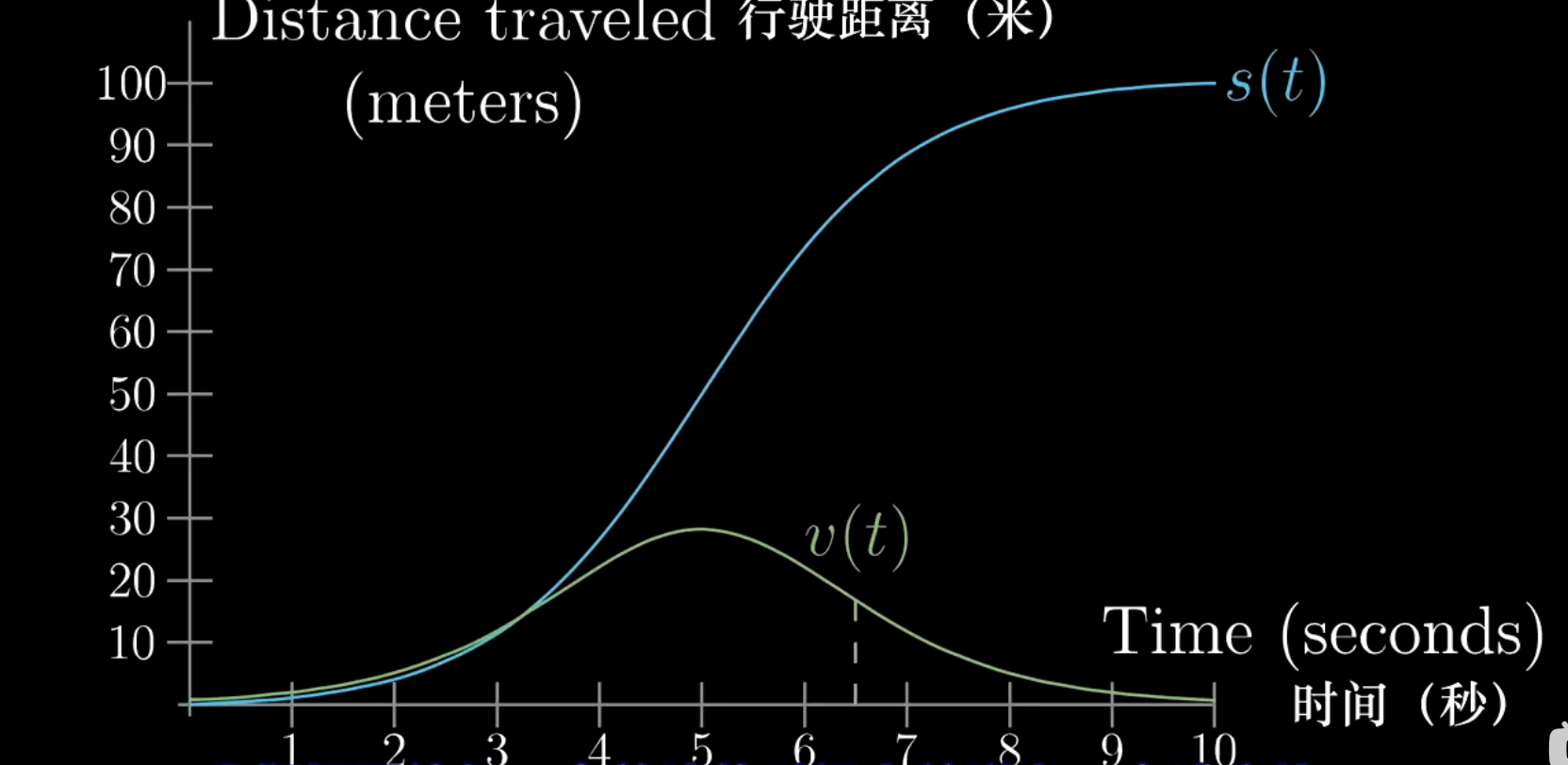
刚刚我们用了符号\(dt\)表示了自变量车速\(t\)的微小变化，\(ds\)表示了因变量或函数结果\(s(t)\)因为车速微小变化\(dt\)产生的变化，最后，使用\(\frac{ds}{dt}(t)\)来表示计算车速的实际函数。而在数学中，这就是导数的一种书写形式，我们把\(f(x)\)的导数写作\(\frac{df(x)}{dx}\)、\(\frac{dy}{dx}\)或直接写作\(f'(x)\)、\(y'\)。

用几何看待导数

\(f(x)=x^2\)

如下图，当\(x\)产生微小变化\(dx\)时，图中正方形的面积的微小变化\(df\)多了\(2xdx+dx^2\)，当\(dx\)无限趋近于零，后面的\(dx^2\)可以省略，则\(df=2xdx, \frac{df}{dx}=2x\)。

注意，\(df\)是随着\(x\)产生微小变化后，函数值（面积）的变化，而\(\frac{df}{dx}\)则是一个关于\(x\)的函数，产生\(f(x)=x^2\)这个函数上任意点\(x_i\)的导数（面积的变化率）。后面我们不会再重复。

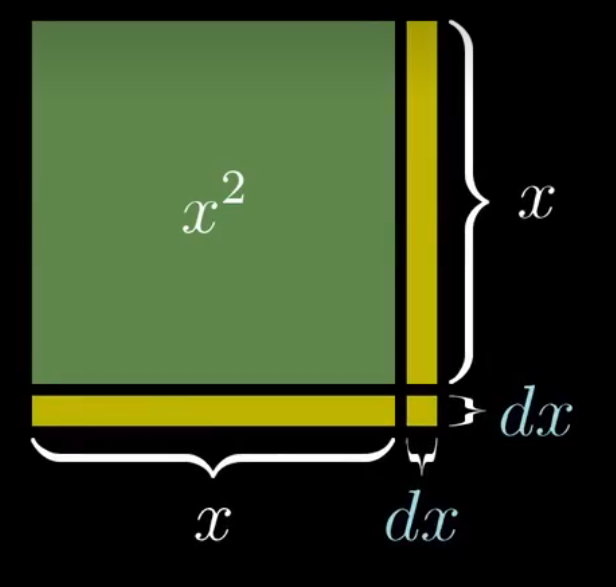
\(f(x)=x^n, f'(x)=nx^{n-1}\)

加法法则：\(f(x) + g(x)\)

下图展示了一个两个函数相加的例子，我们假设两函数相加产生的新函数是\(h(x)\)，当\(x\)产生微小变化，\(dh(x)=df(x)+dg(x)=cos(x)dx + 2xdx, \frac{dh}{dx}=cos(x) + 2x\)

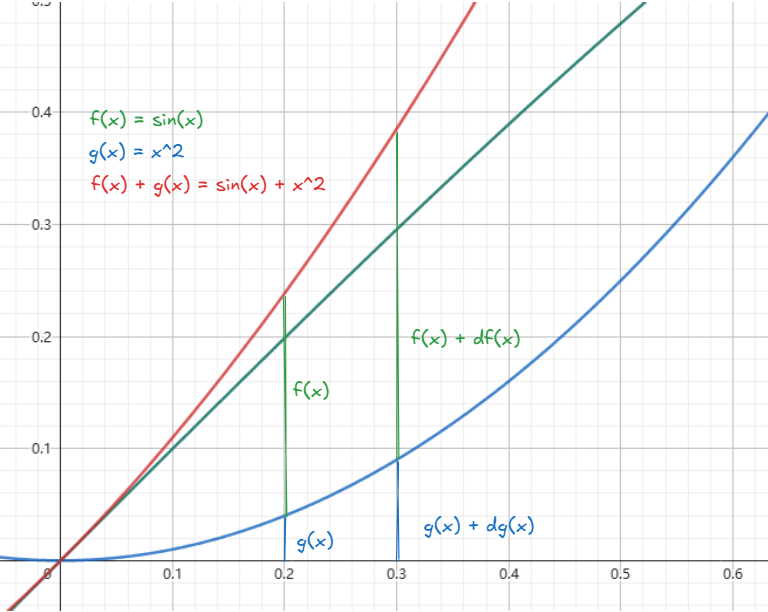
\(h(x)=f(x)+g(x), h'(x)= f'(x) + g'(x)\)

乘法法则：\(f(x)\times g(x)\)

对于乘积，以面积来可视化最好。

如下图，四边形的横边是\(f(x)=sin(x)\)，纵边是\(g(x)=x^2\)，面积是复合函数\(h(x)=f(x)g(x)\)。

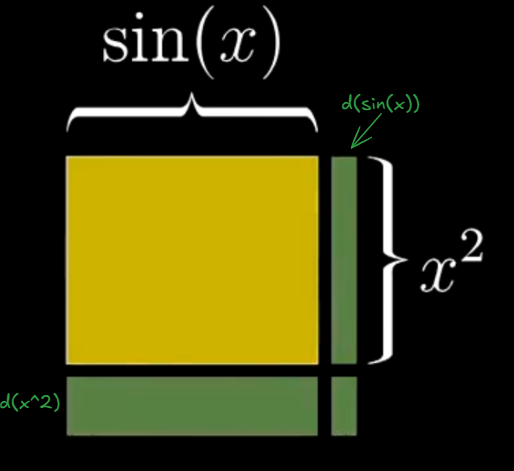
当\(x\)发生微小变化，\(dh=sin(x)d(x^2)+x^2d(sin(x))+d(x^2)d(sin(x))=sin(x)2xdx+x^2cos(x)dx, \frac{dh}{dx}=sin(x)2x+x^2cos(x)\)

\(h(x)=f(x)g(x), h'(x)= f'(x)g(x) + f(x)g'(x)\)

链式法则：\(f(g(x))\)

几何展示略

\(h(x)=f(g(x)), h'(x)=f'(g(x))g'(x)\)