上下界网络流
上下界流就是在普通的网络中加了下界。却还是要对于非源汇点,满足入流=出流,于是可能存在不合法的情况。
基础款
无源汇可行流
就是:
-
对于每个点,入流 = 出流
-
对于每条边,流量 $\in $ 合法区间
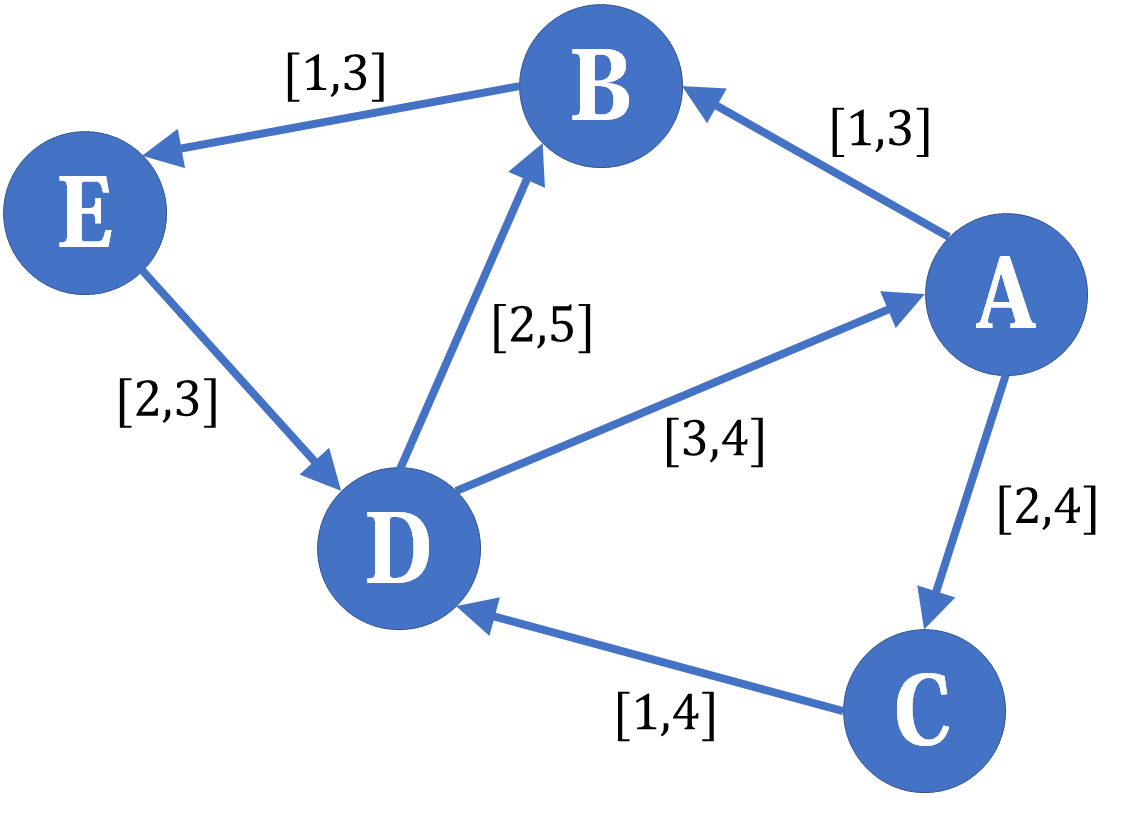
我们先满足其下界,但这样可能出现入流 \(\ne\) 出流的情况,于是在差网络上调整。
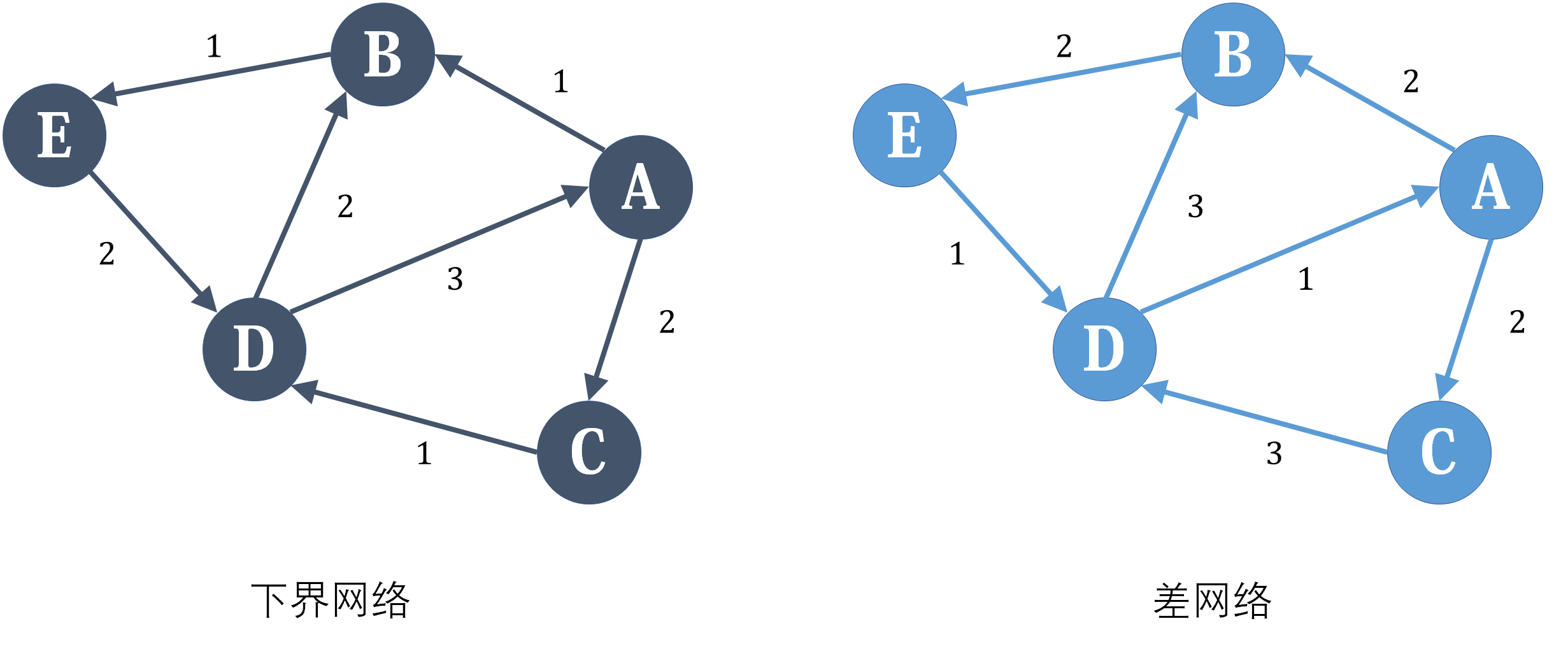
在强制满足下届后,对于一个点 \(x\),设其入流总和为 \(in\),出流总和为 \(out\) 可能有三种情况:
-
\(in=out\):这是好的,不用在处理了。
-
\(in<out\):即在差网络上需要额外的入流,可以将 \(x\) 与人造汇点 \(T'\) 相连,边权为 \(out-in\),这样当 \(x\) 在差网络上流量平衡时,就恰好满足了额外流入。
-
\(in>out\):即在差网络上需要额外的出流,同理将人造源点 \(S'\) 与 \(x\) 相连,边权为 \(in-out\),即可。
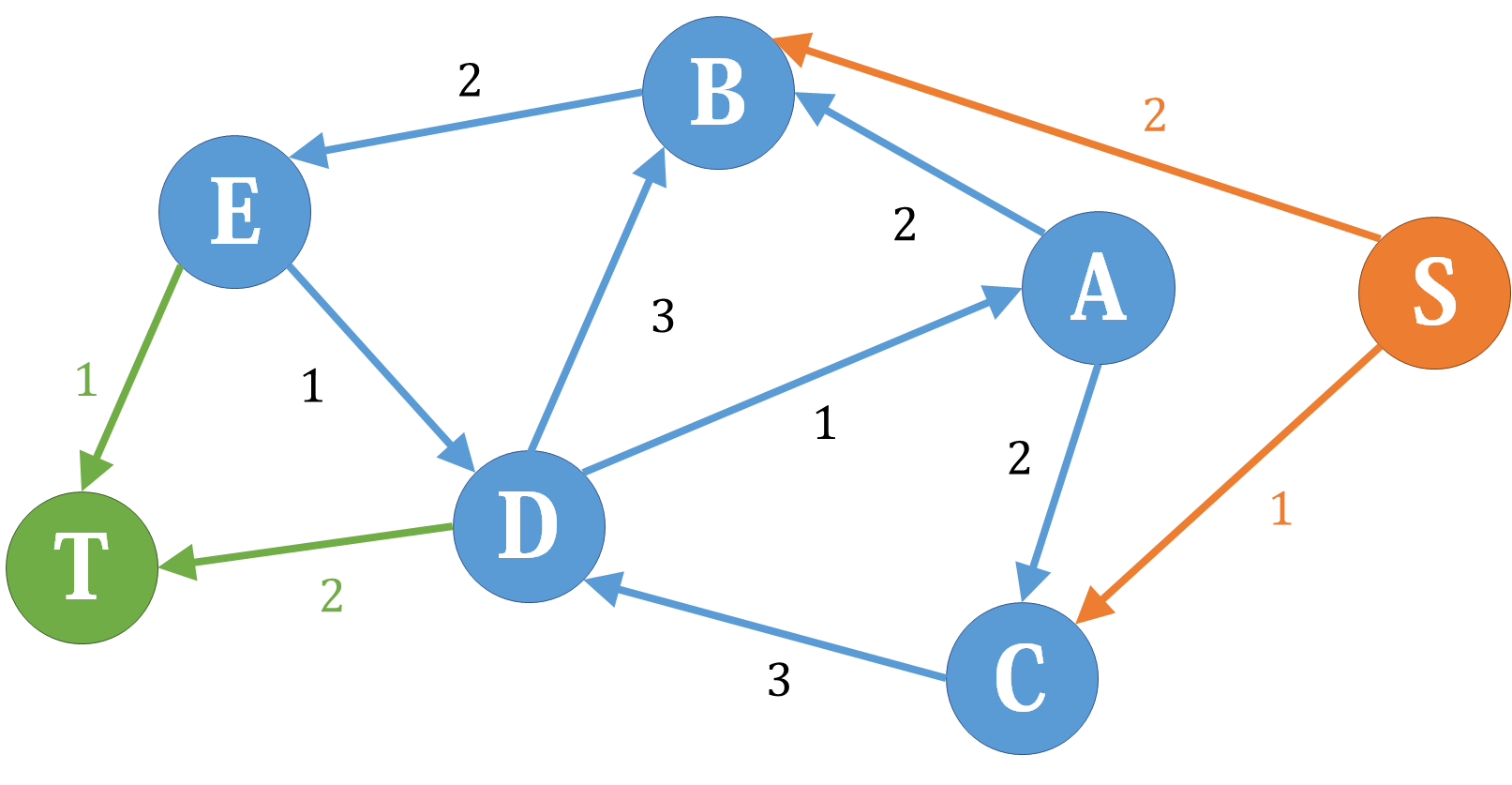
建好后跑 \(S'\to T'\) 的最大流,使得所有与 \(S',T'\) 相连的边都满流即可。
如果 \(S',T'\) 存在未满流的边,则不存在。
综上我们可以得到若干性质:
-
一个网络存在可行流要求这个网络必须强连通。
-
\(a\to b\) 的流 = \(b\to a\) 的流
有源汇可行流
就是可以存在一个源点 \(S\) 与汇点 \(T\) 不满足流量守恒定律。
因为 \(S\) 只能出, \(T\) 只能进,连一条 \(T\to S\) 边权为 \([0,+\infin)\) 的边即可转化为无源汇的情况,这条边的流量即为 \(S\to T\) 的流量。
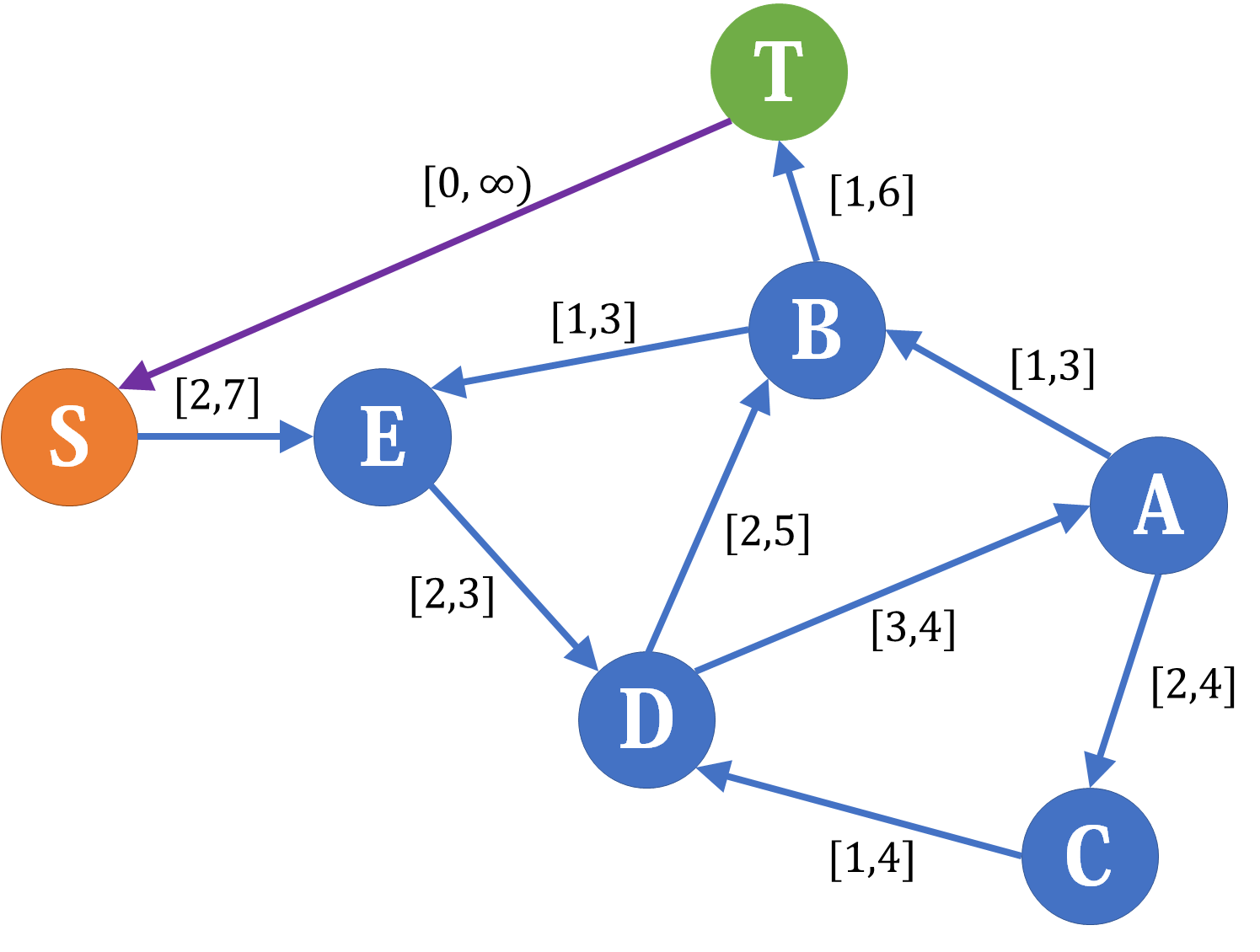
提高款
有源汇最大流
即 \(S\to T\) 满足条件的最大流量。
由于最大流增广路的选择是不可控的,最后差网络(不包括人造源汇点)的流量是不可控的也就不能保证差网络的其中两点的流量是最大的。
于是,我们在参量差网络上跑 \(S\to T\) 的最大流即可,这是因为最大流的每次增广不影响网络的流量平衡关系(即对于每个点 \(x\),不影响 \(in_x-out_x\) 的值,这是因为每次增广都是进 \(x\) 多少流量,出多少流量,除了 \(S,T\) 这两个点)。
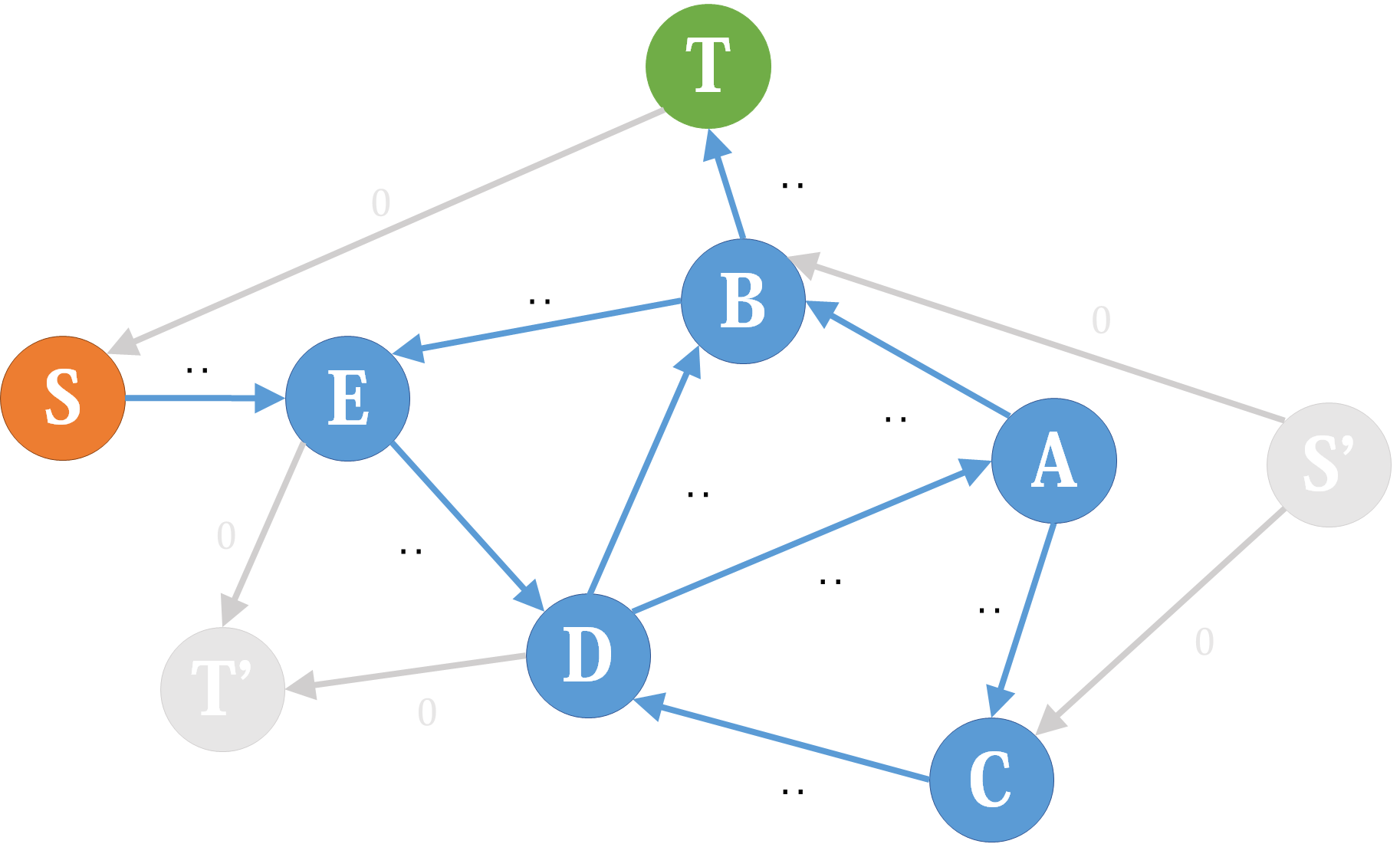
答案就是原来 \(S\to T\) 的流量加上这个最大流。
这种方法适用于网络中任何两个点作为 \(S,T\),但是要注意 \(S,T\) 本身不满足流量平衡定律。
有源汇最小流
即 \(S\to T\) 满足条件的最大流量。
同理跑 \(T\to S\) 的最大流即可,答案就是原来 \(S\to T\) 的流量减去这个最大流。
可以发现 \(S\to T\) 满足条件的可行流的流量是一个区间,最小流与最大流就是其左右端点。
最小费用可行流
下界网络满流的费用,加上在差网络上跑MCMF后得到的费用之和。有没有源汇都可以。
消去负权边
在求最小费用可行流的时候,可能会出现负环导致亖掉,注意到将原网络分离出的”下界网络“不一定全部选用”下届“,加入有负权边 \((a,b)\),在”下界网络“中强制使其满流,然后加入其反边,这个反边权值一定为正,于是就消去了所有负权边。
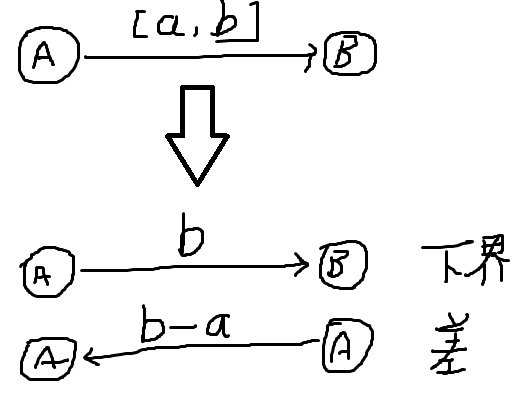
在处理一般网络流问题时也可以使用这个方法。
进阶款
最小费用最大流
先跑出最小费用可行流,在跑出 \(S\to T\) 的最小费用最大流,答案为其和。