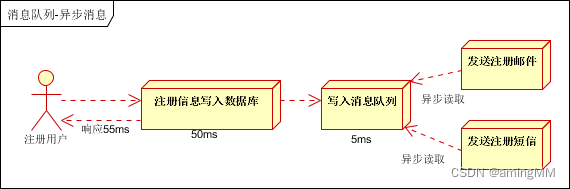
定理6.3.2
如果n是对于基b的强伪素数，则n是对于基b得到欧拉伪素数

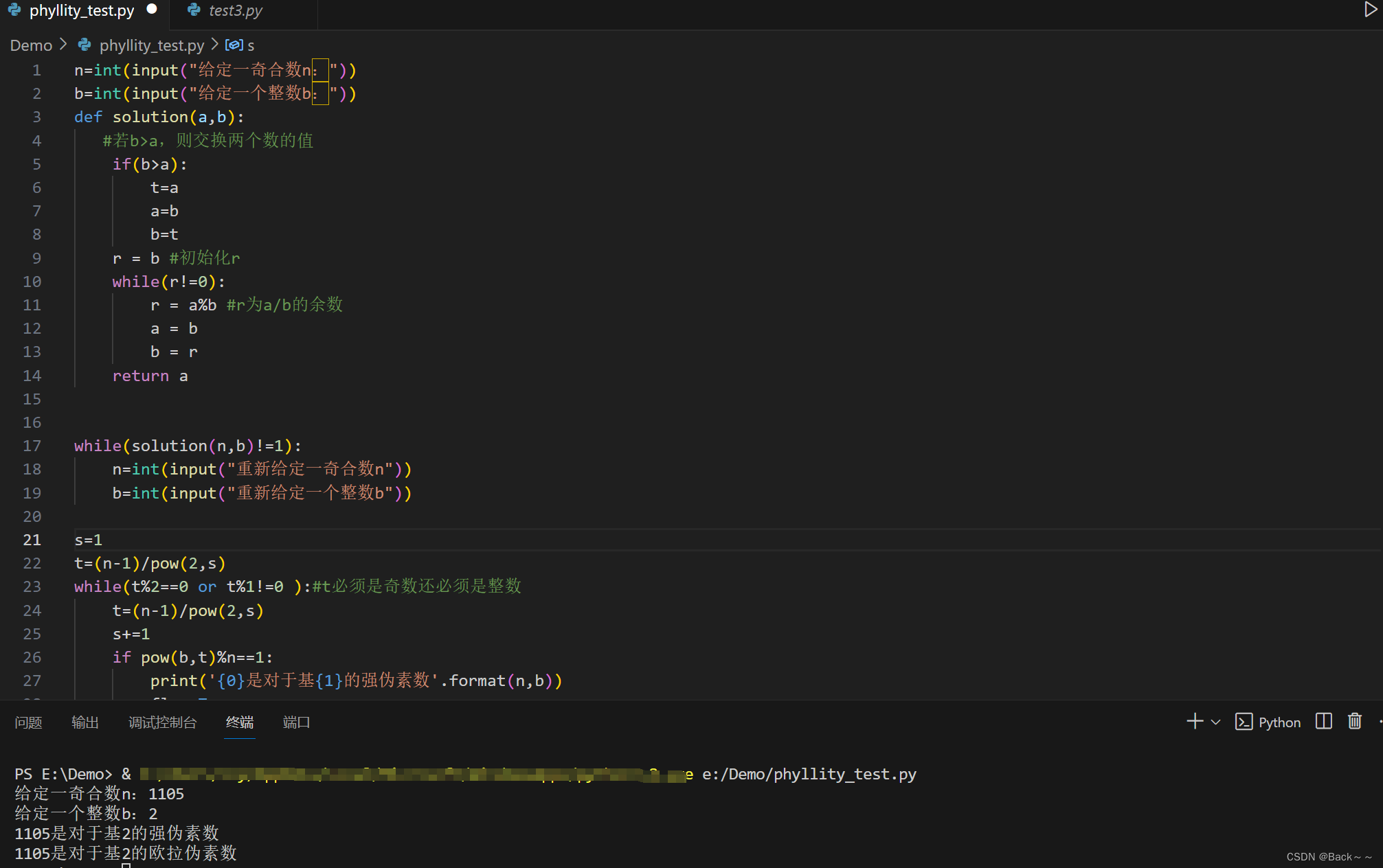
n=int(input("给定一奇合数n："))
b=int(input("给定一个整数b："))
def solution(a,b):#若b>a，则交换两个数的值if(b>a):t=aa=bb=tr = b #初始化rwhile(r!=0):r = a%b #r为a/b的余数a = bb = rreturn a  while(solution(n,b)!=1):n=int(input("重新给定一奇合数n"))b=int(input("重新给定一个整数b"))flag=False
s=1
t=(n-1)/pow(2,s)
if pow(b,t)%n==1:print('{0}是对于基{1}的强伪素数'.format(n,b))flag=True
else:while(t%2==0 or t%1!=0 ):#t必须是奇数还必须是整数t=(n-1)/pow(2,s)s+=1if pow(b,t)%n==1:print('{0}是对于基{1}的强伪素数'.format(n,b))flag=True##判断欧拉伪素数
if flag==True:q=(n-1)/2f=((n**2)-1)/8if pow(b,q)%n==1 and pow(-1,f)==1:print('{0}是对于基{1}的欧拉伪素数'.format(n,b))

定理6.3.2
设一个奇合数，则n是对于基b的强伪素数的可能性至多为25%

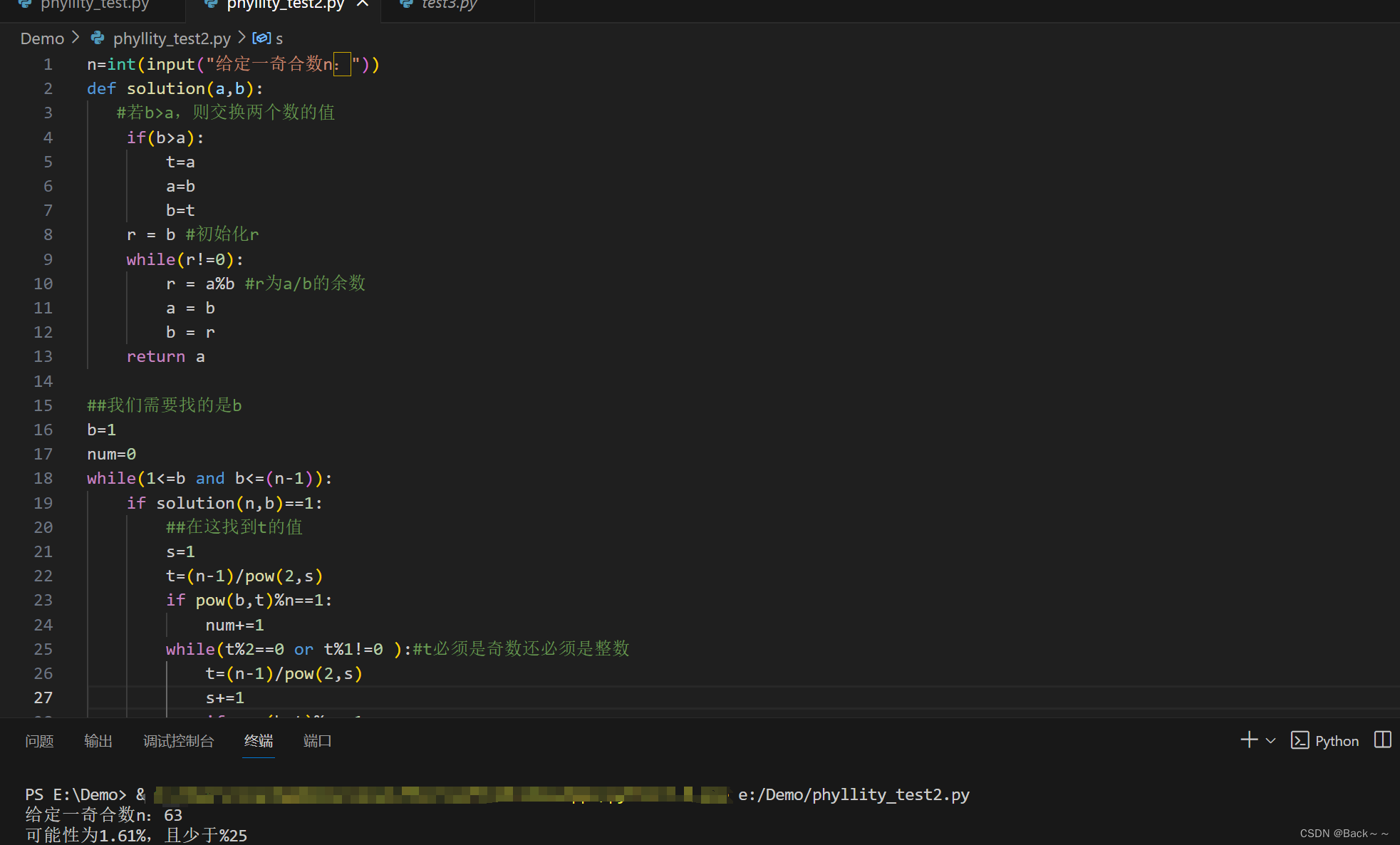
n=int(input("给定一奇合数n："))
def solution(a,b):#若b>a，则交换两个数的值if(b>a):t=aa=bb=tr = b #初始化rwhile(r!=0):r = a%b #r为a/b的余数a = bb = rreturn a  ##我们需要找的是b
b=1
num=0
while(1<=b and b<=(n-1)):if solution(n,b)==1:##在这找到t的值s=1t=(n-1)/pow(2,s)if pow(b,t)%n==1:num+=1while(t%2==0 or t%1!=0 ):#t必须是奇数还必须是整数t=(n-1)/pow(2,s)s+=1if pow(b,t)%n==1:num+=1b+=1propertion=(num/(n-1))*100
if propertion<=25:print('可能性为{:.2f}%，且少于%25'.format(propertion))