第七章 回溯算法part06

1.LeetCode.重新安排行程

先跳过

1.1题目链接：

文章讲解：代码随想录

1.2思路：

1.3附加代码如下所示：

2.LeetCode. N皇后

2.1题目链接：

文章讲解：代码随想录
视频讲解：

2.2思路：都知道n皇后问题是回溯算法解决的经典问题，但是用回溯解决多了组合、切割、子集、排列问题之后，遇到这种二维矩阵还会有点不知所措。

首先来看一下皇后们的约束条件：

不能同行
不能同列
不能同斜线
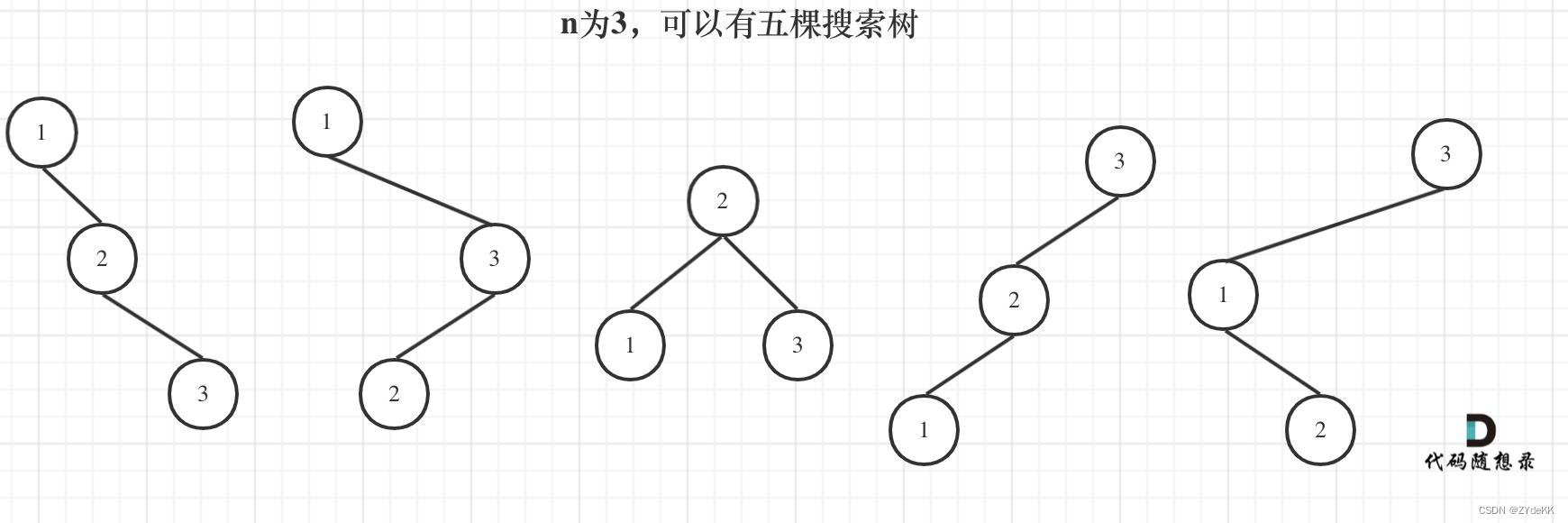
确定完约束条件，来看看究竟要怎么去搜索皇后们的位置，其实搜索皇后的位置，可以抽象为一棵树。
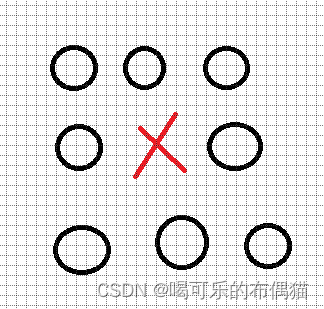
下面我用一个 3 * 3 的棋盘，将搜索过程抽象为一棵树，如图：

2.3附加代码如下所示：

class Solution {
public:vector<vector<string>>result;// n 为输入的棋盘大小// row 是当前递归到棋盘的第几行了void backtracking(int n,int row,vector<string>&chessboard){if(row==n){result.push_back(chessboard);return;}for(int col=0;col<n;col++){if(isValid(row,col,chessboard,n))// 验证合法就可以放{chessboard[row][col]='Q';// 放置皇后backtracking(n,row+1,chessboard);chessboard[row][col]='.';//回溯，撤销皇后}}}bool isValid(int row,int col,vector<string>&chessboard,int n){//检查列for(int i=0;i<row;i++){if(chessboard[i][col]=='Q'){return false;}}//检查45度是否存在皇后for(int i=row-1,j=col-1;i>=0&&j>=0;i--,j--){if(chessboard[i][j]=='Q'){return false;}}//检查135度是否存在皇后for (int i=row-1,j=col+1;i>=0&&j<=n;i--,j++){if(chessboard[i][j]=='Q'){return false;}}return true;}vector<vector<string>> solveNQueens(int n) {result.clear();//vector<string>chessboard(n,string(n,'.'));std::vector<std::string> chessboard(n, std::string(n, '.'));//这是使用标准库函数中的vectorbacktracking(n,0,chessboard);return result;}
};

3.LeetCode.解数独

3.1题目链接：

文章讲解：代码随想录
视频讲解：

3.2思路：N皇后问题是因为每一行每一列只放一个皇后，只需要一层for循环遍历一行，递归来遍历列，然后一行一列确定皇后的唯一位置。本题就不一样了，本题中棋盘的每一个位置都要放一个数字（而N皇后是一行只放一个皇后），并检查数字是否合法，解数独的树形结构要比N皇后更宽更深。

3.3附加代码如下所示：

class Solution {
public:bool backtracking(vector<vector<char>>&board){for(int i=0;i<board.size();i++) // 遍历行{for(int j=0;j<board[0].size();j++) // 遍历列{if(board[i][j]=='.'){for(char k='1';k<='9';k++)// (i, j) 这个位置放k是否合适{if(isValid(i,j,k,board)){board[i][j]=k; // 放置kif(backtracking(board))return true;// 如果找到合适一组立刻返回board[i][j]='.'; // 回溯，撤销k}}return false; // 9个数都试完了，都不行，那么就返回false}}}return true;}bool isValid(int row,int col,char val,vector<vector<char>>&board){for(int i=0;i<9;i++){if(board[row][i]==val){return false;}}for(int j=0;j<9;j++){if(board[j][col]==val){return false;}}int startrow=(row/3)*3;int startcol=(col/3)*3;for(int i=startrow;i<startrow+3;i++){for(int j=startcol;j<startcol+3;j++){if(board[i][j]==val){return false;}}}return true;}void solveSudoku(vector<vector<char>>& board) {backtracking(board);}
};

4.回溯算法总结

代码随想录
**总结：**回溯是递归的副产品，只要有递归就会有回溯，所以回溯法也经常和二叉树遍历，深度优先搜索混在一起，因为这两种方式都是用了递归。

回溯法就是暴力搜索，并不是什么高效的算法，最多再剪枝一下。

回溯算法能解决如下问题：

组合问题：N个数里面按一定规则找出k个数的集合
排列问题：N个数按一定规则全排列，有几种排列方式
切割问题：一个字符串按一定规则有几种切割方式
子集问题：一个N个数的集合里有多少符合条件的子集
棋盘问题：N皇后，解数独等等

回溯法的模板：

void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {处理节点;backtracking(路径，选择列表); // 递归回溯，撤销处理结果}
}