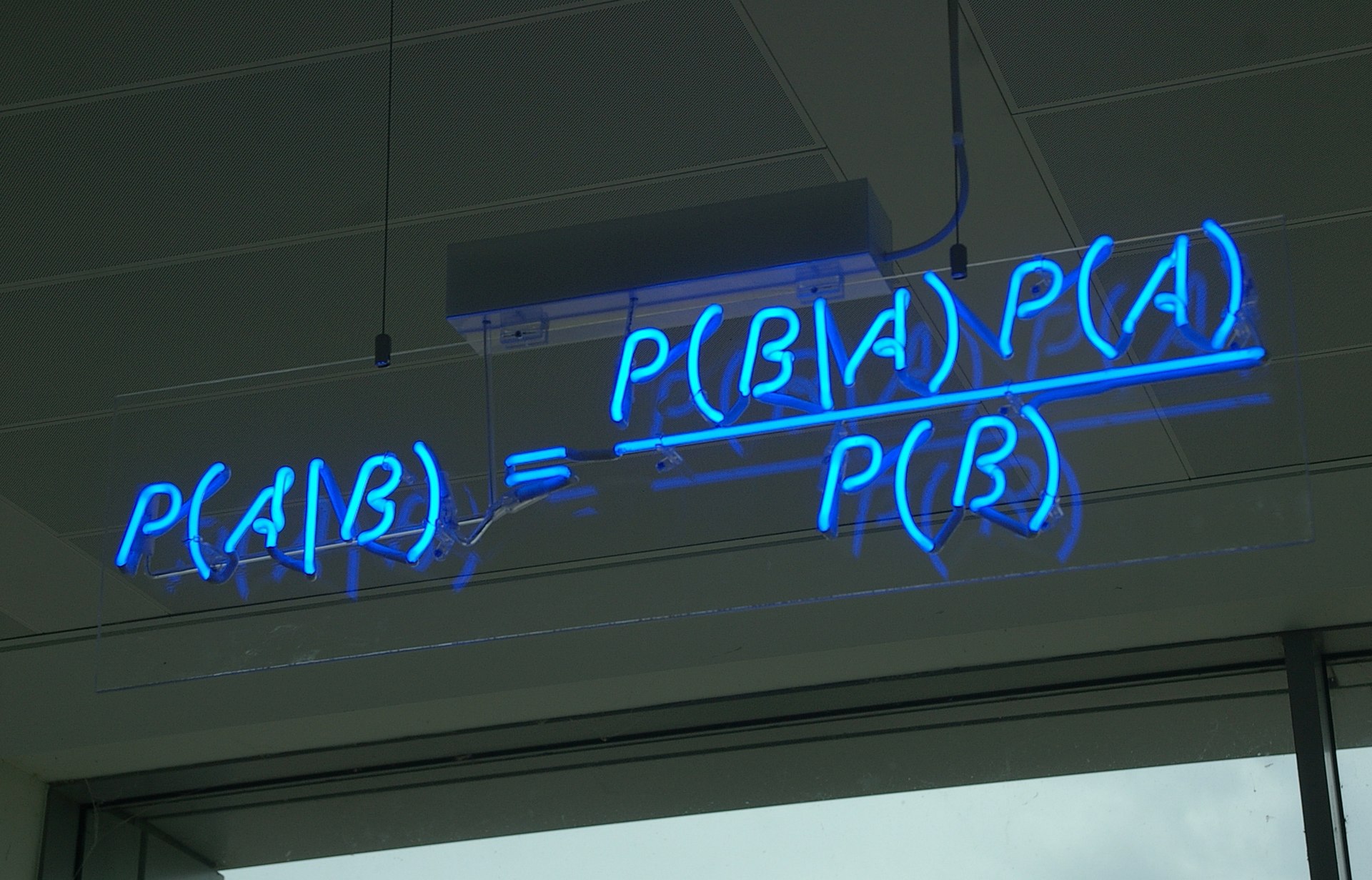生成扩散模型漫谈（二）：DDPM = 自回归式VAE-编程知识

生成扩散模型漫谈（二）：DDPM = 自回归式VAE

news/2024/9/4 22:38:46/文章来源:https://www.cnblogs.com/zhangxianrong/p/18290565

在文章《生成扩散模型漫谈（一）：DDPM = 拆楼 + 建楼》中，我们为生成扩散模型DDPM构建了“拆楼-建楼”的通俗类比，并且借助该类比完整地推导了生成扩散模型DDPM的理论形式。在该文章中，我们还指出DDPM本质上已经不是传统的扩散模型了，它更多的是一个变分自编码器VAE，实际上DDPM的原论文中也是将它按照VAE的思路进行推导的。

所以，本文就从VAE的角度来重新介绍一版DDPM，同时分享一下自己的Keras实现代码和实践经验。

多步突破 #

在传统的VAE中，编码过程和生成过程都是一步到位的：
\begin{equation}\text{编码:}\,\,x\to z\,,\quad \text{生成:}\,\,z\to x\end{equation}
这样做就只涉及到三个分布：编码分布$p(z|x)$、生成分布$q(x|z)$以及先验分布$q(z)$，它的好处是形式比较简单，$x$与$z$之间的映射关系也比较确定，因此可以同时得到编码模型和生成模型，实现隐变量编辑等需求；但是它的缺点也很明显，因为我们建模概率分布的能力有限，这三个分布都只能建模为正态分布，这限制了模型的表达能力，最终通常得到偏模糊的生成结果。

为了突破这个限制，DDPM将编码过程和生成过程分解为$T$步：
\begin{equation}\begin{aligned}&\text{编码:}\,\,\boldsymbol{x} = \boldsymbol{x}_0 \to \boldsymbol{x}_1 \to \boldsymbol{x}_2 \to \cdots \to \boldsymbol{x}_{T-1} \to \boldsymbol{x}_T = \boldsymbol{z} \\
&\text{生成:}\,\,\boldsymbol{z} = \boldsymbol{x}_T \to \boldsymbol{x}_{T-1} \to \boldsymbol{x}_{T-2} \to \cdots \to \boldsymbol{x}_1 \to \boldsymbol{x}_0 = \boldsymbol{x}
\end{aligned}\label{eq:factor}\end{equation}
这样一来，每一个$p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})$和$q(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$仅仅负责建模一个微小变化，它们依然建模为正态分布。可能读着就想问了：那既然同样是正态分布，为什么分解为多步会比单步要好？这是因为对于微小变化来说，可以用正态分布足够近似地建模，类似于曲线在小范围内可以用直线近似，多步分解就有点像用分段线性函数拟合复杂曲线，因此理论上可以突破传统单步VAE的拟合能力限制。

联合散度 #

所以，现在的计划就是通过递归式分解$\eqref{eq:factor}$来增强传统VAE的能力，每一步编码过程被建模成$p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})$，每一步生成过程则被建模成$q(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$，相应的联合分布就是：
\begin{equation}\begin{aligned}&p(\boldsymbol{x}_0, \boldsymbol{x}_1, \boldsymbol{x}_2, \cdots, \boldsymbol{x}_T) = p(\boldsymbol{x}_T|\boldsymbol{x}_{T-1})\cdots p(\boldsymbol{x}_2|\boldsymbol{x}_1) p(\boldsymbol{x}_1|\boldsymbol{x}_0) \tilde{p}(\boldsymbol{x}_0) \\
&q(\boldsymbol{x}_0, \boldsymbol{x}_1, \boldsymbol{x}_2, \cdots, \boldsymbol{x}_T) = q(\boldsymbol{x}_0|\boldsymbol{x}_1)\cdots q(\boldsymbol{x}_{T-2}|\boldsymbol{x}_{T-1}) q(\boldsymbol{x}_{T-1}|\boldsymbol{x}_T) q(\boldsymbol{x}_T)
\end{aligned}\end{equation}
别忘了$\boldsymbol{x}_0$代表真实样本，所以$\tilde{p}(\boldsymbol{x}_0)$就是数据分布；而$\boldsymbol{x}_T$代表着最终的编码，所以$q(\boldsymbol{x}_T)$就是先验分布；剩下的$p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})$、$q(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$就代表着编码、生成的一小步。（提示：经过考虑，这里还是沿用本网站介绍VAE一直用的记号习惯，即“编码分布用$p$、生成分布用$q$”，所以这里的$p$、$q$含义跟DDPM论文是刚好相反的，望读者知悉。）

在《变分自编码器（二）：从贝叶斯观点出发》中笔者就提出，理解VAE的最简洁的理论途径，就是将其理解为在最小化联合分布的KL散度，对于DDPM也是如此，上面我们已经写出了两个联合分布，所以DDPM的目的就是最小化
\begin{equation}KL(p\Vert q) = \int p(\boldsymbol{x}_T|\boldsymbol{x}_{T-1})\cdots p(\boldsymbol{x}_1|\boldsymbol{x}_0) \tilde{p}(\boldsymbol{x}_0) \log \frac{p(\boldsymbol{x}_T|\boldsymbol{x}_{T-1})\cdots p(\boldsymbol{x}_1|\boldsymbol{x}_0) \tilde{p}(\boldsymbol{x}_0)}{q(\boldsymbol{x}_0|\boldsymbol{x}_1)\cdots q(\boldsymbol{x}_{T-1}|\boldsymbol{x}_T) q(\boldsymbol{x}_T)} d\boldsymbol{x}_0 d\boldsymbol{x}_1\cdots d\boldsymbol{x}_T\label{eq:kl}\end{equation}
这就是DDPM的优化目标了。到目前为止的结果，都跟DDPM原论文的结果一样的（只是记号略有不同），也跟更原始的论文《Deep Unsupervised Learning using Nonequilibrium Thermodynamics》一致。接下来，我们就要将$p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})$、$q(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$具体形式定下来，然后简化DDPM的优化目标$\eqref{eq:kl}$。

分而治之 #

首先我们要知道，DDPM只是想做一个生成模型，所以它只是将每一步的编码建立为极简单的正态分布：$p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})=\mathcal{N}(\boldsymbol{x}_t;\alpha_t \boldsymbol{x}_{t-1}, \beta_t^2 \boldsymbol{I})$，其主要的特点是均值向量仅仅由输入$\boldsymbol{x}_{t-1}$乘以一个标量$\alpha_t$得到，相比之下传统VAE的均值方差都是用神经网络学习出来的，因此DDPM是放弃了模型的编码能力，最终只得到一个纯粹的生成模型；至于$q(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$，则被建模成均值向量可学习的正态分布$\mathcal{N}(\boldsymbol{x}_{t-1};\boldsymbol{\mu}(\boldsymbol{x}_t), \sigma_t^2 \boldsymbol{I})$。其中$\alpha_t,\beta_t,\sigma_t$都不是可训练参数，而是事先设定好的值（怎么设置我们稍后讨论），所以整个模型拥有可训练参数的就只有$\boldsymbol{\mu}(\boldsymbol{x}_t)$。（提示：本文$\alpha_t,\beta_t$的定义跟原论文不一样。）

由于目前分布$p$不含任何的可训练参数，因此目标$\eqref{eq:kl}$中关于$p$的积分就只是贡献一个可以忽略的常数，所以目标$\eqref{eq:kl}$等价于
\begin{equation}\begin{aligned}&\,-\int p(\boldsymbol{x}_T|\boldsymbol{x}_{T-1})\cdots p(\boldsymbol{x}_1|\boldsymbol{x}_0) \tilde{p}(\boldsymbol{x}_0) \log q(\boldsymbol{x}_0|\boldsymbol{x}_1)\cdots q(\boldsymbol{x}_{T-1}|\boldsymbol{x}_T) q(\boldsymbol{x}_T) d\boldsymbol{x}_0 d\boldsymbol{x}_1\cdots d\boldsymbol{x}_T \\
=&\,-\int p(\boldsymbol{x}_T|\boldsymbol{x}_{T-1})\cdots p(\boldsymbol{x}_1|\boldsymbol{x}_0) \tilde{p}(\boldsymbol{x}_0) \left[\log q(\boldsymbol{x}_T) + \sum_{t=1}^T\log q(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)\right] d\boldsymbol{x}_0 d\boldsymbol{x}_1\cdots d\boldsymbol{x}_T
\end{aligned}\end{equation}
由于先验分布$q(\boldsymbol{x}_T)$一般都取标准正态分布，也是没有参数的，所以这一项也只是贡献一个常数。因此需要计算的就是每一项
\begin{equation}\begin{aligned}&\,-\int p(\boldsymbol{x}_T|\boldsymbol{x}_{T-1})\cdots p(\boldsymbol{x}_1|\boldsymbol{x}_0) \tilde{p}(\boldsymbol{x}_0) \log q(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t) d\boldsymbol{x}_0 d\boldsymbol{x}_1\cdots d\boldsymbol{x}_T\\
=&\,-\int p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})\cdots p(\boldsymbol{x}_1|\boldsymbol{x}_0) \tilde{p}(\boldsymbol{x}_0) \log q(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t) d\boldsymbol{x}_0 d\boldsymbol{x}_1\cdots d\boldsymbol{x}_t\\
=&\,-\int p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_0) \tilde{p}(\boldsymbol{x}_0) \log q(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t) d\boldsymbol{x}_0 d\boldsymbol{x}_{t-1}d\boldsymbol{x}_t
\end{aligned}\end{equation}
其中第一个等号是因为$q(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$至多依赖到$\boldsymbol{x}_t$，因此$t+1$到$T$的分布可以直接积分为1；第二个等号则是因为$q(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$也不依赖于$\boldsymbol{x}_1,\cdots,\boldsymbol{x}_{t-2}$，所以关于它们的积分我们也可以事先算出，结果为$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_0)=\mathcal{N}(\boldsymbol{x}_{t-1};\bar{\alpha}_{t-1} \boldsymbol{x}_0, \bar{\beta}_{t-1}^2 \boldsymbol{I})$，该结果可以参考下一节的式$\eqref{eq:x0-xt}$。

场景再现 #

接下来的过程就跟上一篇文章的“又如何建”一节基本上是一样的了：

1、除去优化无关的常数，$-\log q(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$这一项所贡献的就是$\frac{1}{2\sigma_t^2}\left\Vert\boldsymbol{x}_{t-1} - \boldsymbol{\mu}(\boldsymbol{x}_t)\right\Vert^2$；

2、$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_0)$意味着$\boldsymbol{x}_{t-1} = \bar{\alpha}_{t-1}\boldsymbol{x}_0 + \bar{\beta}_{t-1}\bar{\boldsymbol{\varepsilon}}_{t-1}$，$p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})$又意味着$\boldsymbol{x}_t = \alpha_t \boldsymbol{x}_{t-1} + \beta_t \boldsymbol{\varepsilon}_t$，其中$\bar{\boldsymbol{\varepsilon}}_{t-1},\boldsymbol{\varepsilon}_t\sim \mathcal{N}(\boldsymbol{0},\boldsymbol{I})$；

3、由$\boldsymbol{x}_{t-1} = \frac{1}{\alpha_t}\left(\boldsymbol{x}_t - \beta_t \boldsymbol{\varepsilon}_t\right)$则启发我们将$\boldsymbol{\mu}(\boldsymbol{x}_t)$参数化为$\boldsymbol{\mu}(\boldsymbol{x}_t) = \frac{1}{\alpha_t}\left(\boldsymbol{x}_t - \beta_t \boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)\right)$。

这一系列变换下来，优化目标等价于
\begin{equation}\frac{\beta_t^2}{\alpha_t^2\sigma_t^2}\mathbb{E}_{\bar{\boldsymbol{\varepsilon}}_{t-1},\boldsymbol{\varepsilon}_t\sim \mathcal{N}(\boldsymbol{0},\boldsymbol{I}),\boldsymbol{x}_0\sim \tilde{p}(\boldsymbol{x}_0)}\left[\left\Vert \boldsymbol{\varepsilon}_t - \boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\bar{\alpha}_t\boldsymbol{x}_0 + \alpha_t\bar{\beta}_{t-1}\bar{\boldsymbol{\varepsilon}}_{t-1} + \beta_t \boldsymbol{\varepsilon}_t, t)\right\Vert^2\right]\end{equation}
随后按照“降低方差”一节做换元，结果就是
\begin{equation}\frac{\beta_t^4}{\bar{\beta}_t^2\alpha_t^2\sigma_t^2}\mathbb{E}_{\boldsymbol{\varepsilon}\sim \mathcal{N}(\boldsymbol{0},\boldsymbol{I}),\boldsymbol{x}_0\sim \tilde{p}(\boldsymbol{x}_0)}\left[\left\Vert\boldsymbol{\varepsilon} - \frac{\bar{\beta}_t}{\beta_t}\boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\bar{\alpha}_t\boldsymbol{x}_0 + \bar{\beta}_t\boldsymbol{\varepsilon}, t)\right\Vert^2\right]\label{eq:loss}\end{equation}
这就得到了DDPM的训练目标了（原论文通过实验发现，去掉上式前面的系数后实际效果更好些）。它是我们从VAE的优化目标出发，逐步简化积分结果得到的，虽然有点长，但每一步都是有章可循的，有计算难度，但没有思路上的难度。

相比之下，DDPM的原论文中，很突兀引入了一个$q(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t,\boldsymbol{x}_0)$（原论文记号）来进行裂项相消，然后转化为正态分布的KL散度形式。整个过程的这一步技巧性太强，显得太过“莫名其妙”，对笔者来说相当难以接受。

超参设置 #

这一节我们来讨论一下$\alpha_t,\beta_t,\sigma_t$的选择问题。

对于$p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})$来说，习惯上约定$\alpha_t^2 + \beta_t^2=1$，这样就减少了一半的参数了，并且有助于简化形式，这其实在上一篇文章我们已经推导过了，由于正态分布的叠加性，在此约束之下我们有
\begin{equation}p(\boldsymbol{x}_t|\boldsymbol{x}_0) = \int p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})\cdots p(\boldsymbol{x}_1|\boldsymbol{x}_0) d\boldsymbol{x}_1\cdots d\boldsymbol{x}_{t-1} = \mathcal{N}(\boldsymbol{x}_t;\bar{\alpha}_t \boldsymbol{x}_0, \bar{\beta}_t^2 \boldsymbol{I})\label{eq:x0-xt}\end{equation}
其中$\bar{\alpha}_t = \alpha_1\cdots\alpha_t$，而$\bar{\beta}_t = \sqrt{1-\bar{\alpha}_t^2}$，这样一来$p(\boldsymbol{x}_t|\boldsymbol{x}_0)$就具有比较简约的形式。可能读者又想问事前是怎么想到$\alpha_t^2 + \beta_t^2=1$这个约束呢？我们知道$\mathcal{N}(\boldsymbol{x}_t;\alpha_t \boldsymbol{x}_{t-1}, \beta_t^2 \boldsymbol{I})$意味着$\boldsymbol{x}_t = \alpha_t \boldsymbol{x}_{t-1} + \beta_t \boldsymbol{\varepsilon}_t,\boldsymbol{\varepsilon}_t\sim \mathcal{N}(\boldsymbol{0},\boldsymbol{I})$，如果$\boldsymbol{x}_{t-1}$也是$\sim \mathcal{N}(\boldsymbol{0},\boldsymbol{I})$的话，我们就希望$\boldsymbol{x}_t$也是$\sim \mathcal{N}(\boldsymbol{0},\boldsymbol{I})$，所以就确定了$\alpha_t^2+\beta_t^2=1$了。

前面说了，$q(\boldsymbol{x}_T)$一般都取标准正态分布$\mathcal{N}(\boldsymbol{x}_T;\boldsymbol{0}, \boldsymbol{I})$。而我们的学习目标是最小化两个联合分布的KL散度，即希望$p=q$，那么它们的边缘分布自然也相等，所以我们也希望
\begin{equation}q(\boldsymbol{x}_T) = \int p(\boldsymbol{x}_T|\boldsymbol{x}_{T-1})\cdots p(\boldsymbol{x}_1|\boldsymbol{x}_0) \tilde{p}(\boldsymbol{x}_0) d\boldsymbol{x}_0 d\boldsymbol{x}_1\cdots d\boldsymbol{x}_{T-1} = \int p(\boldsymbol{x}_T|\boldsymbol{x}_0) \tilde{p}(\boldsymbol{x}_0) d\boldsymbol{x}_0 \end{equation}
由于数据分布$\tilde{p}(\boldsymbol{x}_0)$是任意的，所以要使上式恒成立，只能让$p(\boldsymbol{x}_T|\boldsymbol{x}_0)=q(\boldsymbol{x}_T)$，即退化为与$\boldsymbol{x}_0$无关的标准正态分布，这意味着我们要设计适当的$\alpha_t$，使得$\bar{\alpha}_T\approx 0$。同时这再次告诉我们，DDPM是没有编码能力了，最终的$p(\boldsymbol{x}_T|\boldsymbol{x}_0)$可以说跟输入$\boldsymbol{x}_0$无关的。用上一篇文章的“拆楼-建楼”类比就是说，原来的楼已经被完全拆成原材料了，如果用这堆材料重新建楼的话，可以建成任意样子的楼，而不一定是拆之前的样子。DDPM取了$\alpha_t = \sqrt{1 - \frac{0.02t}{T}}$，关于该选择的性质，我们在上一篇文章的“超参设置”一节也分析过了。

至于$\sigma_t$，理论上不同的数据分布$\tilde{p}(\boldsymbol{x}_0)$来说对应不同的最优$\sigma_t$，但我们又不想将$\sigma_t$设为可训练参数，所以只好选一些特殊的$\tilde{p}(\boldsymbol{x}_0)$来推导相应的最优$\sigma_t$，并认为由特例推导出来的$\sigma_t$可以泛化到一般的数据分布。我们可以考虑两个简单的例子：

1、假设训练集只有一个样本$\boldsymbol{x}_*$，即$\tilde{p}(\boldsymbol{x}_0)$是狄拉克分布$\delta(\boldsymbol{x}_0 - \boldsymbol{x}_*)$，可以推出最优的$\sigma_t = \frac{\bar{\beta}_{t-1}}{\bar{\beta}_t}\beta_t$；

2、假设数据分布$\tilde{p}(\boldsymbol{x}_0)$服从标准正态分布，这时候可以推出最优的$\sigma_t = \beta_t$。

实验结果显示两个选择的表现是相似的，因此可以选择任意一个进行采样。两个结果的推导过程有点长，我们后面再择机讨论。

参考实现 #

这么精彩的模型怎么可以少得了Keras实现？下面提供笔者的参考实现：

Github地址：https://github.com/bojone/Keras-DDPM

注意，笔者的实现并非严格按照DDPM原始开源代码来进行，而是根据自己的设计简化了U-Net的架构（比如特征拼接改为相加、去掉了Attention等），使得可以快速出效果。经测试，在单张24G显存的3090下，以blocks=1,batch_size=64训练128*128大小的CelebA HQ人脸数据集，半天就能初见成效。训练3天后的采样效果如下：

笔者训练的DDPM采样结果演示

在调试过程中，笔者总结出了如下的实践经验：

1、损失函数不能用mse，而必须用欧氏距离，两者的差别是mse在欧氏距离基础上除以图片的$\text{宽}\times\text{高}\times\text{通道数}$，这会导致损失值过小，部分参数的梯度可能会被忽略为0，从而导致训练过程先收敛后发散，该现象也经常出现于低精度训练中，可以参考《在bert4keras中使用混合精度和XLA加速训练》；

2、归一化方式可以用Instance Norm、Layer Norm、Group Norm等，但不要用Batch Norm，因为Batch Norm存在训练和推理不一致的问题，可能出现训练效果特别好，预测效果特别差的问题；

3、网络结构没有必要照搬原论文，原论文是为了刷SOTA发论文，照搬的话肯定是又大又慢的，只需要按照U-Net的思路设计自编码器，就基本上可以训练出个大概效果了，因为就相当于是个纯粹的回归问题，还是很好训练的；

4、关于参数$t$的传入，原论文用了Sinusoidal位置编码，笔者发现直接换为可训练的Embedding，效果也差不多；

5、按照以往搞语言模型预训练的习惯，笔者用了LAMB优化器，它更方便调学习率，基本上$10^{-3}$的学习率可以适用于任意初始化方式的模型训练。

综合评价 #

结合《生成扩散模型漫谈（一）：DDPM = 拆楼 + 建楼》和本文的介绍，想必读者都已经对DDPM有自己的看法了，能基本看出DDPM优点、缺点以及相应的改进方向在哪了。

DDPM的优点很明显，就是容易训练，并且生成的图片也清晰。这个容易训练是相对GAN而言的，GAN是一个$\min\text{-}\max$过程，训练中的不确定性很大，容易崩溃，而DDPM就纯粹是一个回归的损失函数，只需要纯粹的最小化，因此训练过程非常平稳。同时，经过“拆楼-建楼”的类比，我们也可以发现DDPM在通俗理解方面其实也不逊色于GAN。

不过，DDPM的缺点也很明显。首先最突出的就是采样速度太慢，需要执行模型$T$步（原论文$T=1000$才能完成采样），可以说这比GAN的一步到位的采样要慢上$T$倍，后面有很多工作对这一点进行改进；其次，在GAN中，从随机噪声到生成样本的训练是一个确定性的变换，随机噪声是生成结果的一个解耦的隐变量，我们可以进行插值生成，或者对之编辑以实现控制生成等，但是DDPM中生成过程是一个完全随机的过程，两者没有确定性的关系，这种编辑生成就不存在了。DDPM原论文虽然也演示了插值生成效果，但那只是在原始图片上进行插值的，然后通过噪声来模糊图片，让模型重新“脑补”出新的图片，这种插值很难做到语义上的融合。

除了针对上述缺点来做改进外，DDPM还有其他一些可做的方向，比如目前演示的DDPM都是无条件的生成，那么很自然就想到有条件的DDPM的，就好比从VAE到C-VAE、从GAN到C-GAN一样，这也是当前扩散模型的一个主流应用，比如用Google的Imagen就同时包含了用扩散模型做文本生成图片以及做超分辨率，这两者本质上就是条件式扩散模型了；再比如，目前的DDPM是为连续型变量设计的，但从其思想来说应该也是适用于离散型数据的，那么离散型数据的DDPM怎么设计呢？