2024 暑假集训笔记

Day 1

---

搜索

DFS：

基本思路：

1. 边界设置(if(...) return ;)
2. 检查(for(....))
3. 标记结果(a[...]=...)
4. 递归搜索(dfs(...))
5. 回溯

例题：

N皇后问题

[POJ 1321] 棋盘问题

[POJ 1011] Sticks

BFS

略

---

分治

基本思路

1. 将处理区间二分为两个区间(merge(l,mid) merge(mid+1,r))
2. 边界(if(l==r) return ;)
3. 对两个区间进行处理(while(ptr1<=mid&&ptr2<=r) ....)
4. 合并(for(int i=l;i<=r;i++) ..[i]=..[i];)

归并排序

void merge(int l,int r){if(l==r){return ;}int mid=(l+r)/2;merge(l,mid);merge(mid+1,r);int prt1=l,prt2=mid+1;int prt3=l;while(prt1<=mid&&prt2<=r){if(a[prt1]<=a[prt2]){b[prt3]=a[prt1];prt1++;prt3++;}else{b[prt3]=a[prt2];ans+=mid+1-prt1;prt2++;prt3++;}}while(prt1<=mid){b[prt3]=a[prt1];prt1++;prt3++;}while(prt2<=r){b[prt3]=a[prt2];prt2++;prt3++;}for(int i=l;i<=r;i++){a[i]=b[i];}
}

求逆序对

仅将

	else{b[prt3]=a[prt2];prt2++;prt3++;}

中添加：
ans+=mid+1-prt1;

例题：

逆序对

最大子段和

[Luogu P1228] 地毯填补问题

平面最近点对

---

Day2

单调栈

适用于求某数左/右边的第一个大于它的数

思路：

1. 维护栈内单调性(pop掉所有比它小或大的数)
2. 记录栈首，即记录答案(因为比它小/大的数已经被pop掉，所以剩下那个数就是答案)
3. 将该数入栈

例题：

P1901 发射站

用单调栈求出每个数发射出的能量被接收到了哪里，记录每个数接收到的能量，求最大值即可

---

单调队列

适用于【滑动窗口】题型

思路

1. 维护队内单调性(从队尾pop掉所有比它小或大的数)
2. 将该数从队尾入队
3. 检测队首的数是否还在窗口内，将“过期”的数从队首pop掉
4. 记录队首，即记录答案(因为比它小/大的数已经被pop掉，所以剩下那个数就是答案)

例题

P1886 滑动窗口

略

---

堆

小根堆：priority_queue<int,vector<int>,greater<int> > q;

其余不再阐述

哈夫曼树

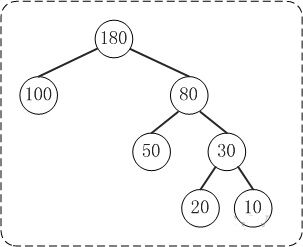
节点值为左儿子+右儿子，叶子为给定序列中的值

例题

P1090 合并果子

每次选取最小的两堆合并，证明略

---

线段树

一种支持区间快速操作/查询的高级数据结构

朴素线段树

思路

1. 建树(build)
2. 单点修改(change1)
3. 区间修改(change2，需用到懒标记（Lazy Mark)来降低单次修改的时间
4. 查询(query)

详见 day2\线段树.cpp

其他线段树

动态开点线段树

当总点数十分多（1e9),有值的点数却十分少（1e5），可以只开那些有值的点，保留空间

可持久化线段树（主席树）

在动态开点线段树的基础上能够保存历史版本的线段树

---

树状数组

能够在O(logn)内单点/区间修改,并求区间和。比线段树代码更简单，但不易变通

性质：

lowbit()运算

取数二进制最低位的1

例如，92二进制为1011100，那么lowbit(92)的二进制为100，即8

树状数组一个节点维护的区间为[p-lowbit(p)+1,p]

一个节点的父节点为p+lowbit(p)。

修改

从子到父依次修改即可

void change(int pos,int dlt){for(;pos<=n;pos+=pos&(-pos)){t[pos]+=dlt;}
}

查询

类似前缀和（t[i]存储着前i个数的和），区间查找照葫芦画瓢即可

int query(int pos){int ans=0;for(;pos>=1;pos-=pos&(-pos)){ans+=t[pos];}return ans;
}

---

Day3

数据结构（待补）

ST表(RMQ问题)

LCA

BST二叉搜索树

并查集

动态规划

一维DP

背包DP

01背包

例题：P1048 采药

给定一堆只有一个的物品，每个物品都有其特有的价值和代价(重量或时间)。求在只能付出给定代价时，能够获得的最大价值为多少

由于每个物品有0或1（选或不选）的状态，称此类问题为01背包问题。

设f[i][j]为已经选了i个物品，背包剩余j单位的重量或时间时，能获得的最大代价。

对于每个物品都有选和不选的情况，所以可以推出:(w[i]代表第i个物品的代价,v[i]代表第i个物品的价值)

选:f[i][j]=f[i-1][j-w[i]]+v[i](选这个物品代表背包的剩余容积减去相应的重量，加上总价值)
不选:f[i][j]=f[i-1][j]
总：f[i][j]=max(f[i-1][j-w[i]]+v[i],f[i-1][j])

观察可得，每个一个状态的转移只与[i-1]有关，因此可以转化为一维来优化————滚动数组

例题代码：

const int N=100+5;
int n,m;
int t[N],v[N];
int f[N*10];
signed main()
{//faster();cin>>m>>n;for(int i=1;i<=n;i++){cin>>t[i]>>v[i];}for(int i=1;i<=n;i++){for(int j=m;j>=t[i];j--){f[j]=max(f[j-t[i]]+v[i],f[j]);}}cout<<f[m];return 0;
}

---

Day4（待补）

树形DP

树上背包

前缀和优化

高维前缀和

差分

Day5（待补）

筛法：

朴素筛法

线性筛法

区间筛法

最小生成树

kruskal

prim

---

Day6

最短路

Floyd

求多源最短路的算法，思想类似于动态规划

求最短路

• 令f[i][j][k]点i到点j(不包含i，j）由编号不大于k的点组成的最短路路径。

• 考虑将f[i][j][k]转移至f[i][j][k+1]。

• 分两种情况：

• 1. 转移后的路径上编号仍小于等于k。==>f[i][j][k+1]=f[i][j][k];
• 2. 从i到k+1，再从k+1到j。==>f[i][j][k+1]=f[i][k+1][k]+f[k+1][j][k];

• 由此可推出转移方程f[i][j][k+1]=min(f[i][j][k],f[i][k+1][k]+f[k+1][j][k]);

• 边界：f[i][j][0]=edge(i,j);

• 目标：f[i][j][n]为 i 到 j 的最短路。

注意到，每一次状态的转移只与 k+1 和 k 有关，因此用滚动数组可以省去 k 这个第三维度。

dijkstra

• 设dist[i]为从起点到第 \(i\) 个点的最短路
• 除起点dist值为0以外，其余点的值为+inf
• 每次从dist数组中取dist最小的点来更新其它点的最短路(dist[i]=dist[j]+edge(i,j),\(i\) 为待更新的点，\(j\) 为当前dist值最小的点)————松弛操作
• 当所有的点都被取完一遍后，结束求解
• n个点,m条边。时间复杂度为\(O(n^2m)\)

强连通分量

边的分类

返祖边：由后代指向它的祖先

横插边：由一个节点指向它的兄弟或兄弟的后代(必须为从左往右)

树边：原先树上的边

非树边：即返祖边和横插边