Lecture 07 Real-time Global Illumination (in 3D)

news/2024/11/15 15:06:23/文章来源:https://www.cnblogs.com/Tellulu/p/18391225

Lecture 07 Real-time Global Illumination (in 3D)

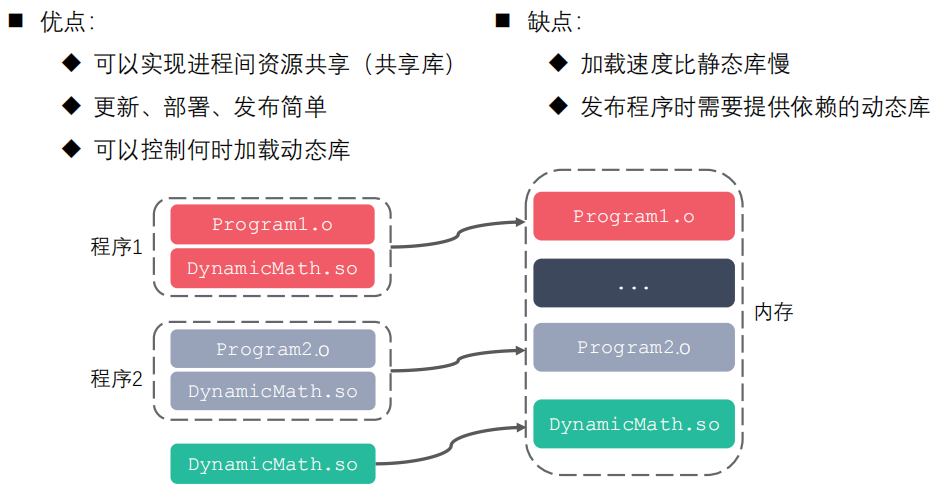
实时渲染中全局光照一般只bounce两次（直接光照bounce一次，间接光照bounce两次）

primary light source 真正的光源
secondary light source 次级光源：

一切被直接光照照到的物体都会继续将自己作为光源
想要用间接光照照亮\(p\)点，需要知道什么？
- 哪些是次级光源（或者说哪些物体表面会被直接光照照到）
  - 可以通过Shadow Map来回答
- 点\(p\)接收到各次级光源的贡献是多少？
  - 每个次级光源的物体表面反射出的光有一个radiance和area 范围
    
    也就是要解一个Area light的渲染方程

Reflective Shadow Maps (RSM)

次级光源的表达形式

Shadow Map可以完美解决第一个问题，如果有一个Area light，可以用soft shadow mapping来得到不同的点的入射光强度

Shadow Map中的每一个texel可以认为是场景中的一个小片，那么对于一个\(m\times n\) 的shadow map，自然可以认为是有\(m\times n\)个次级光源，也就是要计算用\(m\times n\)个次级光源照亮点\(p\)

虽然计算量太大，但是shadow map给了我们一个场景中次级光源的离散表达方式
次级光源对点\(p\) shading时的方向

要计算点\(p\)接收到次级光源的radiance，实际上是从点\(p\)出发观察，那么这个观察方向是不固定的，于是认为所有的reflector 反射物都是diffuse的（不是要求接收物点\(p\)是diffuse的），就无所谓观察方向了

至此知道了场景中哪些是次级光源，也知道了次级光源反射出的能量是多少，解决了问题一

RSM其实类似于一个光栅化版本的离线渲染中的Virtual Point Light，更广义的说，VPL属于Instance Radiosity 即时辐射度/实时辐射度

最早即时辐射度不是基于光线追踪，而VPL将即时辐射度和光线追踪结合得非常好

Recall: Light Measurements of Interest 辐射度量学

Flux/Power：描述能量是多少
Radiant Intensity: 描述一个单位立体角上对应的能量是多少
Irradiance: 描述一个单位面积下对应的能量
Radiance: 单位立体角单位面积上对应的能量

公式推导

\[L_o(p,\omega_o)=\int_{\Omega_{patch}}L_i(p,\omega_i)V(p,\omega_i)f_r(p,\omega_i,\omega_o)\cos\theta_id\omega_i\\ =\int_{A_{patch}}L_i(q\rightarrow p)V(p,\omega_i)f_r(p,q\rightarrow p,w_o)\frac{\cos\theta_p\cos\theta_q}{{\lvert\lvert q-p\rvert\rvert}^2}dA\\ 这里通过变量替换，将立体角的积分描述成对Area的积分（对Light的积分）\\ L_i(q\rightarrow p)描述了从q点到p点的radiance是多少\\ \]

先考虑一个patch贡献的光照，如果Area积分面积比较小，可以不用积分，直接乘上Area面积\(\Delta A\)（黎曼积分把一个区间划分得足够小了之后，区间内的积分结果可以通过取区间中的某一个位置近似）

对于Diffuse的reflective patch（上面公式中的\(q\)点）

BRDF项: \(f_r=\rho/\pi\)，\(\rho\)是albedo
Light项: \(L_i=f_r\cdot \frac{\Phi}{dA}\)，\(\Phi\)是incident flux，由光源决定

BRDF的定义：出射的Radiance除以入射的Irradiance，Irradiance等于flux除以面积

这样的好处是将积分中的\(dA\)消掉了

对于reflector，它的BRDF项\(f_r\)是常数，而\(f_r\cdot\Phi\)是人们平常所说的reflected flux

那么对于shadow map中的一个texel，我们要求其\(L_i\)，实际要的就是\(f_r\cdot\Phi\)，这样甚至都不需要知道这个patch对应的大小是多少，因为\(L_i\)项和积分中的\(dA\)消了

所以每个texel只需存一个数就好(\(f_r\cdot\Phi\))
因此

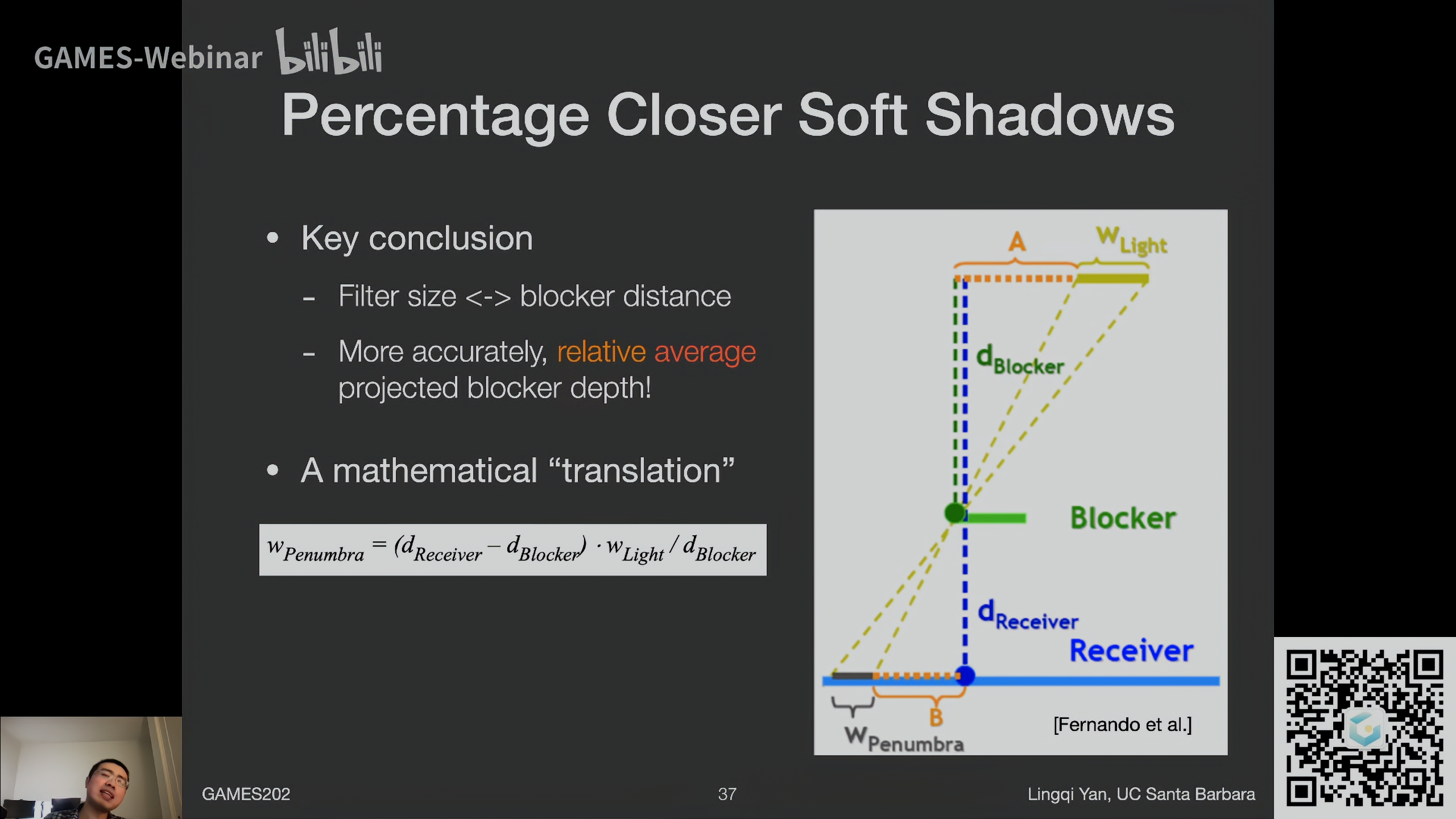
\[E_p(x,n)=\Phi_p\frac{max\{0,<n_p\vert x-x_p>\} max\{0,<n\vert x_p-x>\}}{{\lvert\lvert x-x_p\rvert\rvert}^4}\\\Phi_p=f_r\cdot\Phi\ \\ 这里的x为shading\ point，x_p为次级光源，与渲染方程中的点相反\\ n和n_p为各自的法线\\ 算出的E_p没有考虑Visibility，对应渲染方程中的: L_i(q\rightarrow p)\frac{\cos\theta_p\cos\theta_q}{{\lvert\lvert q-p\rvert\rvert}^2}dA\\ \]
- 分母为什么是四次方不是渲染方程中的平方？因为分子点乘没有normalize
如果考虑次级光源到shading point点\(p\)的可见性Visibility，又是一个\(n^2\)问题，不可能每个次级光源都生成一张shadow map，所以就不考虑可见性了

并非RSM中的每一个texel都对shading point有贡献

首先是Vibility的问题（但是很难算，所以不考虑了，并且间接光照不像直接光照那么高频，影响也不大）
方向上

比如\(x_{-1}\)对应的patch在桌面上，其法线与连线\(x_{-1}x\)夹角\(\cos\)值为负，说明照不到\(x\)点

这已经在渲染方程中体现了（\(E_p\)式中的分子上两项求夹角\(\cos\)值）
距离

本来经过一个距离平方，贡献就已经非常少了，那么给定一个shading point，只用找足够近的次级光源就OK了，于是就引出一个技巧
- 如何找离shading point近的次级光源？
  
  在世界坐标下不好找，那么就将shading point投影到shadow map上，找周围的次级光源
  
  （这里是一个比较大胆的假设，认为shadow map上离得比较近的点或深度接近的点在世界坐标下也接近）
- 为什么要这么做？
  
  加速。
  
  工业界的trick：
  
  即便如此可能也会面临范围比较大的查询，可以根据离texel离shading point的距离决定哪些地方多采一点哪些地方少采一点（越近采样越密），采样少的地方说明将许多texel当成一个，权重应该要更大。这样做可以从原先\(512^2\)次查询降低至\(400\)（举例）

RSM中存什么

深度
世界坐标（世界坐标可以通过深度重建出来，这里是空间换时间）
法线（算\(\cos\)项）
flux（跟光源相关的属性）
等等

RSM的应用

比如手电筒，因为手电筒覆盖的范围比较小，这样RSM的分辨率可以比较低

优缺点

优点
- 容易实现，就是Shadow Map的流程
  
  第一个Pass生成RSM，第二个Pass shading
缺点
- 性能跟光源数量线性相关
  
  有多少光源就得做多少个RSM
- 没有考虑间接光照的Visibility
- 很多假设：
  - 假设reflector是diffuse的
  - 将Shadow Map上的距离能一定程度反映出实际的距离
- 采样率和质量之间的折衷

为什么RSM是3D空间的方法而不是图像空间的方法？

我们需要的RSM在第一趟Pass就已经生成完了，第二个bounce正常从camera渲染就能得到结果，所以其实RSM应该是一个图像空间的方法，但为什么还是归类为3D空间上的方法呢？

因为RSM方法不会受到camera pass是否可见造成的信息影响，换句话说就是理论上不存在一开始就记录不到而丢失信息的情况，这种情况是图像空间呈现的问题
后面的LPV是建立在RSM的基础上

Light Propagation Volumes (LPV)

Key problem
- 查询任何shading point来自四面八方的radiance
Key idea
- Radiance沿直线传播，且不会改变
- 平方衰减？
  
  平方衰减是因为能量在传播过程中面积不断增大，单位面积上intensity会平方衰减，这是另外一个概念
Key solution
- 使用一个3D grid网格分割场景，每个格子称为Voxel体素，光线沿体素传播

步骤

Generation

生成radiance点集（次级光源，同RSM）
- 找到被直接光照照到的表面
- 直接用RSM
Injection

将次级光源点Injection注入到三维网格中的网格中
- 工业界一般用三维纹理来记录grid
- 对每一个grid cell，找到其包含的次级光源
- 将其包含的次级光源各个朝向的radiance分别加起来（朝向可能各不相同），得到任意一个空间上的格子，它往四面八方的radiance的初始值是多少
- 将结果投影至2阶球谐函数（4个基函数）
Propagation

由第2步知道了radiance起点，就可以在三维网格中传播radiance，传播完成后，就知道了任意一个网格中的radiance是多少了
- 对于每个grid cell，收集来自周围6个面的radiance
- 将结果加起来，用球谐函数表示
- 重复若干次直到Volume变得稳定（一般迭代四五次即可）
Rendering

用最终得到的LPV来渲染
- 对于每个shading point，找到其所在grid
- 获取其接收到的所有方向上的incident radiance
- 渲染

问题

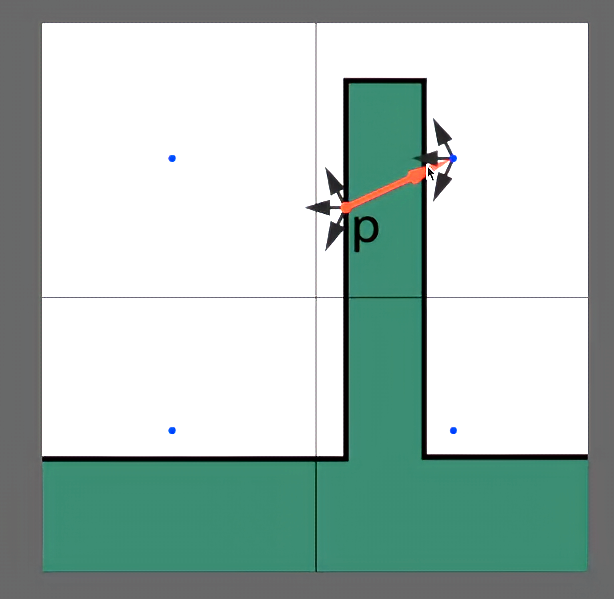
Light leaking

左边的p点接收到了直接光照，但p点反射出的radiance不应该反射到右侧墙体，这样导致了右侧墙体获得了错误的radiance

原因：Voxel的粒度比一个几何物体的粒度大，如果voxel划分地足够小可以避免这个问题（存储问题、propagation时传播的格子数也增多了）
Visibility

不考虑传播时，一个格子能够看到旁边的格子吗？

这里不考虑Visibility，否则计算量太大
斜对角的格子不考虑吗？

不考虑，假设有左下和右上两个斜对角的格子，右上的格子先传播到左边的格子，再传播到下面的格子，和直接斜对角传播一样
自适应分割

工业界会使用不同分辨率的格子来计算
格子多少合适？

一般比场景中的像素少一个数量级
传播过程一定会收敛达到一个稳态吗？

会，类比涟漪，没有施加外力，光线传播一定会达到稳态
烟雾里的传播

在烟雾里光线不沿直线传播
LPV并不是预计算的方法，而是实时的
球谐函数

因为使用SH来记录radiance，所以相当于只能处理diffuse情况，处理glossy情况会糊掉，相当于diffuse了

Voxel Global Illumination (VXGI)

VXGI也是一个two-pass的算法
与RSM的主要区别
- RSM中次级光源是每个像素表示的微小表面，VXGI中场景完成离散化成体素
- 第二个pass从camera出发，打到任何一个像素上，根据这个像素的材质，如glossy材质
  
  camera ray打到glossy材质会变成类似一个锥形往外反射，再根据锥形相交的体素，就知道这些体素的贡献了。对于每个像素都做一遍cone tracing

步骤

将场景体素化
创建hierarchy 层次结构
Pass 1 from the light
- 存储每个体素的incident light的分布，光源从哪些范围来，继承这样一个分布
- 存储法线的分布
- 更新在hierarchy
- 这样不同材质的shading point可以根据这些信息来计算，而不是想LPV一样认为每个voxel都是diffuse的
- 更高层级的voxel将低层级的voxel考虑在一块
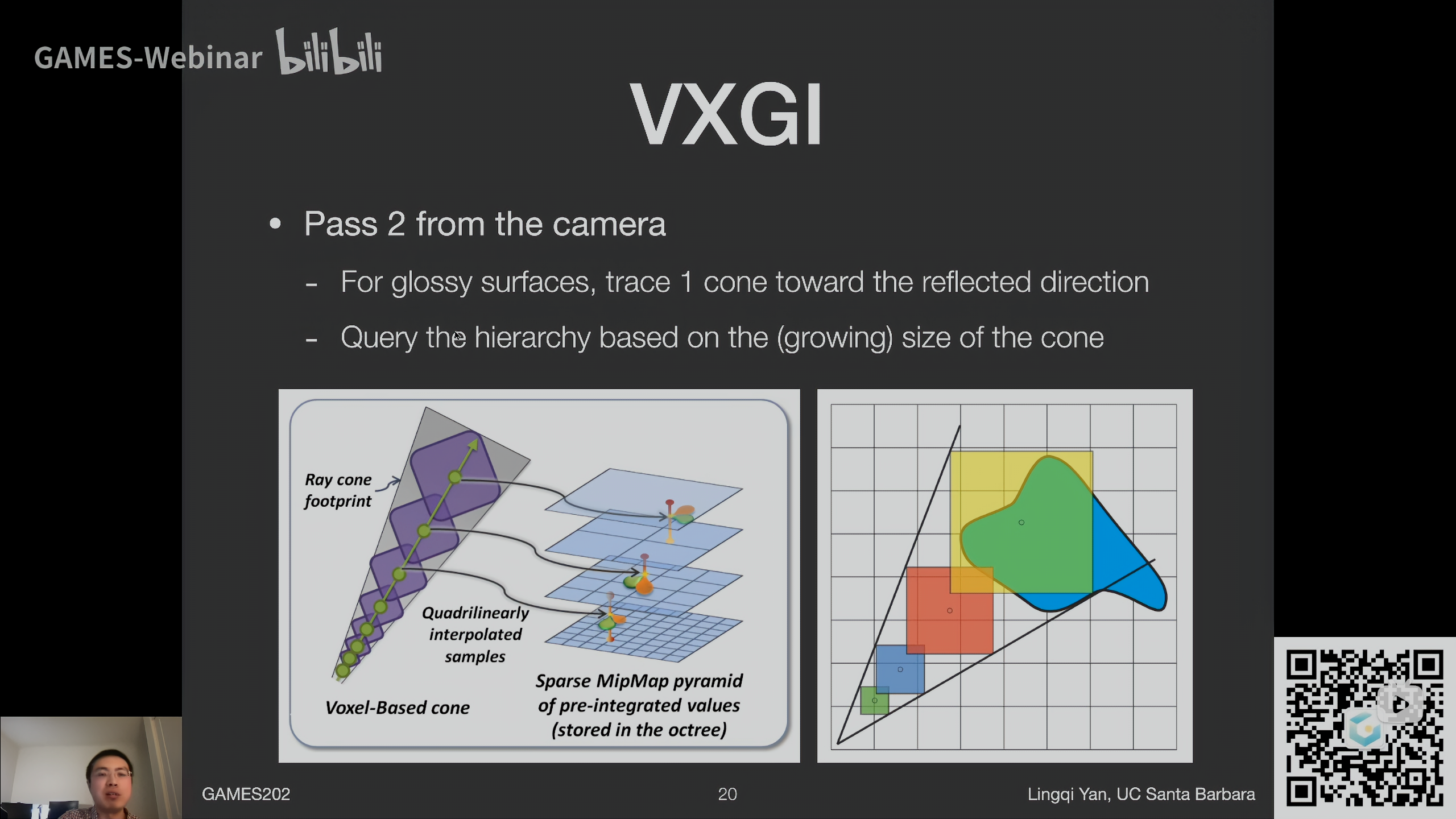
Pass 2 from the camera
- 从shading point出发连出一个锥，场景中所有voxel测试是否与锥相交，相交的话将该voxel的贡献算出来（这样太慢了！）
- 根据圆锥上一个点离初始点的距离算出来一个范围，然后在hierarchy上找对应的层级，这样可以省去每次都查最小的体素的时间
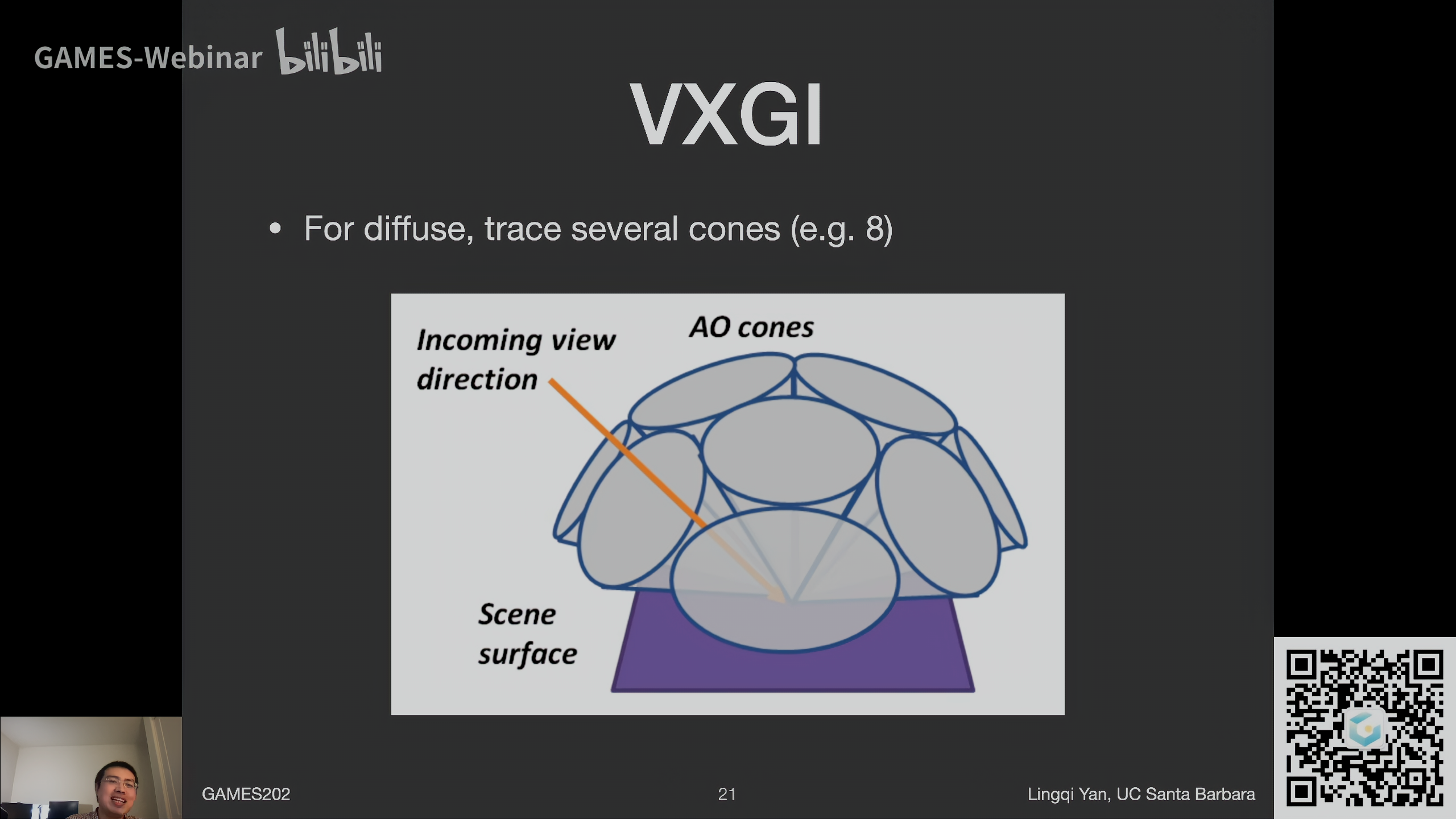
- 如果是diffuse，camera ray反射出的光线是一个半球，那不是场景中所有体素都被考虑进来了吗？
  
  要考虑成一个超大号的圆锥（半球），不如考虑成若干个小圆锥
  - 圆锥和圆锥之间会有缺口
  - 圆锥和圆锥之间可能会有重叠
  - 这些对于diffuse来说影响不大