概述
oftmax函数的表达式 $ \text{Softmax}(x_i) = \frac{e^{x_i}}{\sum_{j} e^{x_j}} $,但在计算机的运算上有一定的缺陷。这个缺陷就是溢出问题。
softmax函数的实现中要进行指数函数的运算,但是此时指数函数的值很容易变得非常大。比如,e^{10} 的值会超过20000,
e^{100} 会变成一个后面有40多个0的超大值, e^{1000} 的结果会返回一个表示无穷大的inf。如果在这些超大值之间进行除法运算,结果会出现“不确定”的情况。
计算机处理“数”时,数值必须在4字节或8字节的有限数据宽度内。这意味着数存在有效位数,也就是说,可以表示的数值范围是有限的。因此,会出现超大值无法表示的问题。这个问题称为溢出,在进行计算机的运算时必须(常常)注意。
数学原理
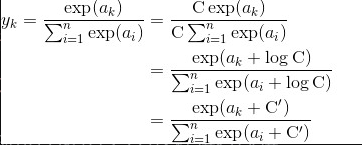
首先,在上式中分子和分母上都乘上C这个任意的常数(因为同时对分母和分子乘以相同的常数,所以计算结果不变)。然后,把这个C移动到指数函数(exp)中,记为log C。最后,把log C替换为另一个符号C'。所以,在进行softmax的指数函数的运算时,加上(或者减去)某个常数并不会改变运算的结果。这里的C'可以使用任何值,但是为了防止溢出,一般会使用输入信号中的最大值。
python 代码
def softmax(a):c = np.max(a)exp_a = np.exp(a - c) # 溢出对策sum_exp_a = np.sum(exp_a)y = exp_a / sum_exp_areturn y