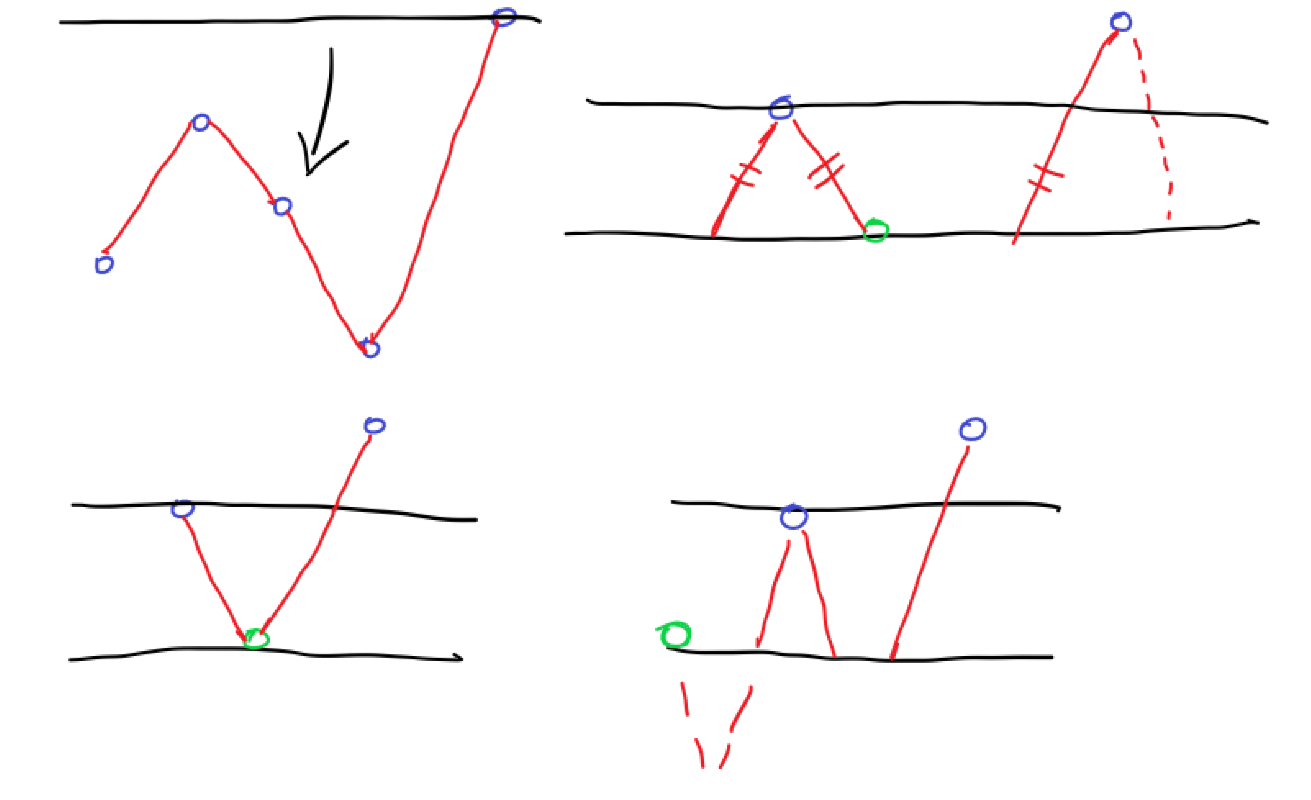
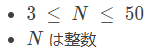A. Channel
题意: 最开始网上有 \(a\) 个人,共 \(q\) 次改变,每一次有一个人加入或离开。总共 \(n\) 个人,求这 \(n\) 个人是否都上过网,有没上过网的,都有可能。
思路:
贪心地每次选取尽可能多和少的人即可。
提交记录
B. Split Sort
题意: 给定一个排列,每次可以选取一个数 \(x\),将排列划分成小于 \(x\) 部分组成的子序列和大于等于 \(x\) 部分组成的子序列。求最少多少次操作排列会变成 \(1 \sim n\)。
思路:
如果 \(i\) 在 \(i+1\) 后面则必须有一次操作 \(x = i + 1\),显然这也是充分的。
提交记录
C. MEX Repetition
题意: 给定一个 \(n\) 长度序列 \(a_1 \sim a_n\) 两两不同且都在 \([0, n]\),一次操作是按照 \(i = 1 \sim n\) 的顺序每次让 \(a_i = \text{MEX}(a_1, a_2, \dots, a_n)\),求 \(k\) 此操作后的序列。
思路:
最重要的是读题,我们注意到恰好一个数没有被使用,这意味着第一次操作第一个数会变成这个数,第二个数变成第一个数。
所以实际上就是在数组前面加上这个数然后求一个循环位移。
提交记录
D. Two-Colored Dominoes
题意: 一个 \(n \times m\) 的棋盘上面有一些多米诺骨牌,现在将每一个牌的两个格子染成黑色和白色,要求每一列和每一行黑格子白格子数量相等。构造方案或判断无解。
思路:
首先我们发现竖着的对列没有影响,所以实际上就是要求每一列只考虑横着的有偶数个,行同理。
所以判断加构造即可。
提交记录
E. Speedrun
题意: 现在有 \(n\) 个任务,第 \(i\) 个任务需要在某一天第 \(h_i\) 小时完成,一天有 \(k\) 个小时,还有 \(m\) 对限制(不构成环),要求 \(a_i\) 在 \(b_i\) 之前完成。
现在求最后一个任务完成时间减去第一个任务完成时间的最小值。
\(n,m \le 2 \times 10^5, k \le 10^9\)。
思路:
显然如果确定第一个任务是什么就能拓扑排序求出最后任务的最早时间。
但是样例提示我们所有入度为 0 的点不一定就是最小的开始。
我们观察发现应该是一个前缀错后一天,我们考虑其会造成什么影响。
如果一个点出发能到终点且是最长路,那么如果这个点错后一天就会导致终点的答案错后一天。
于是我们倒着求一遍得出每个点能到达的最长路的终点,这样就可以枚举判断了。
提交记录
G. Swaps
题意: 给定序列 \(a_1, a_2, \dots, a_n\),一次操作定义为交换 \(a_i, a_{a_i}\)。求进行任意次操作后的所有可能的序列个数,对 \(10^9 + 7\) 取模。
\(n \le 10^6, 1 \le a_i \le n\)。
思路:
最后一题永远是作业,而且都是被我看过一遍然后鸽了的题
转化成基环树,让 \(i \to a_i\) 连边。
现在操作变成 \(a \to b \to c\) 变成 \(a \to c, b \to b\),这里要求 \(b \not = c\)。也就是如果是自环就不能操作。
显然一次操作中间的点变成自环,可以看成删去了这个点。
现在我们考虑如何计数,由于是在基环树上,我们可以先把每个环上的点的对应子树计算出来。
不妨设 \(f(i,0/1)\) 表示 \(i\) 的子树内,\(i\) 是否被删去,我们不难得出转移:
设 \(i\) 的儿子个数是 \(sz_i\),则其实 \(f(i,1) = sz_if(i,0)\)。
不难发现二者成对出现,记 \(f(i) = f(i, 0) + f(i, 1)\) 我们加起来就会得到 \(f(i) = (sz_i+1)\prod_uf(u)\)。
现在不妨考虑环上的问题,我们还是进行一个 dp,不妨设 \(g(i,0/1)\) 表示考虑到环上第 \(i\) 个点,是否被删去,设 \(c_i\) 表示环上的第 \(i\) 个点,转移如下:
同理,加起来就能得到:
但是这样会导致可能一个点转了一圈把自己也删了,所以我们需要减去这种情况,方案数为:
考虑到 \(f(c_i) = (sz_{c_i} + 1)f(c_i, 0)\),所以如果设 \(T = \prod_i f(c_i, 0)\),贡献就是 \(\sum_i (sz_i + 1)T\)。
这样就可以在 \(O(n)\) 时间解决这个问题。
官方题解的组合意义是考虑打标记,有点人类智慧。
提交记录