本篇文章介绍 \(\tilde O(n^{2.032})\) 的无向无权图全源最短路 stretch 2 近似算法和 \(\tilde O(n^{\frac 94})\) 的组合算法,以及 \(\tilde O(n^{2.214} (1 / \epsilon)^{O(1)} \log W)\) 的非负整数边权 stretch \((2 + \epsilon)\) 近似算法。其中 \((1 / \epsilon)^{O(1)}\) 表示的是 \(O\left((1 / \epsilon)^{\kappa}\right)\),\(\kappa\) 是一个常数,但是精确值不方便表示(取决于 \(\omega\) 和 \(2\) 的距离)。
\(\tilde O(n^{2.032})\) 算法的过程与 \(\tilde O(n^{2.2867})\) 无权图上的 surplus 2 近似 几乎相同,仅仅有两个改动。
-
将算法中 \(\tilde O(n^{(2 + r + \omega(r)) / 2})\) 的 Row/Column Bounded-difference \((\min, +)\) 矩阵乘改为 \(\tilde O(n^{\omega(r)} / \epsilon \log W)\) 的整数权重 \((1+\epsilon)\)-近似 \((\min, +)\) 矩阵乘。之后再将 \(\epsilon\) 的影响消除。
-
将 \(\tilde O\left(n^2 d_0^{\frac 12}\right)\) 的 base case 算法——\(\tilde O\left(n^{\frac 32} m^{\frac 12}\right)\) 的 surplus 2 近似——改为 \(\tilde O\left(m\sqrt n + n^2\right)\) 的。
剩下的算法过程完全沿用。
为什么 surplus 2 的算法可以用于 stretch 2 呢?因为对于长度 \(\geq 2\) 的最短路,surplus 2 比 stretch 2 更强,而长度 \(< 2\) 的最短路是不用算的。
原算法描述如下
|
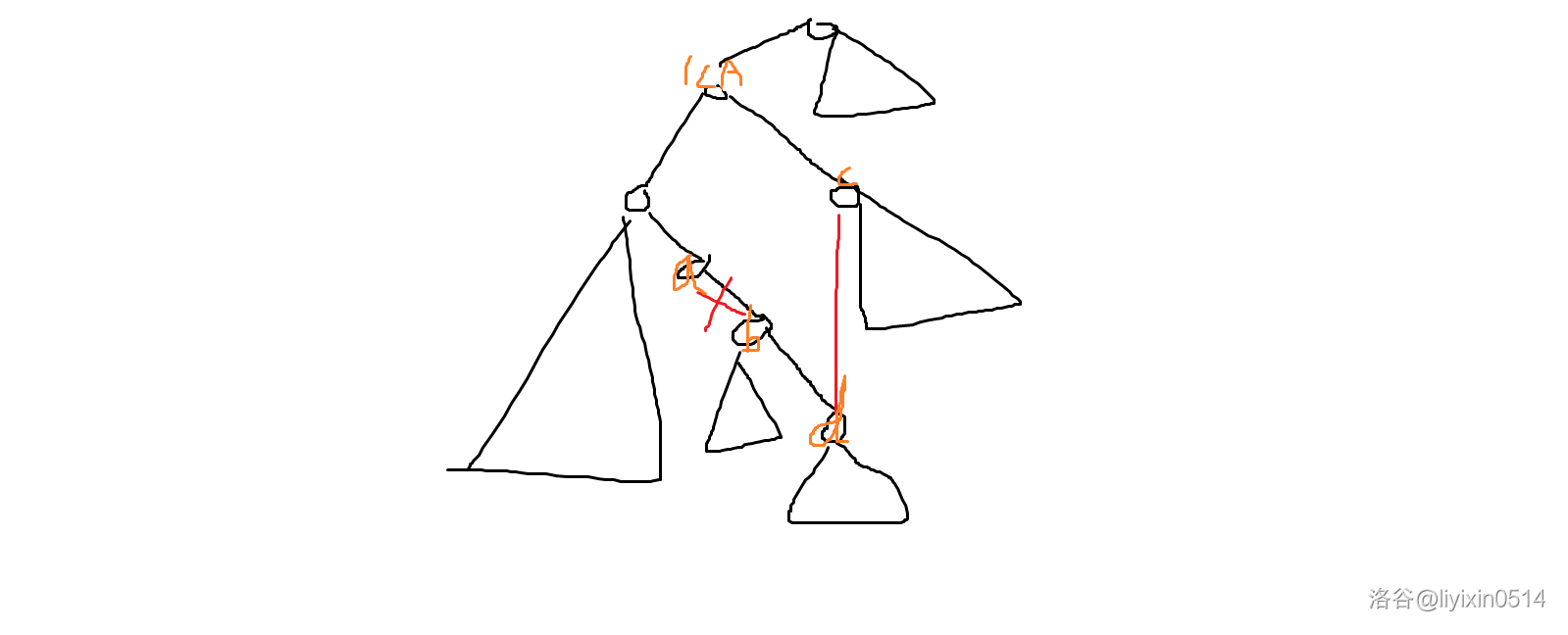
将 \(\delta(V \times D_1)\) 视作矩阵,则我们需要求出 \(\delta(V \times D_1) \star \delta(D_1 \times V)\),其中 \(\star\) 表示 \((\min, +)\) 矩阵乘法。对一般的 \((\min, +)\) 矩阵乘,没有 \(O(n^{3 - \Omega(1)})\) 的做法,但是如果我们将节点序列按照图的任意一棵生成树的欧拉序排列(此时一个点会出现多次),则 \(\delta(D_1 \times V)\) 的上下相邻两个元素的差不超过 \(1\),对于拥有这样特殊性质的 \((\min, +)\) 矩阵乘(其中一个矩阵为 Row/Column Bounded-difference),有 \(\tilde O(n^{(2 + r + \omega(r))/2})\) 的做法,其中 \(\omega(r)\) 表示 \(n \times n^r\) 矩阵和 \(n^r \times n\) 矩阵做正常矩阵乘法的指数 [Chi-Duan-Xie-Zhang '22]。
|
有两部分产生了复杂度,一部分是 base case 的 \(\tilde O(n^{\frac 52 - \frac 12 r})\),另一部分是 \((\min, +)\) 矩阵乘 \(\tilde O(n^{(2 + r + \omega(r)) / 2})\)。
现在,在 stretch 2 中,我们可以将第一部分改为 \(\tilde O(n^{\frac 52 - r})\),第二部分改为 \(\tilde O(n^{\omega(r)})\),这样便得到了 \(\tilde O(n^{2.032})\)。
当我们得到了一个 \(\tilde O(n^{\omega} / \epsilon)\) 的 \((1 + \epsilon)\) 近似的 \((\min, +)\) 矩阵乘算法时,我们可以令 \(\epsilon = 1 / \log n\),这样复杂度为 \(\tilde O(n^{\omega})\),近似比为 \(2 + 1 / \log n\)。当 \(\delta(u, v) < \log n\) 时,因为要向下取整,这是一个 \(2\) 近似,当 \(\delta(u, v) \geq \log n\) 时,我们可以用 \(\tilde O(n^2)\) surplus \(\log n\) 的做法。
这个做法相当简单,我们原先的 \(\tilde O(n^{7/3})\) surplus \(2\) 的算法中会用 BFS 计算每一层的 \(\delta(D_i \times V)\),时间复杂度为 \(O(m |D_i|)\),但现在我们不再每次重新计算,而是直接复用上一轮的结果,这样每一轮的误差会累积。对 surplus \(2(k-1)\) 近似我们可以分 \(k\) 层。
|
算法 1 (无权图上的 \(\tilde O(n^{2 - 1 / k}m^{1/k})\) surplus \(2(k - 1)\) 近似) 对图 \((V, E)\),令
从 \(1\) 到 \(k\) 枚举 \(i\),对每个 \(w' \in D_i\),在 \((V, E_{i - 1} \cup E^* \cup d_{i - 1}(\{w'\} \times V))\) 上跑 Dijkstra。 考虑将 \(d_k(u, v)\) 作为答案。 使用归纳法。使用类似 \(\tilde O(n^{7/3})\) surplus \(2\) 算法的推导可知,最短路上存在 \(w\),使得 \((w, w') \in E^*, w' \in D_{i - 1}\),因此 \(u \to w'\) 可以通过 \(d_{i - 1}\) 到达,\(w' \to w \to v\) 可以通过 \(E^* \cup E_{i - 1}\) 到达。当 \(d_{i - 1}\) 的误差为 \(e\) 时,\(d_i\) 的误差为 \(e + 2\)。 由于 \(D_k = V\),所有 \(d_k(u, v)\) 的误差都不会超过 \(2(k - 1)\)。因此这是一个 surplus \(2(k - 1)\) 近似。 复杂度为 \(\tilde O\left(\frac n{d_1} \cdot m + \sum_{i=2}^k \frac n{d_i} (nd_{i - 1} + n)\right) = \tilde O\left(kn^2 (m / n)^{1 / k}\right) = \tilde O(n^{2 - 1/k}m^{1/k})\)。 |
我们在原算法的 \(\log n\) 层每一层都运行一遍 \(1 + \frac 1{\log n}\) 近似 \((\min, +)\) 矩阵乘,最后运行一遍 \(\tilde O(n^2)\) surplus \(\log n\) 近似,将两个结果取较小值。
|
算法 2 (无向无权图上的 stretch \(2\) 近似) 对图 \((V, E)\),令
用 BFS 在 \((V, E_i \cup E^*)\) 上计算 \(\delta_i(D_{i-1} \times V)\),\(1 \leq i \leq k\),时间复杂度为 \(\tilde O\left(\frac{n^2d_i}{d_{i-1}}\right)\)。 对 \((V, E_0)\) 应用 stretch \(2\) 算法得到 \(d'(u, v)\)。时间复杂度 \(\tilde O\left(n^{3/2}d_0\right)\)。 对 \((V, E)\) 应用 surplus \(\log n\) 算法得到 \(d''(u, v)\),时间复杂度 \(\tilde O(n^2)\)。 求出 \(\min\limits_{\substack{w' \in D_i \\ 1 \leq i \leq k}}\{\delta_i(u, w') + \delta_i(w', v)\}\) 的近似值,假设 \(d\) 的选取足够分散,使得 \(k = o(n^\varepsilon)\),则复杂度为 \[\tilde O\left(n^{(2+(1 - \log_n d_0)+\omega(1 - \log_n d_0))/2}\right)
\] 考虑将 \(d(u, v) = \min\left(d'(u, v), d''(u, v), \min\limits_{\substack{w' \in D_i \\ 1 \leq i \leq k}}\{\delta_i(u, w') + \delta_i(w', v)\}\right)\) 作为答案。 使用类似上文的推导可知这是一个 stretch \(2\) 近似。 时间复杂度为 \[\tilde O\left(n^{3/2}d_0 + n^2\left(\frac{d_1}{d_0} + \frac{d_2}{d_1} + \ldots + \frac{d_{k-1}}{d_{k-2}} + \frac n{d_{k-1}}\right) + n^{\omega(1 - \log_n d_0)}\right)
\] 可知 \(\frac{d_i}{d_{i-1}}\) 都相等,令他们均为 \(2\),则 \(k = O(\log n)\),符合要求。剩下的便是解方程,令 \(d_0 = n^{1 - r}\),则方程为 \(\frac 52 - r = \omega(r)\),查表可以估计出 \(r \approx 0.4682\),最终复杂度 \(\tilde O(n^{2.032})\)。 |
如果我们想要一个组合算法,即不使用快速矩阵乘法的做法,那就是把 \(\tilde O(n^{\omega(r)})\) 改为 \(\tilde O(n^{2 + r})\),也即使用暴力矩阵乘。这样得到的式子为 \(\frac 52 - r = 2 + r\),最终复杂度为 \(\tilde O(n^{9/4})\)。这相当于只应用了来自 \(\tilde O(m \sqrt n)\) 算法的加速。
对于 \((2 + \epsilon)\) 近似,我们沿用 \(\tilde O(m \sqrt n)\) 的 \(2\) 近似算法。不过把 \(s \in S_i\) 上的 Dijkstra 改为对 \(\delta(S_i \times V)\) 的 \((1 + \epsilon)\) 近似,这称为多源最短路 (Multi-Source Shortest Path) 近似.
\((1 + \epsilon)\) MSSP 近似的做法和 \((1 + \epsilon)\) 的 APSP 近似非常接近,因为 \(\omega(r, 1, 1) = \omega(1, r, 1)\)。唯一不同的一点在于,当我们计算 \(A_{S \times V} \times A_{V \times V}^i\)(\(A_{X \times Y}\) 为集合 \(X\) 到 \(Y\) 的邻接矩阵) 时,我们不能使用快速幂计算 \(A_{V \times V}^{2^i}\),而是只能每次 \((A_{S \times V} \times A_{V \times V}^{i - 1}) \times A_{V \times V}\),因此复杂度会多一个 \(n\),这是我们不想要的。
有一类问题指出我们可以在原图上加少量的边使得所有 \((u, v)\) 都可以经过一条长度不超过 \(\beta\) 的路,使得其权值不超过 \((1 + \epsilon)\) 倍的最短路。称这样的边集为 hopset。
定理 对任意带权无向图 \(G = (V, E)\),\(\kappa > 1\),存在一个时间复杂度为 \(\tilde O(m n^{1 / \kappa})\) 算法计算 \((1 + \epsilon, \beta)\)-hopset \(H\),使得 \(\beta = \left(\frac \kappa \epsilon\right)^{O(\kappa)}, |H| = O(n^{1 + 1 / \kappa})\)。
我们令每次矩阵乘法的分辨率 \(R = \beta / \ln(1 + \epsilon)\),这样最终的近似比可以达到 \((1 + \epsilon)\)。复杂度为 \(\tilde O(n^{\omega(r)} (\kappa / \epsilon)^{O(\kappa)}\log W + mn^{1 / \kappa})\)。
如果 \(\omega(r) = 2\),\(\epsilon\) 是固定的常数,我们可以对不同的 \(n\) 选择不同的 \(\kappa\),让 \(\beta = \tilde O(1)\),比如 \(\log \log n / \log \log \log n\),这样 \(\kappa^\kappa \leq \log n\),复杂度为 \(\tilde O(n^2 \log W (1 / \epsilon)^{O(\log \log n / \log \log \log n)})\)。
否则,我们可以选择足够大的常数 \(\kappa\),使得 \(O(mn^{1 / \kappa}) \leq O(n^{\omega(r)})\),此时复杂度为 \(\tilde O(n^{\omega(r)}(1 / \epsilon)^{O(1)} \log W)\)。
分两种情况讨论是因为我们也不知道是否有 \(\omega = 2\),而对于后一种情况,为了保证复杂度是 \(n^{\omega(r)}\) 级别的,\(\omega(r)\) 越小时 \(\kappa\) 越大,\(\omega = 2\) 时我们没有办法做到 \(\tilde O(n^2(1 / \epsilon)^{O(1)} \log W)\)。
就现在而言,我们假设 \(\omega \neq 2\)。这样,在 APSP \((2 + \epsilon)\) 近似中,当 \(|S| = n^r\) 时,计算 \(S, \operatorname{ball}\)、枚举 \(y\) 的复杂度为 \(\tilde O(mn^{1 - r}) = \tilde O(n^{3 - r})\),运行 \(S_k\) 的复杂度为 \(\tilde O(n^{\omega(r)} (1 / \epsilon)^{O(1)} \log W)\)。平衡后的复杂度为 \(\tilde O(n^{2.214} (1 / \epsilon)^{O(1)} \log W)\)。