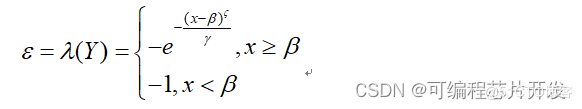逻辑回归模型

  核心：线性回归+sigmoid映射。

一、概述

  逻辑回归模型(Logistic Regression，LR)，由名称上来看，似乎是一个专门用于解决回归问题的模型，事实上，该模型更多地用于解决分类问题，尤其是二分类问题。这并不矛盾，因为逻辑回归直接输出的是一个连续值，我们将其按值的大小进行切分，不足一定范围的作为一个类别，超过一定范围的作为一个类别，这样就实现了对分类问题的解决。概况来说就是，先对数据以线性回归进行拟合，输出值以Sigmoid函数进行映射，映射到0和1之间，最后将S曲线切分上下两个区间作为类别区分的依据。

二、算法原理

  算法核心是线性回归+sigmoid映射。具体来说，就是对于一个待测样本，以指定的权重和偏置量，计算得到一个输出值，进而将该输出值经过sigmoid进一步计算，映射至0和1之间，大于0.5的作为正类，不足0.5的作为负类。模型原理图示可概括为

  线性回归的表达式可表示为 \(z=w\cdot x+b\)，sigmoid函数表达式表示为 \(y=\frac{1}{1+e^{-z}}\)，那么逻辑回归模型的表达式即是\(y=\frac{1}{1+e^{-(w\cdot x+b)}}\)。
逻辑回归的分类算法可表示为

\[\left\{ \begin{aligned} &-1, \frac{1}{1+e^{-(w\cdot x+b)}}<0.5\\ &1, \frac{1}{1+e^{-(w\cdot x+b)}}\geq0.5 \end{aligned} \right. \]

  逻辑回归模型的训练采用交叉熵损失函数，在优化过程中，计算得到最佳的参数值，表达式如下

\[J\left( \theta \right)=-\frac{1}{m} \sum_{i=1}^{m}\left[ {y^ilog(h(x^i))} +(1-y^i)log(1-h(x^i))\right] \]

三、Python实现

import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn import metrics
## 1.定义数据集
train_x = [[4.8,3,1.4,0.3],[5.1,3.8,1.6,0.2],[4.6,3.2,1.4,0.2],[5.3,3.7,1.5,0.2],[5,3.3,1.4,0.2],[7,3.2,4.7,1.4],[6.4,3.2,4.5,1.5],[6.9,3.1,4.9,1.5],[5.5,2.3,4,1.3],[6.5,2.8,4.6,1.5]
]# 训练数据标签
train_y = ['A','A','A','A','A','B','B','B','B','B'
]# 测试数据
test_x = [[3.1,3.5,1.4,0.2],[4.9,3,1.4,0.2],[5.1,2.5,3,1.1],[6.2,3.6,3.4,1.3]
]# 测试数据标签
test_y = ['A','A','B','B'
]train_x = np.array(train_x)
train_y = np.array(train_y)
test_x = np.array(test_x)
test_y = np.array(test_y)## 2.模型训练
clf_lr = LogisticRegression()
rclf_lr = clf_lr.fit(train_x, train_y)## 3.数据计算
pre_y = rclf_lr.predict(test_x)
accuracy = metrics.accuracy_score(test_y,pre_y)print('预测结果为：',pre_y)
print('准确率为：',accuracy)

End.

pdf下载