\(1.\) 定义和性质
\(\textbf{定义 1 } \text{(分拆)}\)
定义整数 \(n\) 的一个拆分为 \(\lambda = (\lambda_1, \lambda_2, \dots, \lambda_m)\),满足 \(\forall i, \lambda_i \ge \lambda_{i + 1}\),且 \(\lambda_i\) 的加和为 \(n\)。记其为 \(\lambda \vdash n\),并令 \(\lvert \lambda \rvert = n\),\(\ell (\lambda) = m\)。
对分拆和有基础限制分拆的计数不再展开,可以由生成函数直接推导得到结果。
杨表的组合结构可能来自于这样一个有趣的问题:有一个直角形状、大小无限的桶,现在要向其中放入 \(n\) 个大小相同的球,形成一个稳定的形状。那么,有多少种放球的方案呢?
一种依次放入五个球的例子如下:

我们该如何将这样的方案抽象成组合结构呢?分拆为我们提供了一种方法——
\(\textbf{定义 2 } \text{(杨图)}\)
对一个拆分 \(\lambda \vdash n\),形状为 \(\lambda\) 的杨图(Young diagram)为一个 \(\ell (\lambda)\) 行、第 \(i\) 行由 \(\lambda_i\) 个单位方格排列而成的表格,每行的方格左对齐,记作 \([\lambda]\)。称 \([\lambda]\) 的高度为 \(\ell(\lambda)\)。
若将单位方格换为单位点,其便被称为 Ferrers 图。
有三种画杨图的方式:英式,短行在下;法式,长行在下;俄式,直角在下。一般采用英式画法(虽然 tableau 是法文)。
若对 \(\lambda \vdash n\) 和 \(\mu \vdash n\),有 \(\ell (\lambda) \ge \ell (\mu)\),且 \(\forall i, \lambda_i \ge \mu_i\),那么我们称 \(\lambda\) 包含 \(\mu\)。容易看出这包含关系是分拆集合上的一个偏序关系。
杨图中每个单位方格的位置可以唯一地用其所在行和列表示。若我们将行按照方格数由大到小、列按照由左向右标号(由 \(1\) 开始),那么一个杨图 \([\lambda]\) 可以被表示为集合 \(\{(i, j)\mid 1\le i\le \ell(\lambda), 1\le j\le \lambda_i\}\)。这样若 \(\lambda\) 包含 \(\mu\),有 \([\mu] \subseteq [\lambda]\)。
对这种集合表示方法,我们也可以推广一下,用 \(\mathbb Z^2\) 的子集来表示一个图(diagram)。这里的横坐标表示行数,其由上到下递增;纵坐标表示列数,其由左到右递增。按四联通的方式建图,我们也可以自然地定义图论相关性质。
一个拆分 \(\lambda \vdash n\) 也可以被描述为无穷序列 \((\lambda_1, \lambda_2, \dots)\),只需要令 \(\forall i > \ell (\lambda), \lambda_i = 0\)。定义 \(\lambda\) 的共轭(或转置)分拆为 \(\lambda' \text{ s.t. } \forall \lambda'_k = \left\lvert \left\{ i > 0 \mid \lambda_i \ge k\right\} \right\rvert\)。若把这过程放在图形上,那么 \([\lambda]\) 到 \([\lambda']\) 就是沿主对角线作对称,或行列互换。
\(\textbf{定义 3 } \text{(杨表)}\)
对一个形状为 \(\lambda \vdash n\) 的杨图 \([\lambda]\),若将 \(1\sim n\) 这 \(n\) 个正整数填入每个单位方格,使得每一行从左到右、每一列从上到下的数字都严格递增,就得到了一个形状为 \(\lambda\) 或 \([\lambda]\) 的(标准,standard)杨表(Young tableau)。容易知道,正整数集可以被替换为任意具有全序的集合,这时的杨表被称作近似(near)杨表。普通杨表也是近似杨表。
若这 \(n\) 个正整数可以被重复填入,那么就会存在非严格递增的情况。若每一行从左到右的数字非严格递增,但每一列从上到下的数字严格递增,就得到了半标准(semistandard)杨表。
对一个形状为 \(\lambda \vdash n\) 的杨表,其权重为 \((c_1, c_2, \dots, c_n)\),其中 \(c_i\) 表示 \(i\) 在杨表中出现的次数。容易知道标准杨表的权重必定为 \((1, 1, \dots, 1)\)。
记杨表 \(P\) 的形状为 \(\text{sh}(P)\),其既可以是拆分,也可以是杨图。
对杨图 \(D\),令 \(\text{SYT}(D)\) 为形状为 \(D\) 的标准杨表,并令 \(f^D = \lvert \text{SYT}(D) \rvert\)。对拆分 \(\lambda\) 类似地定义上述记号。注意到若 \(\lambda\) 的转置为 \(\lambda'\),则 \(f^\lambda = f^{\lambda'}\)。例如: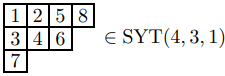
\(\textbf{定义 3 } \text{(斜)}\)
对两个拆分 \(\lambda, \mu\),若 \([\mu] \subseteq [\lambda]\),那么形状为 \(\lambda / \mu\) 的斜(skew)杨图 \([\lambda / \mu]\) 由集合差 \([\lambda] / [\mu]\) 定义,即集合 \(\{(i, j) \in [\lambda]\mid \mu_i + 1\le j\le \lambda_i\}\) 对应的图。
例如: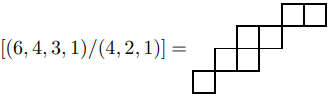
下文中的“杨表”指代标准杨表。
\(2.\) 确定杨图,对杨表的计数
\(\textbf{定理 1 } \text{(钩长公式)}\)
对任意拆分 \(\lambda\),以及其中的一个方格 \(c = (i, j) \in [\lambda]\),定义其钩(hook)为
\[H_c = [\lambda] \cap \left(\{(i, j)\} \cup \{(i, j’) \mid j' > j\} \cup \{(i', j) \mid i' > i\} \right) \]即 \(c\) 及其正右方、正下方的格子。记 \(\lambda'\) 为 \(\lambda\) 的共轭,其钩长(hook length)为 \(h_c = \lvert H_c \rvert = \lambda_i + \lambda'_j - i- j + 1\)。那么有钩长公式(hook length formula)
\[f^\lambda = \frac{\left\lvert \lambda \right\rvert !}{\prod_{c\in [\lambda]} h_c} \]
证明:我们将使用一个概率论的方法\({}^{[4]}\)。
取自然数列 \((\lambda_1, \lambda_2, \dots)\)。若 \(\lambda \vdash n\),则令 \(F(\lambda_1, \lambda_2, \dots)\) 为定理 \(1\) 中的 RHS,反之令其为 \(0\)。考虑 LHS 的组合意义,我们需要递推,每次加入一个元素。考虑元素 \(n\)。由于 \(n\) 大于当前杨表中任意其他元素,其必定在某行/列的末尾位置(角落,钩长为 \(1\))。因此不妨令 \(n\) 位于第 \(\alpha\) 行,我们要证明的就是
简记为
注意上式确实枚举了所有的角落,这是由于若 \(\alpha\) 行不出现角落,那么 \(\lambda_{\alpha + 1} = \lambda_\alpha\),从而 \(\lambda_{\alpha + 1} > \lambda_\alpha - 1\) 使得这样的 \(F_\alpha = 0\)。
我们为什么要这样定义呢?这是由于,通过每次加入 \(n\),我们可以得到所有的杨表,因此上式所拥有的结构的组合意义符合杨表的组合意义。我们只需要证明上式成立,也就是 RHS 具有和 \(f^\lambda\) 同样的组合形式,这也就证明了原式的等号。整理得到,我们要证明的就是
考察一个基于杨图的随机过程,我们维护一个指针,并进行如下的操作:
- 初始,随机选择一个格子指向它;
- 在这个格子的钩中选一个格子,将指针指向它,随后检查当前位置;
- 若指针指向的格子在角落,结束这一过程;
- 反之,执行 \(2.\) 操作。
设这一过程结束于角落 \((\alpha, \beta)\) 的概率为 \(p(\alpha, \beta)\)。显然有 \(\sum_{\alpha} p(\alpha, \beta) = 1\)。因此,我们只需要证明
令 \(p(A, B\mid a_1, b_1)\) 为该过程起始于 \((a_1, b_1)\),终结于 \((\alpha, \beta)\),路径上经过的横坐标组成集合 \(A = \{a_1, a_2, \dots\}\),纵坐标组成集合 \(B = \{b_1, b_2, \dots\}\) 的概率。考虑第一步是水平方向还是竖直方向,可以得到
使用归纳法,我们要证明
这是由于 \(p(A / \{a_1\}, B \mid a_2, b_1) = (h_{(a_1, \beta)} - 1) \text{RHS}\),\(p(A, B / \{b_1\}\mid a_1, b_2) = (h_{(\alpha, b_1)} - 1) \text{RHS}\)。但由于 \(h_{(a_1, b_1)} + 1 = h_{(a_1, \beta)} + h_{(\alpha, b_1)}\),知道
首先随机选择起始点 \((a, b)\),并令 \(A \subseteq \{1, \dots, \alpha\}, B \subseteq \{1, \dots, \beta\}\) 有 \(a = \min A, b = \min B\),我们有
化简即可。\(\square\)
例如,\((1, 2)\) 的钩形如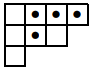
\(\textbf{定理 2 } \text{(F. G. Frobenius, 1900)}\)
对拆分 \(\lambda\),令 \(l_i = \lambda_i + \ell (\lambda) - i\),那么
\[f^\lambda = \frac{\lvert \lambda\rvert !}{\prod_{i = 1}^{\ell (\lambda)} l_i !} \prod_{i < j} (l_i - l_j) \]
证明:等价于定理 \(1\)。\(\square\)
\(3.\) RSK 算法
虽然这是一个算法,但它实际上指出了一个排列与杨表对的双射。RSK 分别是 G. de B. Robinson, C. Schensted 和 D. E. Knuth。是你,高德纳!
下面我们将构造一个双射,从而证明
令 \(\pi\) 对应的杨表对为 \((P_\pi, Q_\pi)\)。
RHS 的组合意义是经典的:长度为 \(n\) 的排列的数目,即 \(\lvert\mathcal S_n\rvert\),但右侧该怎么得到呢?这就是 RSK 算法的核心思路:维护两个杨表,构造依排列顺序插入元素的操作,并通过一些限制使得其形状保持相同。
既然依排列顺序,那么我们就不能保证插入过程中维护的是杨表,而只能保证这是一个近似杨表。假设我们有一个近似杨表 \(P\),记 \(P\leftarrow k\) 为将 \(k\) 自第一行插入 \(P\) 的操作,称其为一次行插入。需要执行如下的程序:
- 执行过程中,维护当前行变量 \(c\) 与当前值变量 \(k\),\(c\) 初始化为 \(1\),\(k\) 初始化为要插入的值。
- 寻找最小的 \(r\) 使得 \(P_{(c, r)} > k\)。
- 若不存在这样的 \(r\),那么将 \(k\) 插入第 \(c\) 行的末尾定满足要求。插入后结束程序。
- 反之,交换 \(k\) 与 \(P_{(c, r)}\),并将 \(c\) 自增 \(1\),判断是否越界。
- 若不存在第 \(c\) 行,则新建一行,将 \(k\) 作为 \(P_{(c, 1)}\)。
- 反之,执行 \(2.\) 操作。
同样,可以定义 \(k \rightarrow P\) 为将 \(k\) 自第一列插入 \(P\) 的操作,称其为一次列插入。
下面就可以描述 RSK 算法的程序了。取排列 \(\pi \in \mathcal S_n\),我们需要构造一个近似杨表对序列 \((P_0, Q_0), (P_1, Q_1), \dots, (P_n, Q_n)\),使得 \(P_i, Q_i\) 为两个近似杨表,且均包含 \(i\) 个方格。RSK 算法需要执行如下的程序:
- 初始时,令 \((P_0, Q_0) = (\varnothing, \varnothing)\)。随后执行 \(n\) 轮如下操作。
- 第 \(i\) 轮时:
- \(P_i \leftarrow (P_{i - 1} \leftarrow \pi_i)\)
- 将 \(i\) 插入 \(Q_{i - 1}\) 得到 \(Q_i\),使得 \(P_i, Q_i\) 形状相同。(注意:此处不是行插入)
- 返回 \((P_n, Q_n)\) 作为所需的杨表对 \((P_\pi, Q_\pi)\)。
由于 \(i\) 插入的位置必定为角落,因此 \(Q_n\) 必定为杨表。
令 \(A_{n} = \{(P, Q) \mid \text{sh}(P) = \text{sh}(Q) = \lambda, \lvert \lambda \rvert = n\}\)。通过这一程序,我们自然能得到 \(\mathcal S_n \to A_n\)。反过来怎么做呢?我们可以把行插入也反过来,得到行删除。
令当前的表对为 \((P,Q)\),我们要删除 \(Q\) 中的 \(t\),只需要执行以下操作:
- 执行过程中,维护当前行变量 \(c\) 与当前值变量 \(k\),\(c\) 初始化为 \(t\) 所在行的上一行,\(k\) 初始化为 \(P\) 中 \(t\) 对应位置。
- 寻找第 \(c\) 行中比 \(k\) 大的最小元素 \(k'\),交换 \(k\) 与 \(k'\),并将 \(c\) 自减 \(1\),判断是否越界。
- 若 \(c = 0\),返回 \(k\) 作为 \(\pi_t\)。
- 反之,执行 \(2.\) 操作。
将如上的行删除倒序执行(即先删除 \(n\)),我们就得到了其对应的排列。\(\square\)
那么,我们如何计算 \(\sum_{\lambda \vdash n} f^\lambda\) 呢?仍然可以考察 RSK 算法,我们知道这时只需要 \(P = Q\),并计数对应的 \(\pi\) 即可。
注意到 \(\pi \leftrightarrow (P, Q)\) 那么 \(\pi^{-1} \leftrightarrow (Q, P)\)。这时我们知道 \(\pi = \pi^{-1}\),也就是 \(\pi^2 = 1\),对应的 \(\pi\) 即 \(n\) 阶对合,其只有大小为 \(1,2\) 的置换环。
知道了这一性质后,计数就变得简单了。令 \(\mathcal C\) 为大小为 \(1, 2\) 的置换环的有标号类,那么 \(n\) 阶对合的有标号类即为 \(\text{Set}(\mathcal C)_n\)。这就是 \([x^n] \exp (x + x^2 /2)\)。你当然可以提取这个系数,可以知道这就是
未免有点太不好看了吧?
\(4.\) 应用
首先不可不提的是 LIS(最长上升子序列)和 LDS(最长下降子序列)的刻画。
对排列 \(\pi\),知道 \(P_\pi\) 第一行的长度就是 \(\pi\) 的 LIS 长度。做过 LIS 题的都知道,只看第一行,这过程和 \(O(n\log n)\) 求 LIS 长度的方法本质相同,而这方法得到的不一定是 LIS 本身。
\(\textbf{引理 1 } \text{(C. Schensted, 1961)}\)
对一个近似杨表 \(S\) 与两个元素 \(x, y\),有
\[(x\rightarrow S) \leftarrow y = x\rightarrow (S \leftarrow y) \]
证明:繁,见 Schensted 原论文 Lemma 6。\(\square\)
根据该引理,对排列 \(\pi\),若翻转 \(\pi\) 得到 \(\mu\),那么 \(P_{\mu}\) 即为 \(P_{\pi}\) 翻转行列后的杨表。同时由于 \(\pi\) 的 LDS 就是 \(\mu\) 的 LIS,知道这值就是 \(\ell(\text{sh}(P_\pi))\)。
待补。
References:
\([1]\): yfz, 浅谈杨氏矩阵在信息学竞赛中的应用;
\([2]\): OI wiki, 杨氏矩阵;
\([3]\): Ron M. Adin et al., Enumeration of Standard Young Tableaux;
\([4]\): Curtis Greene, Albert Nijenhuis, and Herbert S. Wilf, A Probabilistic Proof of a Formula for the Number of Young Tableaux of a Given Shape.