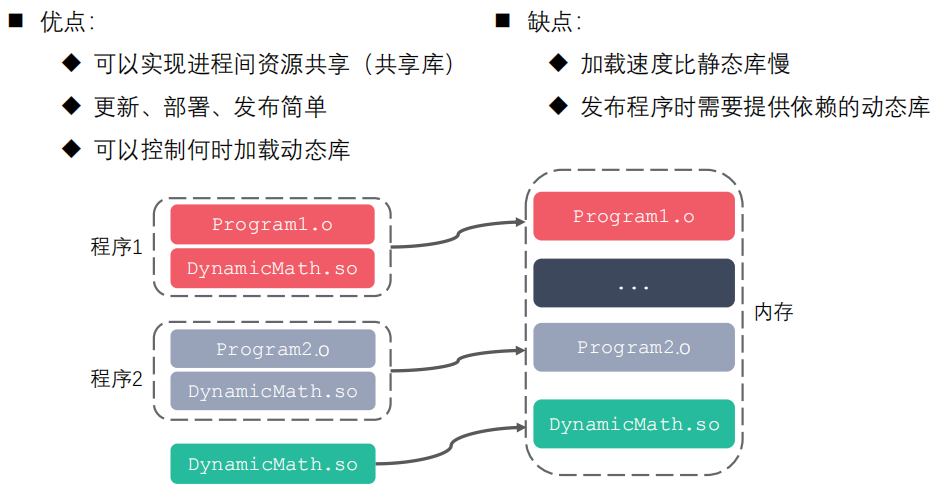
Lecture 06 Real-time Environment Mapping (Precomputed Radiance Transfer)
Shadow from environment lighting
- 通常情况下要实时渲染非常困难
- 在不同观察方向上
- As a many-light problem: Cost of Shadow Map is linearly to #light
- As a sampling problem: Visibility项V会变得非常复杂
- 对于一个shading point,不同方向上的遮挡情况可能会是截然不同的
- Visibilty项不好被拆分出来,对于glossy BRDF,BRDF是高频的,无法拆分(不满足smooth),对于Lighting,support是整个半球,也无法拆分(不满足small support)
- 工业界的解决方案
- 只生成(或者多一点)最重要/最亮的光源的Shadow Map(比如太阳)
- 相关研究
- Imperfect shadow maps(全局光照产生的阴影)
- Light cuts(离线渲染中,将反射物当作小的光源,做归类,然后近似,解决many-light问题)
- RTRT(Real-time Raytracing,思路:path tracing+denoise)
- Precomputed radiance transfer
Background Knowledge
Frequency and filtering
高频低频描述信号在空间上变化的剧烈程度
Filtering滤波,去除特定频率的信号
卷积:图形学上一般用于求平均
时域上做卷积等于频域上做乘积(原图频谱乘于卷积核频谱),时域频域通过傅里叶变换和逆傅里叶变换转换
product intergral
两个函数相乘再积分可以理解成一个卷积/滤波操作,这两个信号的频谱有任意一个是低频的,乘出来的结果就是低频的
-
任何一个操作只要满足这种性质就称作product intergral
-
Low frequency == smooth function / slow changes / etc.
-
积分结果的频率又两个函数频率最低的那个决定
Basis functions 基函数
- 将一个函数表示为若干个函数的线性组合,用于组合的函数称为基函数
- 傅里叶级数就是一系列基函数的组合
- 多项式也是一系列基函数的组合
Real-time environment lighting (& global illumination)
Spherical Harmonics (SH) 球面谐波函数/球谐函数
定义
- SH是一系列定义在球面上的二维基函数(对方向的一个函数)
- 在三维空间中,任何一个方向其实是一个二维的变量,因为这个方向可以用\(\theta\)和\(\phi\)来描述(如地球上的经纬度)
- 球面上某一个点就描述了一个独特的方向,或者认为单位球面上一个点就是一个方向
- 类似于一维情况下的傅里叶级数(常数、\(\sin\)、\(\cos\))
球谐函数的可视化

-
颜色表示值
-
对于第一层,只有一个函数,且球上任何位置的值都是一样的
如\(l=0,m=0\)的基函数,北极的值非常大,南极的值的绝对值非常大,赤道位置的值靠近0
可以看到\(l\)越大,值变化越快,也就是频率越大
-
对于第二层,有三个函数,这三个函数相当于某个半球上有一个值,另一个对称的半球上是不同的值,这三个函数各自的朝向不一样
-
对于第三层,有五个函数,这五个函数的频率是一样的,只是各自长得有些区别
-
第四层同理
Spherical Harmonic仅仅是二维的函数,并且有不同的频率,每种频率有几种不同类型的函数
-
对于第\(l\)层,有\(2l+1\)个函数,称为第\(l\)阶的SH,每一阶的SH有\(2l+1\)个基函数,编号从\(-l\)到\(l\)
-
对于前\(n\)阶,共有\(n^2\)个函数(如前三阶\(l\) 从\(0\)到\(2\),共9个函数)
为什么不用二维傅里叶变换呢?
-
因为Rendering中用到很多球面上的函数,如果展开成二维的傅里叶级数,再根据不同频率考虑它,做一些近似,得到的结果再变回球面上,很可能球面上会有一条缝
-
而Spherical Harmonics本身就定义在球面上,很适用于直接用它来分析一些球面上函数的性质
球谐函数的基函数
- 球谐函数的每一个基函数是利用勒让德多项式来写的
- 勒让德多项式本身是很复杂的多项式
- 只需要知道一个基函数长这样,可以用某些数学工具来定义它不同方向上的值是多少就可以了
- 投影
-
恢复:使用系数和基函数恢复出原函数,求出的系数不是无限的而是截断的
通常是取到\(l\)阶,前\(l\)阶的基函数都用
-
对于\(c_i=\int_{\Omega}f(\omega)B_i(\omega)d\omega\)可能无法求得解析解,需要预计算
相当于是把环境光贴图用SH转化成一系列的数据,在渲染时通过数据和SH计算出光照
Spherical Harmonics的一些性质
-
orthonormal 正交性
一个基函数投影到任意另外的基函数上,结果为0
-
simple projection/reconstruction 投影和恢复简单
只需product intergral即可
-
simple rotation
- 想要旋转原函数,相当于旋转每一个基函数相同的角度,旋转后基函数的线性组合就等于旋转后的原函数
- 这样就将旋转原函数问题转换成了旋转基函数问题,而旋转后的基函数都可以被同阶的基函数的线性组合得到
- 基函数旋转后不再是基函数(因为SH基函数固定是哪几个)
-
simple convolution
-
few basis functions: low freqs
不太适合用来表示高频函数
Prefiltered env. lighting
- Prefiltered + single query = no filtering + multiple queries
一个例子:Diffuse BRDF
Environment Lighting
在Diffuse BRDF中,环境光可以是很复杂的函数,而Diffuse BRDF是很光滑的(低频),相当于是一个低通滤波器(两个函数做product intergral时,结果频率取决于最低频的函数),于是就可以用很低阶的Spherical Harmonics来描述Diffuse环境光照
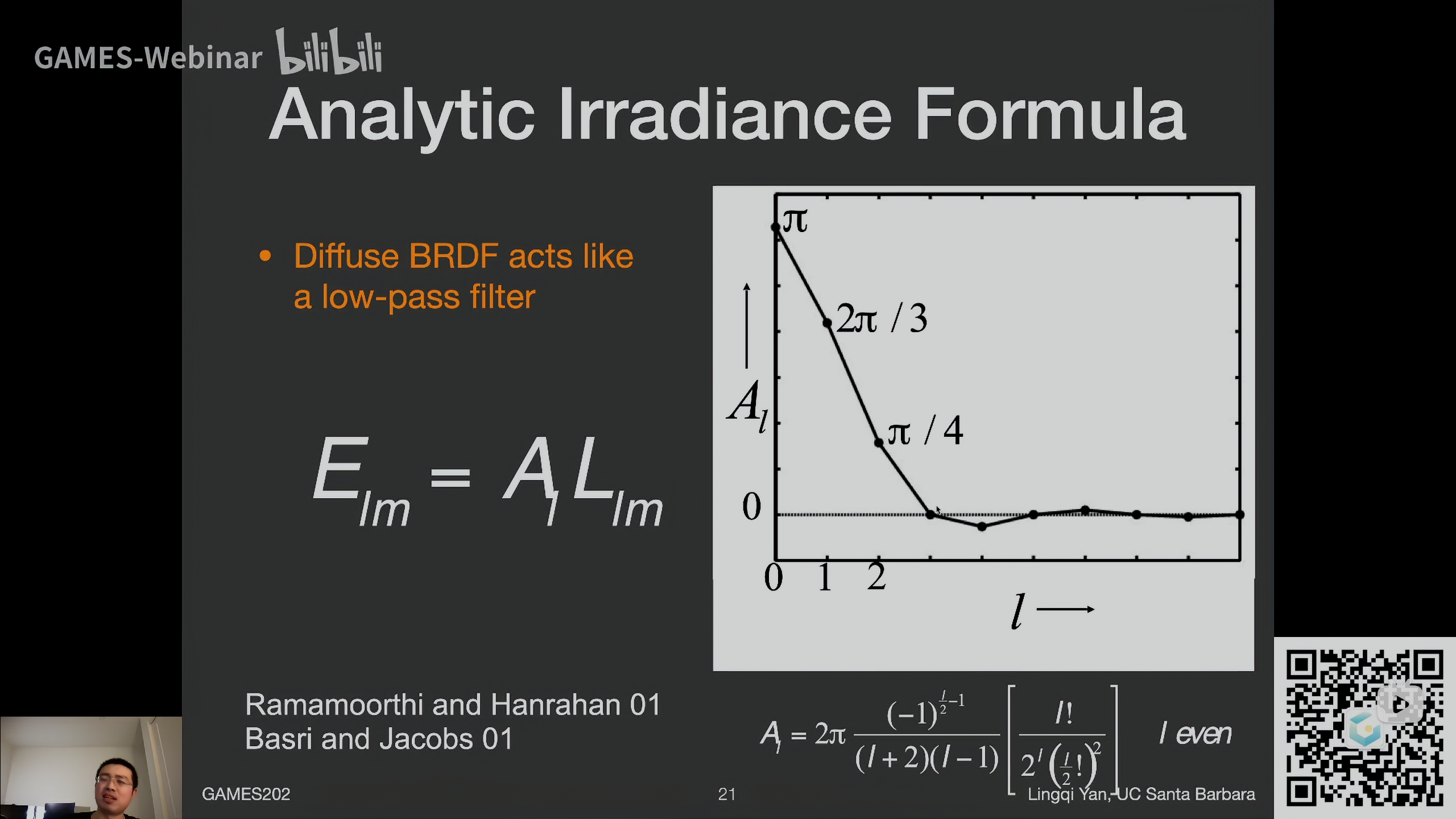
可以看到在第三阶开始函数变化几乎可以忽略
9 Parameter Approximation
既然环境光可以用非常低的频率描述,那光照也不需要高频信息了
Lighting项同样使用前三阶的SH来描述,最终结果的误差只有1%
因此对于任何Diffuse物体,都可以只用前三阶的SH来描述
Precomputed Radiance Transfer (PRT)
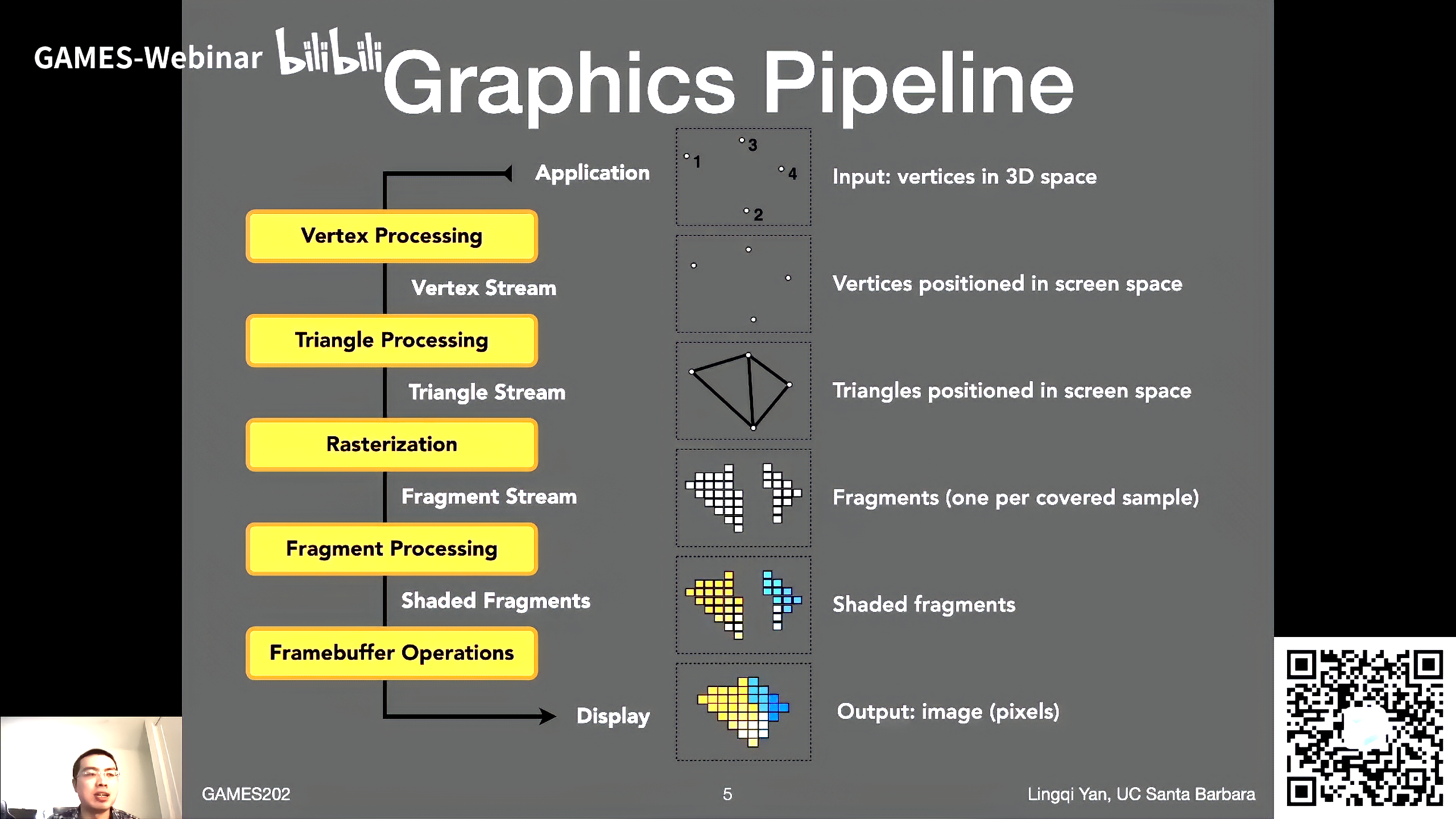
Rendering under environment lighting
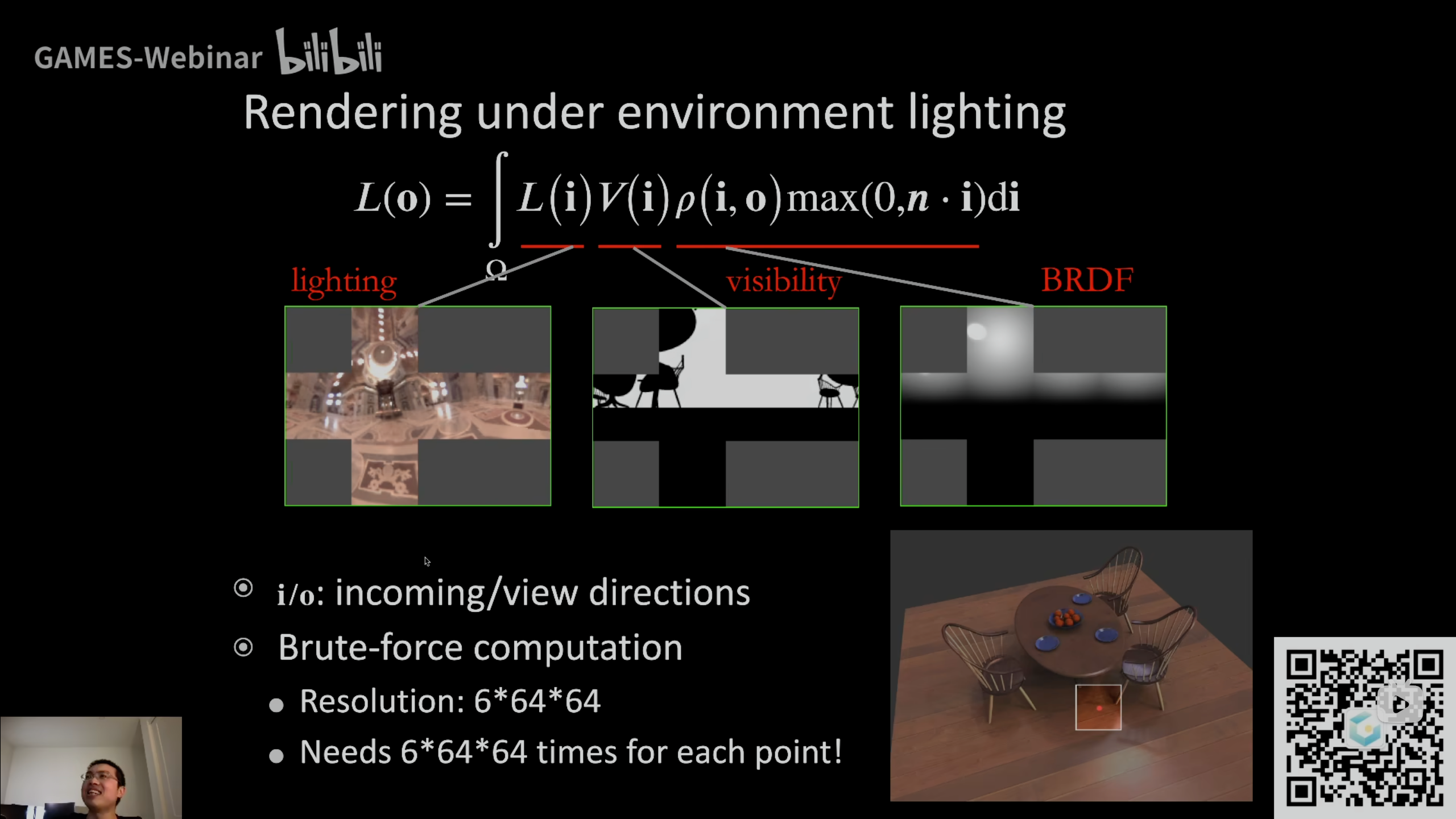
通常会把渲染方程写成Lighting项、Visibility项和BRDF项
- Lighting描述成一个球面函数
- Visibility描述成一个球面函数:一个点往四面八方看,下半球完全是黑的,上半球有物体遮挡时看不到,所以结果非0即1,也可以描述成球面函数
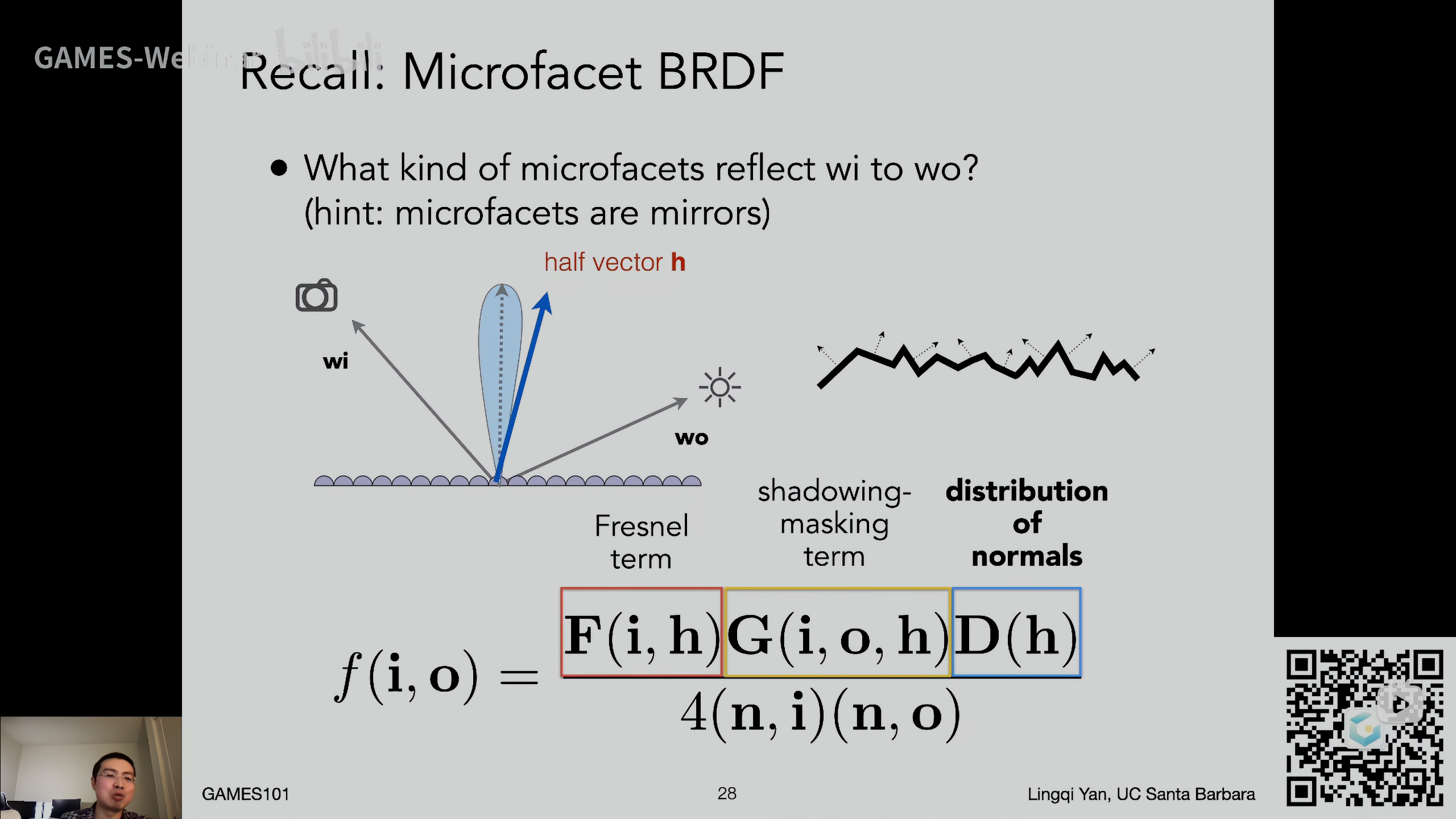
- BRDF项:BRDF是一个四维函数,两个方位角(入射方向和观察方向),每个是二维,其中已知观察方向,那么只剩入射方向的两个参数,自然可以描述成一个球面函数
如果蛮力法计算,假设Lighitng项是6面的\(64\times64\)的分辨率,那么每个shading point需要计算\(6\times64\times64\)次,无法承担
Precomputed Radiance Transfer (PRT)
基本思想
假设场景中只有光照发生改变,其他不变
- 坏处是固定了light transport,意味着场景中的物体全都不能动,否则会改变Visibility项
- 同时也固定了物体材质(BRDF项),因此物体材质也不能改变
我们已经考虑了Visibility项,所以结果是带shadow的
我们可以把Lighting作为一项,Lighting以外的作为一项 (light transport)
Lighting来自四面八方,是一个二维的球面函数,将其拆成一系列Basic function
使用基函数近似Lighting
\(L(i)\approx \sum l_iB_i(i)\)
这里认为Lighting是改变的,light transport是不变的,是shading point自己的性质,于是可以预计算light transport
这里的shading point可以是物体的顶点 (per vetex shading),也可以是pixel (per pixel shading),若选择逐顶点,后续用的就是三角形内部插值的结果了
预计算阶段
Diffuse Case
\(L(o)=\rho\underset{\Omega}{\int}L(i)V(i)max(0,n\cdot i)di\)
Diffuse情况下BRDF是一个常值,于是diffuse可以单独拿出来,公式中写作\(\rho或k_d\)
Diffuse BRDF与视角无关,所以相机是可以动的
求Visibility项的球面函数:因为是预计算,直接trace光线
\(L(i)\approx\sum l_i B_i(i)\)
于是又可以写成\(L(o)=\rho\underset{\Omega}{\int}\sum l_i B_i(i)V(i)max(0,n\cdot i)di\)
- 在数学中需要考虑能否交换积分和求和的顺序,在图形学中从不考虑
- 在Differntiable Rendering 可微分渲染中还是要考虑
交换积分和求和的顺序后:\(L(o)=\rho\sum l_i\underset{\Omega}{\int}B_i(i)V(i)max(0,n\cdot i)di\)
根据前面球谐函数提到的内容
积分得到的内容实际上就是将light transport球面函数投影到某个Basic function上的系数是多少
我们的前提是light transport是不变的,那么对于任何一个shading point都可以投影到任何一个basic function上去,只需记录得到的数即可
\(T_i\)是前一步预计算得到的数,这里求和是两个向量的逐个元素\(i\)相乘,也就是点乘,这完成了shading包括shadow的计算
那么对于相同场景的不同环境光贴图,如一张室外一张室内,只需分别预计算好,环境光贴图就对应向量\(l_i\),就可以切换光源了(只要光源被预计算过)
-
环境光预计算:将环境光转换成球面函数,那么每一点记录的就是球谐函数基函数的一组系数,也就是一个向量,所以光照变成了一个向量\(l_i\),这个向量的求法\(l_i=\underset{\Omega}{\int}L(i\cdot B_i(i)di\),恢复原函数时:\(L(i)\approx\sum l_iB_i(i)\)
-
如果光源旋转过呢,不就相当于换了一种光源,无法处理了吗?
预计算的光源投影到Spherical Harmonics上,如果发生了一些旋转,可以立刻得到旋转后对应的SH的系数是怎样变化的(旋转不变性),见前文球谐函数的性质
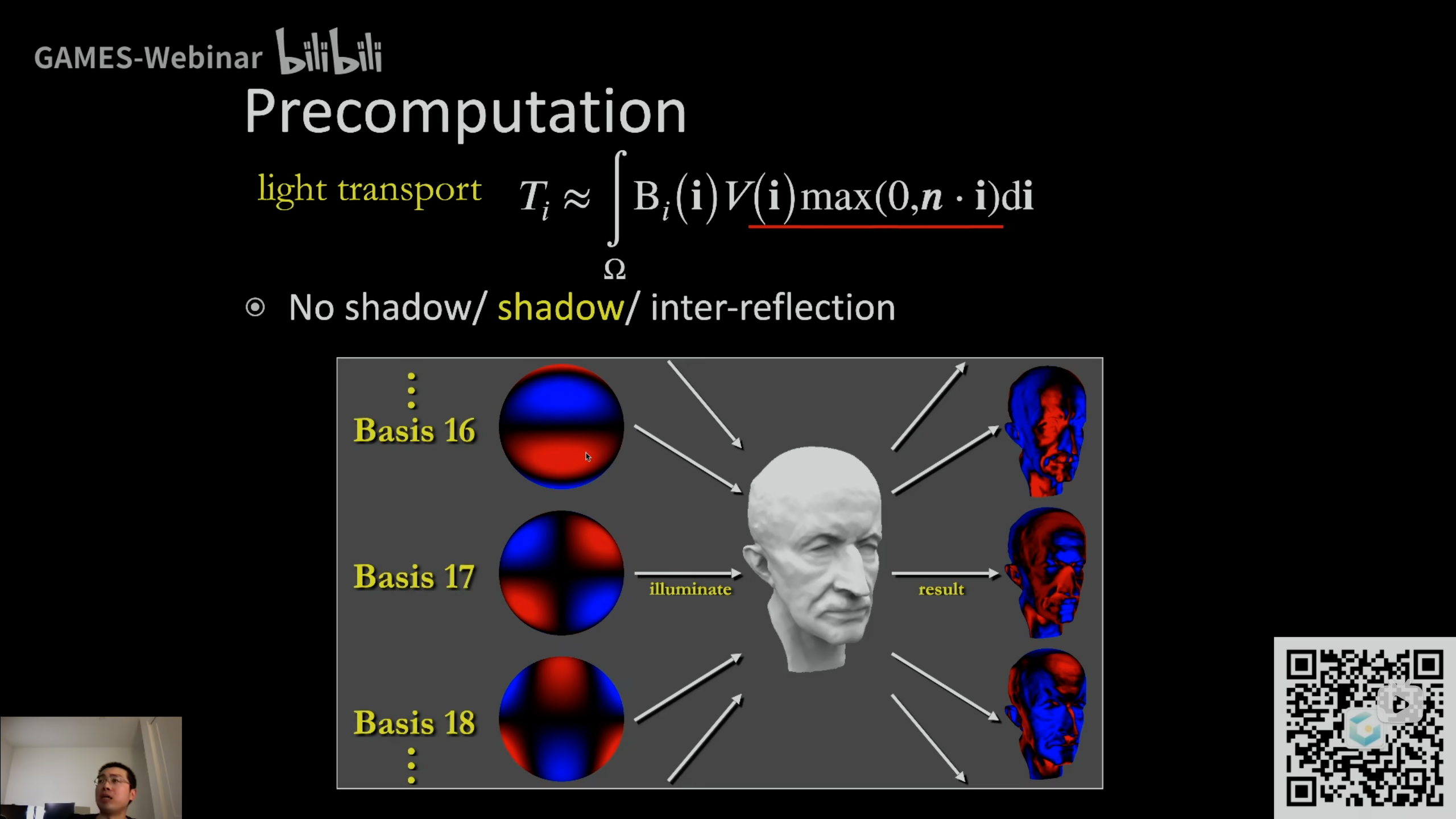
另一种理解方式:
对于每一个基函数,都计算一遍结果的环境光,图中\(T_i\approx\underset{\Omega}{\int}B_i(i)V(i)max(0,n\cdot i di)\)相当于一个渲染方程,将环境光项\(L_i\)换成了\(B_i\)
Glossy Case
对于Glossy的BRDF,结果并非常数,而是与入射方向角、出射方向角有关(各两维\(\theta\ \phi\)),所以Glossy BRDF是一个完整的四维的BRDF
而因为是环境光,所以将输入维度积分,只剩输出方向(也就是观察方向),因此\(light\ transport\)向量中的元素是\(o\)的函数\(T_i(o)\)
虽然Glossy BRDF是一个四维函数,但给定不同\(o\),\(Light\ transport\)项就只是一个二维函数了
那么继续将\(T_i\)也投影到Spherical Harmonics上,那么\(light\ transport\)项不在是一个向量,而是一个矩阵了
(给定任何一个\(o\)得到一个向量,将所有向量摆在一块是一个矩阵)
-
存储开销:
对比Diffuse情况,原本存的是向量,现在存是矩阵。对于每一个shading point如果原先用5阶SH(25个SH),在Glossy情况就需要\(25^2=625\)个SH了
-
运算开销:
Diffuse情况只需向量点乘向量,而Glossy情况下需要向量乘以矩阵
-
当Glossyness非常大(接近镜面反射)时,PRT无法解决
- 理论上可以用非常高阶的SH来描述,但是SH描述非常高频的东西效果并不好,可以使用其他基函数
- 当接近镜面反射时,其实能直接知道物体是如何反射到其他东西的,直接ray-tracing
Time Complexity
-
一般SH函数会用到3/4/5阶(也就是9/16/25个SH)
以下以4阶为例
-
Diffuse Rendering
两个长度为\(16\)的向量做点乘
-
Glossy Rendering
长度为\(16\)的向量乘以\(16\times16\)的矩阵
Interreflections and Caustics
-
Real-time Rendering中的物体材质
- Diffuse
- Specular 光线会完美往镜面反射方向反射
- Glossy 介于Diffuse和Specular之间
- 有时候说Specular也指Glossy
-
Transport Paths
可以使用一系列的表达式来描述一系列的路径是什么类型
- LE 光线从发出直接被看到 (Light Eye)
- LGE (Light Glossy Eye)
- L(D|G)*E 光线从出发打到Diffuse或Glossy物体后被看到 *表示0、1、2...次数
- LS*(D|G)*E caustics(焦散):光线打到Speuclar物体,被聚焦到Diffuse物体后被看到(LSDE)
所有任何\(Light\ transport\)的形式都可以分成Light和剩下的所有东西
因此在实际渲染时,只要采用PRT的思路,把Light和Light transport拆分后,无论Light transporty有多复杂,只要预计算了,在实际渲染时都非常简单(与light transport的复杂度无关)
改进工作
- 用别的基函数
- 预计算更多的项,比如预计算Lighting,预计算Visibility,BRDF等等,这样最终渲染时就不是两项相乘再积分,而是三项相乘再积分了
- PRT限制了场景得是静态的,有什么方法可以允许场景或材质一定程度上发生一些变化?
- 其他效果:半透明、头发等等
- 不进行预计算,而且通过近似获取解析解
最后,PRT非常难写,所以工业界用的不是特别多
More basis functions
Wavelet 小波
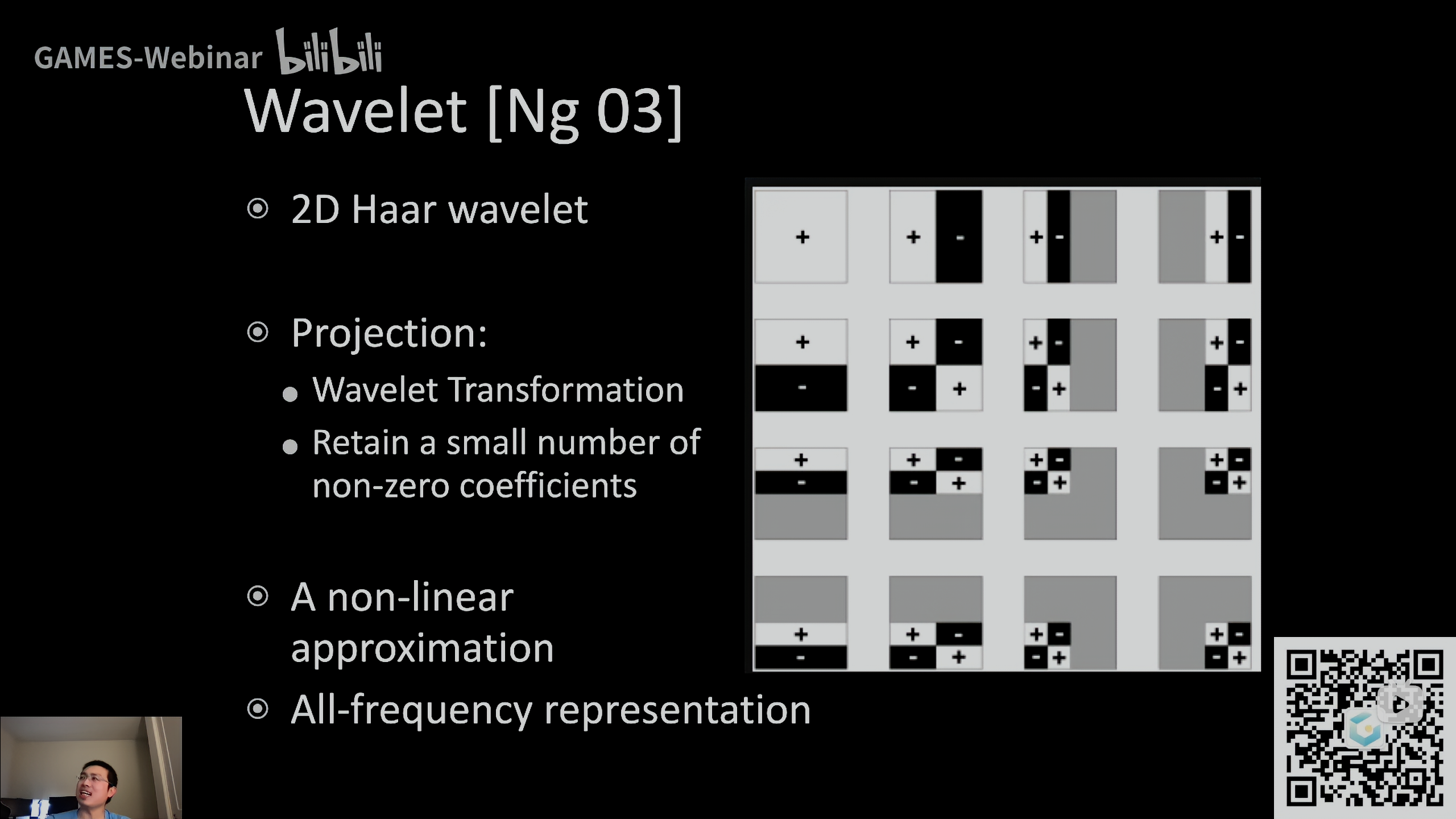
小波的定义域
小波是定义在图像块上的,而且不同小波的定义域不同,如图中第三列右半部分都没有,第三排下半部分都没有
小波也有很多种,这里说的是2D Haar wavelet,这种小波有明确界限
小波的压缩方式
将函数投影到小波基函数上,会发现大量的小波基函数的系数是接近0的,那么就取对应系数最大的多少个 (non-linear approximation)
与Spherical Harmonics相比,最大的好处是支持全频率的表示,可以表示低频,也可以表示高频
Non-linear Wavelet Light
既然小波是定义在平面上的,那么用小波来描述定义在球面上的函数就会出现一条缝,所以用Cube Map来描述这2D球面函数
Wavelet Transform 小波变换


首先对于任何一张图,将高频信息留在除左上方的三个格子,将低频信息留在左上方,再不断地重复这个操作,就可以得到最终结果了(类似四叉树),而高频部分绝大多数地方结果都是0
-
JPEG使用的是DCT(离散余弦变换),类似小波变换
-
JEPG2000使用的是Haar小波
小波的优缺点
-
对比Spherical Harmonics,小波可以渲染出更加高频的阴影,高频的阴影意味着将高频的Lighting信息描述下来了
-
但是小波存在一个非常严重的问题,小波不支持快速的旋转
Others
- Zonal Harmonics
- Spherical Gaussians (SG)
- 理论上上来说SG不应该叫基函数
- Piecewise Constant
![[转]高斯-牛顿算法](https://img-blog.csdn.net/20160609002742523)


![[转]OpenCV4.8 GPU版本CMake编译详细步骤 与CUDA代码演示](https://img2024.cnblogs.com/blog/494924/202409/494924-20240901123955342-1942084893.png)
![[图文直播]搭建Zfile私有网盘](https://img2023.cnblogs.com/blog/3485711/202409/3485711-20240901122652658-1117766162.png)