[笔记]Tarjan-编程知识

[笔记]Tarjan

news/2024/11/16 9:54:32/文章来源:https://www.cnblogs.com/Sinktank/p/18386301

Tarjan求强连通分量

定义

DFS树相关

我们对一个有向联通图进行DFS遍历，会得到一棵DFS树。

DFS树的形态是根据我们DFS的顺序来决定的，因此对一个有向联通图来说，它的DFS树可能有多个。我们把这棵树的边称作树边。

其他边我们分为\(3\)类：

前向边：从\(u\)到它dfs树上的祖先的边。
后向边：从\(u\)到它dfs树上的后代的边。
交叉边：除了前向边、后向边，剩下就是交叉边了。

如下图所示：

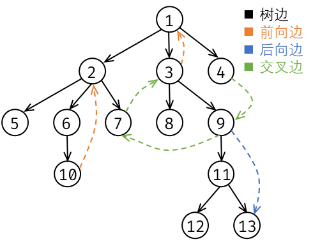
强连通分量

称一个有向图是强连通的，当且仅当任意两个节点可以互相到达。

强连通分量就是一个有向图的强连通子图。

上图的强连通分量找出来就是这样的：

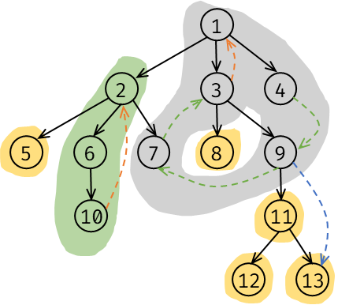
正片

Tarjan算法用一次DFS完成，用\(1\)个栈来存储当前遍历过的节点中，还没找到强连通分量的节点。

我们为节点\(i\)定义\(2\)个属性：

\(dfn[i]\)：节点\(i\)的时间戳，即\(i\)是第几个被搜索到的节点。
\(low[i]\)：节点\(i\)通过至多\(1\)条非树边，能到达的在栈中的节点的最小时间戳。

接下来任意选定\(1\)个节点开始DFS，遍历到的每个节点入栈，并初始化\(dfn[i]=low[i]\)，都为该节点被遍历的次序。对于节点\(u\)，枚举它能直接到达的节点\(i\)：

如果\(i\)未被访问：那么对\(i\)进行搜索；由于\(u\)能直接到达\(i\)，所以根据定义，\(low[u]=\min(low[u],low[i])\)。
如果\(i\)被访问过：
- 如果\(i\)在栈中：说明\(u\)通过一条非树边到达\(i\)，那么根据定义，\(low[u]=\min(low[u],dfn[i])\)。
- 如果\(i\)不在栈中：说明\(i\)所在的强连通分量已经被找到，所以什么也不用做。

如果完成节点\(u\)的搜索，发现\(dfn[u]=low[u]\)，则说明\(u\)是一个强连通分量中时间戳最小的，因此不断出栈直到\(u\)（包括\(u\)）为止，出栈的所有节点是一个强连通分量。

代码：

int low[N],dfn[N],tim;//tim是不断增加时间戳
bool vis[N];//vis[i]表示i是否在栈中
stack<int> st;
void tarjan(int x){low[x]=dfn[x]=++tim;st.push(x);vis[x]=1;for(auto i:G[x]){if(!dfn[i]){//没访问过tarjan(i);low[x]=min(low[x],low[i]);}else if(vis[i]){//访问过，且在栈中low[x]=min(low[x],dfn[i]);}}if(dfn[x]==low[x]){while(1){int t=st.top();st.pop();vis[t]=0;if(t==x) break;}}
}

然而只选定\(1\)个节点不一定能处理到所有节点，因此主函数中我们要这么写：

for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i);

一些问题&思考

\(\textbf{1.}\)主函数中循环的写法为什么是正确的？

首先可以发现，主函数中每完成一次搜索，栈都是空的，因为搜索过程中，如果\(i\)已经处理过了就什么都不做（情况2.2），所以强连通分量之间互不干扰，已经搜出的强连通分量，可以直接看作从图上被删掉。自然根节点的\(low\)不会得到更新，搜索结束栈会被清空，所以不会出现“处理了一半的强连通分量”。

\(\textbf{2.}\)为什么\(low\)的定义必须限制“最多经过\(1\)条非树边”，为什么是正确的？不加限制会影响正确性吗？

实际上如果不加限制的话，是没法递推的。如下图：

我们从节点\(1\)开始搜索，现在正在搜索节点\(3\)。\(3\)有一条连接\(2\)的边，如果\(low\)的定义不加限制，\(low[3]\)应该和\(low[2]\)取最小值。可是\(low[2]\)还没有求出来，它的值可能是\(1\)也可能是\(2\)，取决于搜索的顺序。这样子就有后效性了，是无法递推的。

接下来证明Tarjan算法的正确性，即“按顺序搜索，如果遇到\(low[i]=dfn[i]\)则不断出栈”是可行的。
假设现在完成了对子树\(u\)的搜索，现在有\(low[u]=dfn[u]\)，我们可以把除\(u\)以外的所有点分成\(5\)类：

没访问过的。
访问过，但现在不在栈中。
访问过，现在在栈中，\(u\)的上方。
访问过，现在在栈中，\(u\)的下方。

我们要证明的是“\(u\)和第\(3\)类节点构成一个强连通分量”。

即：证明\(u\)和第\(3\)类节点互相可达，而且与其他类型的节点不互相可达。

\(\bf{Type 1}\)：没访问过的：
我们需要证明此类节点和\(u\)不能互相到达。
- 既然\(u\)的子树已经搜索完了，那么还没有访问到的节点，就是从\(u\)走不到的节点了。
\(\bf{Type 2}\)：访问过，但现在不在栈中：
如果我们用“此类节点属于其他强连通分量”来解释，就算是循环论证了。我们仍然需要证明此类节点和\(u\)不能互相到达。
- 设该节点为\(v\)，则分类讨论一下：
  - 如果\(dfn[v]<dfn[u]\)，那么从\(v\)出发一定到不了\(u\)。我们假设\(v\)能到达\(u\)，又因为\(v\)比\(u\)先遍历到，所以\(v\)一定是\(u\)的祖先节点（思考一下，如果子树\(A\)比子树\(B\)先遍历到，那么一定不存在\(A\)到\(B\)的边），自然应该在栈中（\(u\)的下方），产生矛盾。
  - 如果\(dfn[v]>dfn[u]\)，那么从\(v\)出发一定到不了\(u\)。因为我们刚遍历完\(u\)的子树，所以时间戳比\(u\)大的都是\(u\)的后代，自然\(v\)也是。我们设\(v\)能到达的最早节点为\(w\)（留心定义，和\(low\)不太一样）：
    - 如果\(dfn[w]<dfn[u]\)，那么显然有\(low[u]<dfn[u]\)，与\(low[u]=dfn[u]\)矛盾。
      如果有点蒙，你可以想象\(v\)沿着\(low[v]\)一直往上跳，直到\(low[v]<dfn[u]\)为止，此时的\(v\)仍然是\(u\)的后代，而\(u\)又是\(low[v]\)所代表节点的后代。自然\(low[u]\)会更新为\(low[v]\)。
    - 如果\(dfn[w]>dfn[u]\)，那么\(v\)最远只能到\(u\)的后代\(w\)，所以到达不了\(u\)。
\(\bf{Type 3}\)：访问过，现在在栈中，\(\bf{u}\)的上方：
证明此类节点和\(u\)能互相到达。
- 这类节点因为是\(u\)的后代，所以\(u\)可以到达它们；反过来，这些节点可以到达\(u\)吗？是可以的。如果此类节点\(v\)能到达的最早节点是\(w\):
  - \(dfn[w]<dfn[u]\)，和\(\bf{2.2.1}\)情况类似，会出现矛盾。
  - \(dfn[w]>dfn[u]\)，和\(\bf{2.2.2}\)类似，那一定在\(u\)搜索完之前被出栈出去了，与“在栈中”矛盾。
  上面两种情况都不存在，因此所有\(v\)都能到达\(u\)。
\(\bf{Type 4}\)：访问过，现在在栈中，\(\bf{u}\)的下方：
证明此类节点不能和\(u\)互相到达。